Linked Liststo be viewed This presentation is intended

Linked Liststo be viewed This presentation is intended in slideshow mode. If you are reading this text, you are not in slide show mode. Hit the F 5 function key to enter slideshow mode.

Linked Lists § Introduction and Motivation § Linked Lists versus Linear Lists § Abstract Properties and Operations § Animation of a Dynamic Linear Structure Implemented as a Linked List § Building (Insertion Into) a Linked List: Simplest Case § Traversal and Traversal-Based Operations § Variations, Embellishments, and Elaborations § § Bi-directional Lists Circular Lists Headed Lists Summary MSJ-2

Motivation Both Real World Engineering and Pedagogical § Linked lists are the simplest of the fundamental computer science objects known as dynamically linked structures § They are dynamic in that their size can vary during execution as individual items are inserted into or removed from the list, like the list of students in CS 315, which can and usually does change after the semester starts as some students add the course and others drop it § Linked lists are extremely useful in and of themselves – e. g. , the CS 315 roster – and they provide the basis for even more interesting (both theoretically and practically) objects such as stacks, queues, and binary trees, the most beautiful data structures in the universe § Implementation of even the simplest of linked list operations requires careful thought, selection among multiple design alternatives, and excruciating care with the coding details – all skills that apprentice software engineers need to cultivate MSJ-3

Linked Lists and Linear Lists § Linked lists are one of two common implementations of a slightly more abstract concept known as a linear list (a one-dimensional array is the other implementation) § Unlike, for example, binary trees, the abstract properties of linear lists by themselves are not to me that fascinating; what makes them worth our study here is their tremendous real world utility and the importance of mastering their linked implementation alternatives that we’ll use throughout CS 315 (and that you’ll often use professionally later) § But I promised in my introduction to this course that we would begin our discussion of every data structure this semester with a discussion of its abstract properties so I’ll include them here for logical consistency – but I’ll be brief (for me ; -) MSJ-4

Abstract Properties of Linear Lists § Each item in the list except the first has a unique predecessor and each except the last has a unique successor George Washington John Adams Thomas Jefferson … George Bush Barack Obama The uniqueness of the predecessor/successor relationship means that the list can be laid out as illustrated above and is the reason that simple lists are often known as linear lists § A list may or may not be empty, but, in the abstract, there is no maximum size § Note that an array does have a maximum size, the one you declare, and, as far as C is concerned, its size is constant § This is a theme we’ll see again and again – an implementation of an abstract data structure may induce properties or limitations that the abstract structure itself does not have MSJ-5

Abstract Operations on Linear Lists § Traversal – visiting (e. g. , printing out) each item in the list; comes in two flavors: first-to-last and last-to-first § Search or find – determining whether a given item is present § Deletion – of a given item § Note that insertion can’t be defined without more information § There are many possible places where insertion could occur § In front of the front § Behind the last § Somewhere in the middle (where? ) § So a definition of “insertion” will require more knowledge about where and why; for linear lists, its behavior is not uniquely defined just from the linearity property MSJ-6

Abstract Operations on Linear Lists (cont’d) § Any abstract data structure has certain operations and characteristics defined even in the abstract, regardless of implementation § Whether or not a given application needs a given operation on some data structure is an engineering issue, not a theory of data structures one § As an engineer, you need to know what the properties and operations are so that you can pick an appropriate structure for your problem ─ it may have more than what you need, but it better not have less MSJ-7

Abstract Operations on Linear Lists (cont’d) For linear lists, the abstract properties and operations may seem pretty obvious and hence this discussion mostly unnecessary, but later this semester we’ll be dealing with data structures whose properties and operations are much less obvious and I want to start out doing things properly, i. e. , defining our structures in the abstract before moving to questions of implementation MSJ-8

Linked Lists § Introduction and Motivation § Linked Lists Versus Linear Lists § Abstract Properties and Operations § Animation of a Dynamic Linear Structure Implemented as a Linked List § Building (Insertion Into) a Linked List : Simplest Case § Traversal and Traversal-Based Operations § Variations, Embellishments, and Elaborations MSJ-9

Example of a Dynamically Linked Data Structure § Suppose we want to write a program that works with a set of numbers whose cardinality varies widely – perhaps a variable number of temporary data entry clerks input the numbers one at a time until they get tired and tell our program “no more”; we couldn’t know in advance how many clerks we would have available on any given day nor how many items any given clerk would actually enter in any given day § If our code declared too big of an array size, most of the time we'd be wasting most of it § But if we declared too small an array and filled it up, we couldn't keep going without major problems § A dynamic data structure whose size can increase one cell at a time whenever we want it to is what we need § A linked list implemented with pointers is an important technique for implementing such a dynamic data structure MSJ-10

Dynamically Growing a Linked List start 18 -2 When we get a number, we use malloc to dynamically obtain some storage 461 23 the list 314 space for it and link it into § And so on. . . § Notice that the structures in the list have no names; they § Thecan nextonly timebewe get a new we – names are part of accessed vianumber, some pointer again some new space and link theget communication fromfor theit programmer to the compiler; it in these to the objects, end of the growing above, are list not compiled objects; they are during program § Notecreated that thedynamically list elements are not simpleexecution, the compiler is long gone of some sort, integer cells but structures since each must have space for a pointer in it as well as the integer MSJ-11

Linked Lists § Introduction and Motivation § Building (Insertion Into) a Linked List: Simplest Case § Traversal and Traversal-Based Operations § Variations, Embellishments, and Elaborations MSJ-12

Example of Building a Linked List § The previous animation was designed for simplicity of imagery, to get us started visualizing the concept of a linked list § start pointed to the original (oldest) item in the list, new items being inserted to the right, at the far end of the list, after previous items; the list growing in the direction of its links start • • • older newer § Although the code for this version of insertion is simple enough, it’s not actually the very simplest version to code. § Insertion at the front of the list, new items being inserted before (to the left of) previous items is actually slightly simpler, so to keep our sample code as simple as possible, that’s what we’ll look at § Later, we’ll also look at why and how we might insert in the middle of the list rather than at one of the ends

Animation for the Code Example We’re About to Do § start will always point to the most recent item in the list, new items being inserted in front (to the left) of older items § And we’ll color code the various components of our structure so help us tell them apart § This is what we’ll code: integer pointer to our structure 0 start • • • MSJ-14

The Creation of a Linked List: § At this point we§have theused insertion of the Notecompleted that the & is normally to first element First Insertion into a previously empty list provide aninsert address to scanf for this in front of § Since we want to our LIST_ITEM §The Although this very firstnew time through insertion loop we could store the address the location ofpoints the storage the current start ofstill our list, we need to make our so new § The tempthe pointer actually into our list, too; but what? We'll also need afor temporary typedef struct list. Item returned byitem malloc directly start instead input onewith point to the currently at the i. e. , pointed We're done ituser's for now and won't tointo itfront, again until we pointer to refer hold the address { of temp, that won't work for any subsequent § And this statement, by setting start equal to by start create a new item returned by malloc for a new § As it happens, we could have left Note the use of sizeof(LIST_ITEM) int some. Integer; to temp makes start point to the same insertions cell before it's linked in to the list out the parentheses and just § At this point in our example here there aren't to make sure that malloc obtains theany items struct *next; as temp does, thus completing the § Our list. Item isplace the structure (set of items) pointed to by start; the written &temp->some. Integer, in the list so we just wind up setting temp->next to § On the next slide, we'll see that this logic we’re right amount space for us } LIST_ITEM; of the new LIST_ITEM into our list existenceinsertion and properties of that list are not affected by theit NULL (the current value of start) which is fine, writing here is general enough so that it actually but unless one remembers the atofthe very front ; *temp; , LIST_ITEM *start = NULL existence other “leftover” pointers those items works for allprecedence our insertions operator tables, indicates that this item is thepointing last itemtoinany theoflist, which it § This definition defines a recursive structure, also known as while (? ? ? )§ Note this statement and the one safe than sorry; and Iadd think will be –better when there's one item inbefore the list, as there § start, or whatever other name you choose in your code, §that Now let's look atonly the logic toitem a this a self-referential structure, since each of typealways { to be in exactly the right or theindone version herethe isjust easier to read is now this current example, itaorder is both thewould start and Without typedef, this line be to have the complete list; temp is that, “working” variable new LIST_ITEM into the list (for sizeof(LIST_ITEM)); temp malloc ? ? ? =§points contains a pointer to another item of the same type Note that we still need to put the * in front Notetothat name LIST_ITEM here needn't thethe list will wind uplist, looking rather strange! in any event, no? end of integer: the list, no? struct list. Item *start = –NULL; used help construct the but not part of the list itself a more printf( " Enter your " ); § The malloc will return the address for the of the variable name to indicate that what Also note that at this point we actually Now that our typedef is set up, we need to have any relationship to the name list. Item, §embedded We'll do name this inside of auser while loop § Here it's within just to makeexcept the rest which isacompletely equivalent, descriptive (i. e. , better) for ittypedef would have been § Anyway, now we'll ask the to provide scanf( " %d ", &(temp->some. Integer) ); we want to declare here is a pointer to aroom new memory just allocated to us have a completely valid linked list; it'sreadability declare a pointer to the start of the list, likeitems the one above, asitan far as theawe compiler isdidn’t concerned since don't know how many of the program little easier to read new. Item. For. Insertion, but I have for anything that possibly for integer value for our new list item temp->next = start; LIST_ITEM, not a LIST_ITEM itself, just empty at the moment wethese saw incharts the user simpler earlier the will animation want to add long on § We need to store that address in a pointer however, itwe seems good idea toand think about §which, Look§ at next line (when itatogets here ; -)user I'mthe sure you remember, isstore what start§=Stylistically, temp; Here's where want the variable somewhere or never be able make them somehow, and C is case §we First, we get some new how you'd write itthis if need there were no typedef we'd get ifrelated leftwe'll out the *to in front of the } input; and integer cell can be referenced use this new chunk of memory in the future sensitive, so all caps for typedef's is a memory for our new cell with our old name temp as temp->some. Integer, correct? § That's one of the major uses for a typedef, brevity and friend the function common convention (butmalloc not a requirement) start improved comprehensibility temp 37 MSJ-15

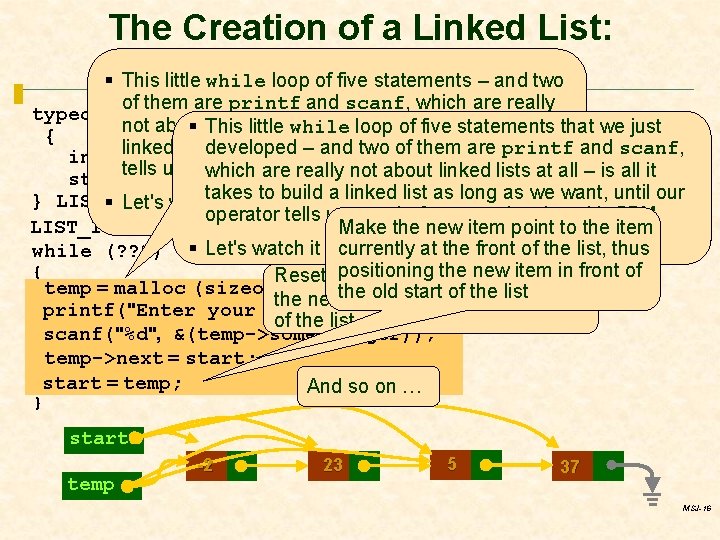
The Creation of a Linked List: More Insertions § This little while loop of five statements – and two of them are printf and scanf, which are really typedef struct list. Item not about linked lists at all loop – is all takes to build athat we just § This little while of itfive statements { linked list developed as long as –we want, our operator and two until of them are printf and scanf, int some. Integer; tellslist. Item us towhich quit, for 5 PM lists at all – is all it areexample, really notsince aboutit'slinked struct *next; takes to build a linked list as long as we want, until our } LIST_ITEM; § Let's watch it at work a few times operator tells us to quit, for example, since it's 5 PM ; *temp; LIST_ITEM *start = NULL, Make the new item point to the item work a few more times in our at the front of the list, loop thus while (? ? ? ) § Let's watch it atcurrently positioning the new { Reset the start pointer to item pointintofront of temp = malloc (sizeof(LIST_ITEM)); oldthat start theatlist the newthe item is of now the front printf("Enter your integer: "); of the list scanf("%d", &(temp->some. Integer)); temp->next = start; start = temp; And so on … } start temp -2 23 5 37 MSJ-16

Linked Lists § Introduction and Motivation § Building (Insertion Into) a Linked List : Simplest Case § Traversal and Traversal-Based Operations § Traversal § Search/Find § Deletion § Insertion into the middle (building an ordered list) § Variations, Embellishments, and Elaborations MSJ-17

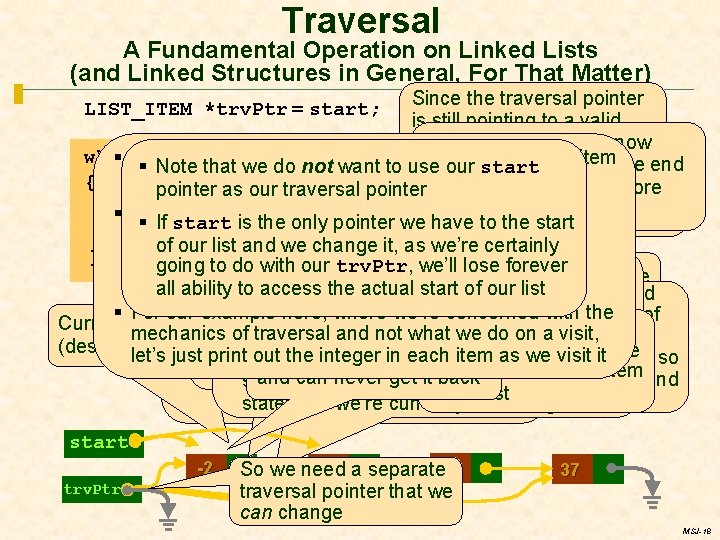
Traversal A Fundamental Operation on Linked Lists (and Linked Structures in General, For That Matter) Since the traversal pointer is. We’re still pointing a valid still nottodone with item, we’re done with And since trv. Ptr is nowto But first, not toyet know what the traversal … while (trv. Ptr != NULL) § To traverse data gotraversal through ityet one the …item NULL, we’ve reached end § Note thatawe do structure not want is toto use our start store in trv. Ptr, wethe have at a time, “visiting” each item in turn { of the list and are pointer asneed our traversal pointer totoevaluate therefore expression § We’ll a traversal pointer keep -2 23 5 37 printf( “ %d ” , trv. Ptr->some. Integer); done with the traversal trv. Ptr->next § The purpose of the visit is application dependent; track of wepointer currently in to the liststart § If start is where the only we are have the trv. Ptr = trv. Ptr->next; maybe, for example, we just want to add up all the of§our listinitialize and we itchange it, asof we’re certainly We’ll to the start the list, } values in the list, or maybe we’re searching to find here Since is a pointer, stored going to §do with next our trv. Ptr, we’ll what’s lose forever asvalue theaddress, name suggests, that’s …the so let’s visit the some since, specificis an which we represent in these all§ability to access the actual start of our list Thisstatement, statement’s syntax and Since this is an assignment usual starting point for doing much of current item … diagrams as an arrow, so the value of the So the current value of the expression § For our example here, where we’re concerned with the semantics are very typical of we’re going change the bit pattern anything withtoathe linked list ; -) Currently, trv. Ptr contains address of § Here’s the traversal code expression trv. Ptr->next is this arrow trv. Ptr->next is the bit pattern stored So the result of this mechanics ofstored traversal and not those what we oninanavigating visit, wedo use that’s in trv. Ptr (designates, or points to) this structure here, in the component named next of the tovisit advance We’ve lost access to -2 item let’s just print out the integer in each as is we itlet’s step … and then move on linked structures in general, so §statement It’s pretty simple; § So it is this address (arrow) that will be structure currently pointed to by trv. Ptr to the next item § Since stored trv. Ptr is a pointer, that means and can never get itthe back to the next let’s make sure we understand through it one in trv. Ptr by assignment our listof how it works we’re statement changing what points to executing theindetails we’reit currently LIST_ITEM *trv. Ptr = start; start -2 trv. Ptr 23 a separate 5 So we need traversal pointer that we can change 37 MSJ-18

Reminder On Interpreting and Using the Graphics of Linked Structures start -2 5 23 37 § The arrows portray the logical connectivity, or topology, of our structures, which is all that we really care about § The picture above emphasizes that this structure is a linear list (one item after another), other topologies are possible and used for other purposes; we’ll look at some later this semester • • • st ar t § The actual layout in memory need not look anything at all like our logical view, so long as the pointers still provide the correct topology; here, below, is a partial memory map showing how our linear list might actually be laid out in memory: 37 -2 5 23 • • • MSJ-19

Traversal Is a Fundamental Operation § It is important all by itself: E. g. , print out the list of all students enrolled in CS 315 § It is used at the beginning of several other key operations: § Search/find § Delete § Insert-in-order MSJ-20

Search/Find E. g. , Look Up a Phone Number Given a Last Name § Traverse the list, checking each item to see if it is the one being searched for, stopping either when we reach the searched for item or when we complete the traversal and have no more items to check § If we find what we were searching for, the search is said to be successful § If the traversal completes without finding the desired data, the search is unsuccessful; the target item is not present in the list MSJ-21

Delete a Specified Item § free is the systemdelete. Item(5); service call that returns memory to the OS, e. g. , free(del. Ptr); § As a programming matter, we should save the address of this some pointer variable (it’s currently in del. Ptr) § free is item thus in the opposite of malloc § High level § Maybe we’d to insert into a different structure after § Note thatpseudocode: we arewant freeing up theit memory that del. Ptr points we actually deleted del. Ptr it from this one – e. g. , after a student flunks to, not itself CS 315, remove student recordissues from the list let’s of current § There arethe some interesting here; look at § Search for the item to be deleted using the standard Science majors andpractice, then insert it into a list of § As a. Computer matter good programming everything anofexample search/traversal logicshould eventually be explicitly returned obtained via malloc Sociology majors § via Here’s the situation wea have traversed the list to the OS a free call – from as after part of program’s cleanup§ §Item 5 has been deleted the list Non trivial question: Justwere At the least, if we really all done with this item, andis successfully found the item to be– deleted § Ifhow the search unsuccessful, do nothing or maybe But do we very designate before-shutdown processing, if not before exactly how do weitself we’dwe want to return its still storage to it’s the operating system § Note that the item exists; thisreport cell that want to know what to set 5 it to: As far as the list itself is § Let’s say, for example, that it’s. We the item containing that what the item towith be deleted was not found designate the pointer we § But since we do an item after deleting it from a just not part of the linked list anymore: set to del. Ptr->next ? concerned, all want we need that we to delete we won’t need toisnow adjust? structure application dependent, this step in ? ? ? show = del. Ptr->next; item 23 points to item 37 to do to delete the item §? ? ? If the item here; to bewe’re deleted is found, with adjust pointers as = del. Ptr->next; our code only concerned the list theory and is to of adjust one pointer practice deletion necessary to remove it from the list start -2 23 5 37 del. Ptr MSJ-22

Reminder Item (cont’d) Delete a Specified the § In terms of code. Adjusting development, do the. Pointers general case first; in this case, that’s when item to be deleted is somewhere in the middle of the list delete. Item(5); delete. Item(2); § Then figure out if you need special cases – i. e. , places where the logic for generalmethod case won’t work the use of two Onethe standard involves traversal pointers: a leader a trailer, where § Typical special cases involveand working at the ends of the list trailer is always kept one item behind the leader § Insothis example, theleader general purpose logic works correctly to that when thedeletion item to code: be So here’s thefinds actual § Note that there will be a special case to handle the of the so very deleted, next is the that delete thethe lasttrailer’s item, but failspointer to delete the one first deletion item properly, first item inwe the list: trail->next = lead->next; here needed special case; sometimes must beonly adjusted to one actually do the deletion of the you’ll need /* Traverse/search toby find item to be deleted */ more, sometimes fewer; but when trying to figure out your item pointed to thethe leader § Designating the pointer to the item to be deleted algorithm, start with/*the generalfirst case item that is to be deleted */ if (lead == start) It is the (bypassed) will require some additional work start = start->next; § And start by drawing/annotating pictures showing which There areget two morelogic orwhen less approaches else §/* “Normal” deletion */ obvious pointers adjusted and to point to where trail->next = lead->next § Only then, when you’re sure you’ve got a workable algorithm, worry about translating it into code start § That’s 5 -2 known as separation 23 37 formal of concerns, a more name for doing one thing at a time trail lead del. Ptr MSJ-23

Another Way to Delete a Specified Item delete. Item(5); § Note that if the illustration here were the whole An alternative to the saved two pointer (leader/trailer) method is to only use a story, we never the address of this cell single, trailing pointer at the cost of slightly more complicated anywhere (it’s what used to be in del. Ptr->next), expressions in both “find-the-item-to-be-deleted” logic and the so now we can’tthe access this cell anymore actual deletion logic itself § We can’t even give it back to the OS, since the free call requires the address of!= the 5 cell while ( del. Ptr->some. Integer ) to ((del. Ptr->next)->some. Integer !=be 5) freed up, =and our code has no record of it anymore del. Ptr->next; Since the next component § Oopsy, we probably should have saved theaold del. Ptr->next = (del. Ptr->next)->next; And have, as before, iswe itself pointer type, the Here’s the loop condition we now … leaving us noalist, way to Since item, note: designated by del. Ptr->next, is itself structure that valuethis of del. Ptr->next somewhere deleted item 5 from the § C programming C evaluates multiple -> value of the expression want to use so that the loop stops designate the pointer del. Ptr->next designates has components, (del. Ptr->next)->some. Integer designates this … but whose next field is the that one It’s important to understand the Similarly, (del. Ptr->next)->next although, as before, the del. Ptr->next is an operators from left to right so the parentheses can be Here’s our old traversal loop, that with del. Ptr pointing to the item …next so here’s the pointer needed to be adjusted to the component of the to themeaning component, named some. Integer, so the value ofto the expression ofwill expressions like this that have be adjusted to designates the next field here … item itself continues to exist omitted from (del. Ptr->next)->some. Integer stops when del. Ptr points address/arrow that points to adjustment logic that does before the itemtotoby bedel. Ptr deleted … actually do the deletion item(del. Ptr->next)->some. Integer pointed is 5 multiple that have -> operators actually do the desired this, the next item of ourdeletion list item to be deleted … the del. Ptr->next actual deletion … § E. g. , evaluates to what we want and to me, is slightly easier to read; this is a rare case where knowing and taking advantage of start -2 23 and leaving 5 out 37 the C operator precedence rules unnecessary parentheses makes code more … by copying readable, not less … into this cell del. Ptr this value … MSJ-24

Still Need to Check for Special Cases if value. To. Be. Deleted) § As(start->some. Integer before, when we check for== problems we’ll see that the general case start = start->next; /* Delete logic doesn’t handle all possible casesthe very first item in the list */ else /* Traverse to find the value. To. Be. Deleted */ § To make this general case look truly general, let’s replace 5, the specific { value used in the last example, Here’s special casevalue. To. Be. Deleted our with the a more general del. Ptr = start; general logic can’t handle, deleting the first item in the list value. To. Be. Deleted) while ((del. Ptr->next)->some. Integer != 5) del. Ptr = del. Ptr->next; del. Ptr->next = (del. Ptr->next)->next; /* Do the deletion */ § And there’s no this way“single to initialize del. Ptr to approach anything earlier problem with trailing pointer” is that than sincethe }Onestart so that thistocode could the first item in the list‘if’ § Noteisthat this time the general case traversal is inside an del. Ptr initialized start, thecheck first item the traversal loop, above, statement whereas last time (separate leading and of trailing pointers) actually looks in for the value. To. Be. Deleted is actually the item Putting the ‘while’ loop one case an second § The result isgeneral thattraversal thiscase code, above, can’tasfind the item containing -2 And the same logic we used thelisttraversal logic was the same all and only the actual in the – can’t i. e. , itdelete starts looking atsolves 23, innot atcases 2 enclosing ‘if’ statement the problem and so it before correctly everything else deletion logichandles itself had the special case which resulted in the ‘if’ statement being inside the while loop § There’s no general pattern to 23 special cases; 5 the only firm start -2 37 rule to follow is that one should develop the general case logic first, then figure out what the special cases are (they vary from problem to problem) , then add logic for them wherever and however necessary del. Ptr MSJ-25

More Special Cases, Still Using Only § Note that we need to add a check to our traversal/search loop to keep us from advancing beyond the end of the list. Pointer and then trying One (Trailing) Traversal to de-reference a NULL pointer, which would cause our program if (start == NULL) /*List is empty */ to blowup printf(“Can’t delete from an empty list, loop dummy”); The search completed The search loop looks for § Also note that we are relying on the fact that the && operator else if (start->some. Integer == value. To. Be. Deleted) without the evervalue. To. Be. Deleted finding the is a § We should also deal with the /* case that the value. To. Be. Deleted isn’t in short-circuit operator to keep our code from trying to list evaluate value. To. Be. Deleted start = start->next; Delete first item from */ del. Ptr->next->some. Integer when del. Ptr->next is NULL our list at all, which comes in two flavors: else /* Traverse the list looking for the value. To. Be. Deleted */ { § The is empty Thelistempty list case The special case for deleting del. Ptr = start; /* Initialize the traversal pointer */ The search loop terminated it found thethe value. To. Be. Deleted thevalue. To. Be. Deleted first item in the list § The list isn’t empty butwhen doesn’t contain while (del. Ptr->next != example NULL) &&illustrated here, not 23), (that’s 5, in(this single trailing pointer (del. Ptr->next->some. Integer != value. To. Be. Deleted) § We didn’t check for these (leading and trailing) ) this line of code deletes it cases in the two pointer del. Ptr->next; /* Move to have next item */ code that we= developed earlier; we should if (del. Ptr->next == NULL) /* Fell off the end of the list */ § Maybe the same code can cover both cases here, maybe it can’t; we’ll printf(“Can’t find %d in the list”, value. To. Be. Deleted) have to check and see else /* The traversal loop found the item to be deleted */ § In any event, let’s look here at the complete code/*for using del. Ptr->next = (del. Ptr->next)->next; Do deletion the deletion */ only a} single (trailing) traversal pointer start -2 23 5 The code above covers all the bases del. Ptr 37 MSJ-26

Linked Lists § Introduction and Motivation § Building (Insertion Into) a Linked List : Simplest Case § Traversal and Traversal-Based Operations § Traversal § Search/Find § Deletion § Insertion into the middle (Building an Ordered List) § Variations, Embellishments, and Elaborations MSJ-27

Ordered Lists § In an ordered list, items are ordered on the basis of some data item, known as the key, as illustrated in the ascending list below § Traversal, search, and deletion are the same as we saw before; but insertion is different § The earlier (simpler) insertion animations only inserted at one end of the list § Now, to keep the list in order, we’ll usually need to insert into the middle, no? § Suppose we wish to insert a node with a key of 24 into the list below, how would you go about it? Here’s some pseudocode: § Traverse the list to find the place to insert the new item so as to preserve the ordering Adjust appropriate pointers to actually do the insertion We§ need to the insert the new 24 new. Item. For. Insertion 24 node before the 30 one start 5 10 30 37 MSJ-28

Linked Lists § Introduction and Motivation § Building (Insertion Into) a Linear Linked List § Traversal and Traversal-Based Operations § Variations, Embellishments, and Elaborations § Bi-directional lists, including fascinating (or at least important ; -) sidebars on: § Topology again § l-values, r-values, and how compilers really process an assignment operator; all of which are necessary to understand expressions like a->b->c->d->e = a->b->c->d->e § Circular Lists § Headed Lists § Summary MSJ-29

Bi-Directional Lists Since all we’re interested in is the list § Just as a mechanics, structure can have more than one integer I’m not going to bother making up or floating point component, if we find it useful other data items to be past of for ourwhatever list items problem we’re trying to solve, it can certainly have more than one pointer struct bi. Directional. List. Item { … struct bi. Directional. List. Item *previous, *next; }; § So here’s what a bidirectional list might look like: start § Note that here we used multiple (two, to be precise) pointers of the same type; since that’s all we need for a bidirectional list § More complex problems (not simply bidirectional lists) might require multiple pointers of multiple types § Later we’ll look at other topologies – multi-linked structures that are not linear (a bi-directional list is still linear) such as orthogonal lists (for sparse matrices) or binary trees, the most beautiful data structures in the universe MSJ-30

Benefits for Bi-Directional Lists § It makes deletion a lot cleaner (neither of our two previous deletion algorithms was exactly elegant, were they? ) § After we find the item to be deleted, we don’t need leading or trailing pointers to help with the deletion delete(D) start A B C D E del. Ptr § Insertion into an ordered list is simplified, too, much as deletion is § Traversal in reverse order becomes possible; without a great deal of difficulty, it isn’t possible with a one directional list i. Is that important? It depends; some applications need to be able to traverse in both directions, some don’t ii. Your job, as an engineer, is to know the capabilities, plusses, and minuses of each of the tools/techniques in the standard armamentarium MSJ-31

Sidebar: Programmers and Topologies § It’s up to you, the programmer, to insure that you set up the pointers so that your lists have the desired topologic properties – e. g. , bidirectional linearity § If you wanted to, you could use the struct bi. Directional. List. Item that we defined on the last slide to make a linked thingy that looked like so: start A B C D E I can’t imagine why anyone would want to create a monstrosity like that (although some of you will probably manage something like it the first few times you try to create a bidirectional linear list ; -) but each item in the monster thingy would still be a struct bi. Directional. List. Item; only the connection topology would be different § C provides features to support pointers and structures, lists are up to you; there are languages that directly support lists and basic list operations (LISP, for example), but neither C nor any of its descendants are among them: the topologic properties of linked structures are up to the programmer MSJ-32

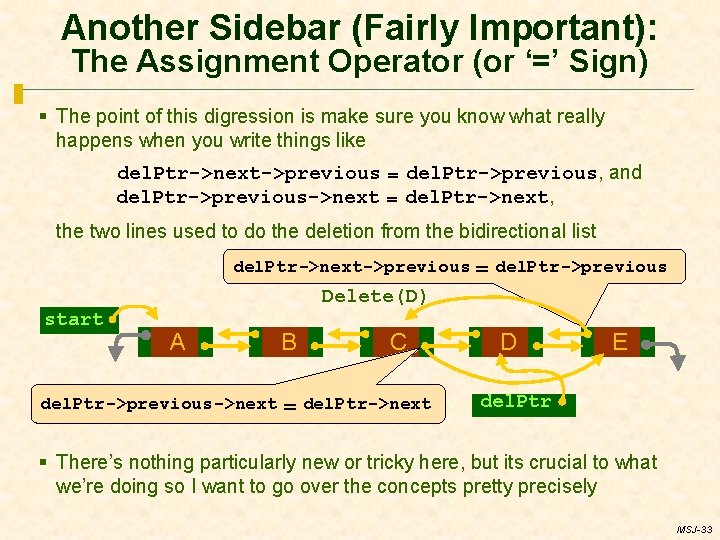
Another Sidebar (Fairly Important): The Assignment Operator (or ‘=’ Sign) § The point of this digression is make sure you know what really happens when you write things like del. Ptr->next->previous = del. Ptr->previous, and del. Ptr->previous->next = del. Ptr->next, the two lines used to do the deletion from the bidirectional list del. Ptr->next->previous = del. Ptr->previous Delete(D) start A B C del. Ptr->previous->next = del. Ptr->next D E del. Ptr § There’s nothing particularly new or tricky here, but its crucial to what we’re doing so I want to go over the concepts pretty precisely MSJ-33

Another Sidebar: The Assignment Operator In More Detail del. Ptr->next->previous = del. Ptr->previous The compiler must do three things for an assignment (=) 1. For the left side: a) Figure out the type of the value of the expression to the left of the = sign (e. g. , del. Ptr->next->previous); it must be an address value (pointer type) or the expression won’t compile b) Generate the code to evaluate that expression in real time when the assignment is executed 2. For the right side: a) Figure out the type of the value for the expression to the right of the = sign; it must be a type that’s legal for the address from the left-side expression to contain (e. g. , del. Ptr->previous = 3. 1416*diameter won’t compile) b) Generate the code to evaluate that expression in real time when the assignment is executed 3. Generate the code to store (assign) the computed value from the right hand expression in the memory location whose address will be computed by the code generated for the expression on the left side MSJ-34

The Problem with an Overly Simplistic View of the Assignment Operator (cont’d) § But given, for example, the declarations int x, y; if the assignment operation looks like x = y+2, the compiler would seem to have a problem: As far as we know so far, the type of a simple variable, like x, in an expression is the type the variable was declared as, int, in this case § But when we look more formally at the details, as we just did, the assignment operator requires the expression on the left to be an address type, not an integer MSJ-35

The Solution So here’s the compiler’s real logic: § Ordinarily, the value of a simple variable name like x is what we expect, i. e. , the value stored there and the type of that value is the type the variable was declared as § But, if the next operator to the right is an assignment operator*, the value of the variable name is the address of the variable and the type of that value/expression is the correct pointer type – e. g. , an integer pointer if x is an integer * Not just =, but +=, -=, *=, /=, %=, &&=, ^^=, etc; several of these are used rarely, if ever, but the compiler allows them and they are assignments MSJ-36

The Exception in Evaluating the Assignment Operator (cont’d) § To continue being technically precise, a simple variable name is thus overloaded in C, as in most modern imperative languages: It can be evaluated by the compiler to one of two completely different values (bit patterns) depending on where it is in a larger expression § To the immediate left of an assignment operator, its value is its address; elsewhere, it’s the bit pattern stored at that address (unless we explicitly use the & operator to ask for its address) § The two different possible values for the same variable name are referred to as its l-value and its r-value § The l- (or left) value being the address § The r- (or right) value being the bit pattern stored there § Which value the compiler chooses to use depends on where the variable name is, if it’s in an assignment statement MSJ-37

Sidebar: Assignment Evaluation (cont’d) The evaluation of an expression like del. Ptr->next->previous = del. Ptr->previous has the same issue and the same resolution Because it’s to the right of the = sign, Because it’s to the left of the assignment the value operator, the value of this expression will be the bit pattern stored in the cell designated be the address of the cell designated by the expression del. Ptr->previous del. Ptr->next->previous, namely the address of the cell for the component named previous of the structure pointed to by del. Ptr->next 5 10 15 Because both expressions are the same type, struct bi. Directional. List. Item *, or pointer to a struct bi. Directional. List. Item, the compiler is happy to generate the code to do the evaluations and make the assignment del. Ptr MSJ-38

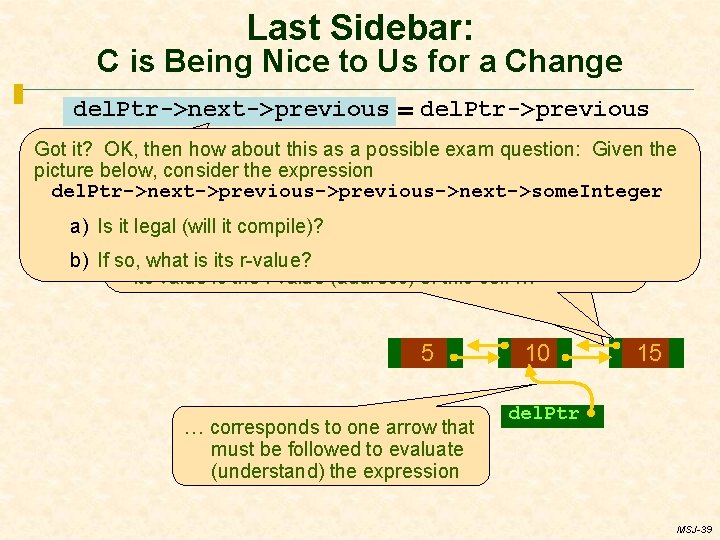
Last Sidebar: C is Being Nice to Us for a Change del. Ptr->next->previous = del. Ptr->previous Got it? OK, then how about this as a possible exam question: Given the del. Ptr->next->previous->next->some. Integer picture below, consider the expression, expression Each here … § -> Theoperator highlighted above, is designating the del. Ptr->next->previous->next->some. Integer I can’t imagine needing toexpression write such an expression, we’re … but if ever the highlighted above were notusually to the left of an component cell named previous in the structure Note the lovelyto (and hardly coincidental) correspondence between theto, working “closer” some named pointer (e. g. , del. Ptr), butr-value, if we need assignment operator, it would be evaluated to its pointed to by the highlighted arrows in this picture a) Is it C legal (will itpictures compile)? and the to understand the semantics since the typewe of need atoprevious is a pointer type, Csyntax allows of itwhich, and you now know how decipher itcell (congratulations ; -) is §the If what the expression is on thecell, left of an = sign, as it is here, address some other b) If so, is itsofr-value? its value is the l-value (address) of this cell … 5 … corresponds to one arrow that must be followed to evaluate (understand) the expression 10 15 del. Ptr MSJ-39

Linked Lists § Introduction and Motivation § Building (Insertion Into) a Linear Linked List § Traversal and Traversal-Based Operations § Variations, Embellishments, and Elaborations § Bi-directional Lists § § Circular Lists Headed Lists § Summary MSJ-40

Circular Lists a. Ptr. To. The. List An empty Andawhat linelist of to be circular list § What’s this? § Note that many authors (but not all) consider circular you each item merely an implementation technique for acode linearcould list, since § Thisand is the general case illustrated write to achieve it? here still has a unique predecessor a unique successor § There are ittwo special § The successor of an item is the item points to cases, one pretty § Not as ubiquitous as linear lists, but still usefulone not normal for linked listsquite in general, § The predecessor of an item is the one that points to it § Often used in operating systems – which we’ll explore in a § If, as shown here, the list is implemented uni-directionally, it won’t bit more detail in CS 420, e. g. : have pointers to predecessors, but that’s an implementation issue, not § Round robin scheduling a topological one; i. e. – the property that each node has a unique predecessor and amemory unique management successor is the topological, § Contiguous withabstract, a first fit or allocation policy property, known as linearity, regardless of whether or not the underlying implementation is uni- or bi-directional (or circular) MSJ-41

Linked Lists § Introduction and Motivation § Building (Insertion Into) a Linear Linked List § Traversal and Traversal-Based Operations § Variations, Embellishments, and Elaborations § Ordered lists § Bi-directional lists § Circular lists § Headed lists § Basic Concept § Example: Sparse Matrices § Summary MSJ-42

Headed Lists A. k. a. Lists With Sentinels § Anyway, the motivation for node) all this is stuff I hope, become that § A list header (a. k. a sentinel anwill, item § For our simple example, here’s a listin is a tolinked containlist only much clearer when we look at orthogonal lists to represent positive integers, but for this example, assume we also § Issparse the first item in the list (the head of the list) matrices, coming up next need to keep track of the length of the list for some reason § May not be deleted § It (sparse matrices) really is a pretty solution to an § Rather than declaring a separate variable for length, § Has some special important problem(application specific) semantics or meaning store the length in a node, but make ititnegative associated with some value in sentinel some field that identifies a sentinel … and the sentinel must be created dynamically Sometimes, the header is a declared node that Note the difference: Here, start is a declared so as tothe ensure that the header (sentinel) is Inot mistaken §(header) Remind me to─bring in and show you a fairly good textbook node examples will make this clearer, hope; bear Whereas here, start is and any deletion algorithm must be sure not starts the list, all other list nodes being created variable, but is a simple pointer not a structure … whom I forit. Computer an ordinary (positive) node (Gollmann, Security), where the author, with me normally to later delete it by accident a declared structure … otherwise mostly(i. e. , like, dynamically, states that a during certainexecution) implementation of a key in computer security can’tsome be used § Headed listsdata arestructure very useful and very common; problems in most cases because there’s no good, general solution to cannot easily with be solved any of other way a problem one aspect the implementation start § Bullshit you’ll know to 2 and solveimportant that problem after 52 a when few we § We’ll see-4 a–particularly lovely 78 example 17 how here lookmore at ancharts implementation of sparse matrices via orthogonal lists, but let’s start with a simpler example MSJ-43

Linked Lists § Introduction and Motivation § Building (Insertion Into) a Linear Linked List § Traversal and Traversal-Based Operations § Variations, Embellishments, and Elaborations § Ordered Lists § Bi-directional Lists § Circular Lists § Headed Lists § Basic Concept § Example: Sparse Matrices § Summary MSJ-44

Introduction and Motivation for Sparse Matrices § Although sparse matrices themselves are interesting and important objects, they don’t really belong here since they’re not linear lists § But they are built from linear lists and what interests us here is that the lists must be headed or we can’t get this sparse matrix structure to do what we need to § So looking at sparse matrices will give us a chance to see what drives the need for headed lists and how we work with them MSJ-45

A Multi-Linked Structures Example: Orthogonal Lists for Sparse Matrices § A sparse matrix is one where the majority of the entries in the matrix are 0 § Economists, for example, might want to keep track of the extent to which changes in the price of one commodity, product, or service (CPS) are correlated with changes in others § They prepare a complete list of CPS’s, possibly millions of entries long for a large national economy, then make a square matrix M, where each entry 0 ≤ mi, j ≤ 1 is the correlation coefficient between CPSi and CPSj § But the vast majority of the mi, j are all 0; I mean, how much do you think the price of steel correlates with the price of, for example, bubble gum? MSJ-46

A Multi-Linked Structures Example: Orthogonal Lists for Sparse Matrices (cont’d) § The natural representation of a matrix in a programming language like C is obviously a 2 -dimensional array § But if there were a million commodities, the array would have a trillion entries; if most of them were 0, that would be filling a lot of memory with zeroes; that seems wasteful § Very few modern systems will let you use a 106 x 106 array in any event § Even if such a declaration compiled, it would probably blow up in execution (that’s what happens on prclab) MSJ-47

A Multi-Linked Structures Example: Orthogonal Lists for Sparse Matrices (cont’d) § What we want is some other data structure (not an array) that just stores the non-zero elements of M § To find the value of some mi, j, we search the structure; if the search is successful, we know the (non-zero) value of mi, j, if the search is unsuccessful, we know its value is 0 § One implementation technique for sparse matrices involves what are called orthogonal lists MSJ-48

A Multi-Linked Structures Example: Orthogonal Lists for Sparse Matrices (cont’d) § Here’s a diagram of what each member of this sparse matrix structure* would look like: mi, j i next. In. Col. Ptr j next. In. Row. Ptr i and j are commodity numbers mi, j is the correlation coefficient between commodity i and commodity j § Each item is a member of two separate lists § All the non-zero items in row i form a single ordered list, ordered by j (their column number), linked by their next. In. Row. Ptr § All the non-zero items in column j form a single ordered list, ordered by i (their row number), linked by their next. In. Col. Ptr * The term structure is overloaded here. The sparse matrix is an example of the sort of theoretic object called a data structure that we study in computer science, particularly in CS 315. As an implementation matter, each element of the sparse matrix will be a structure in the C programming sense, (Many other languages don’t use the word “structure” this way; Ada, for example, calls such things “records”. ) Anyway, the figure, above, is a pictorial representation of the C structure that would comprise one element of a sparse matrix; the next slide illustrates how such elements fit together to make a sparse matrix MSJ-49

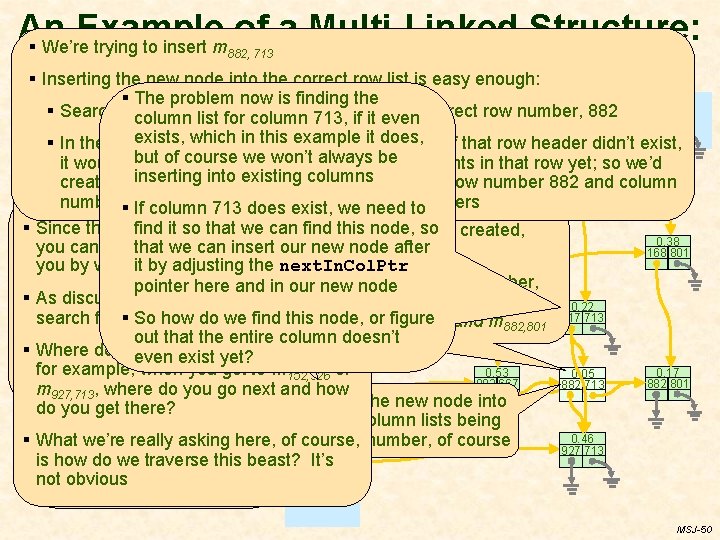
An Example of a Multi-Linked Structure: § We’re trying to insert m Orthogonal Lists for Sparse Matrices (cont’d) § Inserting the new node into the correct row list is easy enough: 882, 713 § The problem now is finding the - correct row - number, - 882 - to find the § Search the column row headers column listoffor column 713, -1 326 -1 667 -1 713 -1 801 -1 -1 if it even start. Of. The. Matrix exists, here, whichrow in this it does, but if that row header didn’t exist, § In the example 882 example already exists; but ofthat course won’t be elements in that row yet; so we’d it would mean therewe were noalways non-zero 0. 31 existing columns § Assume, example, that you wish create for theinserting new rowinto by inserting a to new node 152 -1 152 with 326 row number 882 and column know the value of m 56, 492 number of. If -1 into the ordered column of row to headers OK, things are going § column 713 does exist, we need Now the search logic is easy: § §§The answer is to add a row of column One answer could be to pretty so far; we can it so that this node, soor created, § Since thiswell data structure iswe notcan an find array, § find Once the correct row header is found headers to our structure search the entire matrix, 0. 62 0. 38 §you the column of row search this structure to that we can insert our new node after can’t simply ask C to retrieve it for insert mnow into that row 168 -1 168 667 §Traverse So here’s an illustration of a (very!) 168 801 which we can do 882, 713 headers by following the §you Then, after we insert the new node it by adjusting the next. In. Col. Ptr find out if m is in it by writing m[56][492] i, j x 1000 sparse matrix having that we 1000 added the § The solution here is torow add a in next. In. Col. Ptr § Since the lists are by column number, into the correct row list by searching pointer here and our ordered new node only 7 non-zero elements in it: column of row headers, §the How about insertion? column of row headers § As discussed earlier, your code has to the new node, m , , in column of row headers, we can 0. 22 - this example, must be 882, 713 m , m , m looking for entries that §search Each time you move down to 152, 326 168, 667 168, 801 617, 713 617 713 Let’s try inserting m 617 -1 § So how do we find this node, or figure for it inserted between 882, 713 then search the row of columnthe nodes for m 882, 667 and m 882, 801 m , and m § The column is an ordered the column number ahave new row, traverse it by 882, 667 882, 801 927, 713 out that the entire column headers for the correct column (713 indoesn’t linked list, ordered by row #, § Where do you start? And what happens, we wantthe following next. In. Row. Ptr even exist yet? this case), creating a new column if § Not very realistic, but it makes the linked by the next. In. Col. Ptr for example, when you get to m 152, 326 0. 17 0. 53 - or 0. 05 before moving down to the necessary … artwork here a lot easier and it will 882 801 882 667 882 -1 § But that seems awfully 882 713 mnext , where do you go next and how row ? still show the key issues we’ll have §do A 927, 713 row of sparse matrix …toand then insert the new node into inefficient; there’s got you getour there? to deal with will a row header in its this column list, column lists being behave a better way 0. 46 row number, of course 0. 46 column if and onlyasking if the here, ordered by § What we’re really of course, 927 -1 927 713 haswe attraverse least onethis nonismatrix how do beast? It’s zero value in the row not obvious MSJ-50

Here is the Complete Algorithm (Pseudocode) for the Insertion of mi, j start § Create the node for mi, j § Row insertion: § Search the column of row headers to find the header for row i § If row i does not yet exist, create a header node for row i and insert it into the column of row headers § Insert the mi, j node into row i § Column insertion: § Search the row of column headers to find the header for column j Note that in this particular problem (insertion into a sparse matrix), the § If order column j does not create lists a header node you for column of insertion intoyet rowexist, and column is irrelevant; could doj and the column insertion first, followed by the row insertion, or the row insert it into the row of column headers insertion first followed by the column insertion; there’s no ultimate § Insert the msince j are independent of one another i, j node difference, theinto two column operations MSJ-51

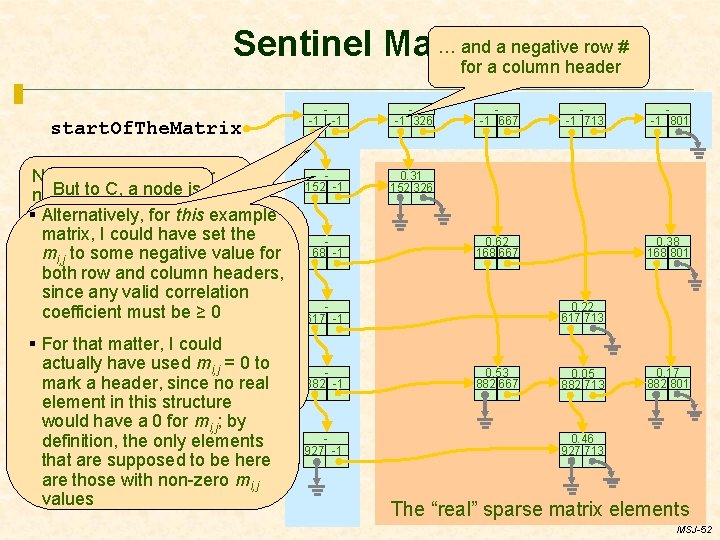
… and a negative row # Sentinel Marks for a column header start. Of. The. Matrix Note that these header But to a node is of nodes are. C, not elements asparse node ismatrix a node the §the Alternatively, for from this example § The sentinel mark is mathematical standpoint matrix, I could have setsome the attribute of some value forfor mi, j to some negative value some data in the node both row anditem column headers, that’s “special” and Insince this example far, so ourcan be any validsocorrelation used to haven’t identify a node algorithms actually coefficient must be ≥ 0 as a sentinel or header rather than needed to identify sentinel a node containing real data § For that I could nodes, butmatter, let’s complicate our actually have mi, j = 0 to life a little. I bit ; -) used §mark Here, used a negative a header, since no real column # this for astructure row header … element in would have a 0 for mi, j; by definition, the only elements that are supposed to be here are those with non-zero mi, j values -1 -1 326 152 -1 0. 31 152 326 -1 - 168 -1 -1 667 0. 62 168 667 927 -1 -1 801 0. 38 168 801 0. 22 617 713 617 -1 882 -1 -1 713 0. 53 882 667 0. 05 882 713 0. 17 882 801 0. 46 927 713 The “real” sparse matrix elements MSJ-52

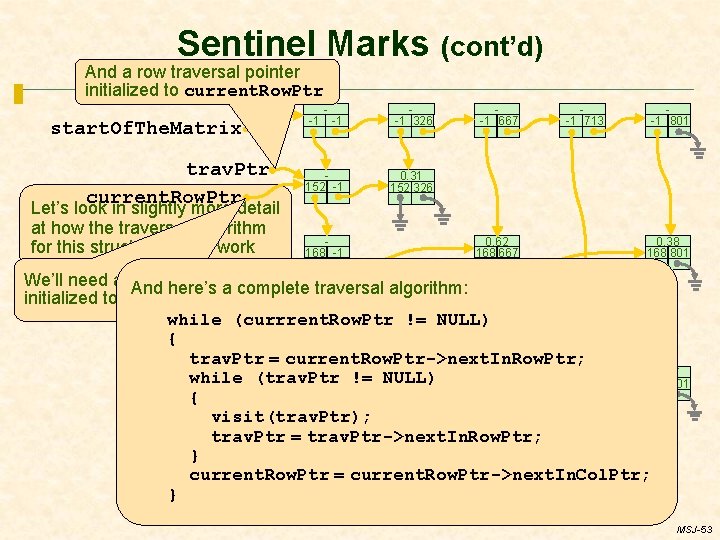
Sentinel Marks (cont’d) And a row traversal pointer initialized to current. Row. Ptr start. Of. The. Matrix trav. Ptr current. Row. Ptr Let’s look in slightly more detail at how the traversal algorithm for this structure would work -1 -1 326 152 -1 0. 31 152 326 -1 - 168 -1 -1 667 0. 62 168 667 -1 713 -1 801 0. 38 168 801 We’ll need a pointer to the current row being traversed, And here’s a complete traversal algorithm: initialized to start. Of. The. Matrix->next. In. Col. Ptr 0. 22 617 713 617 -1 while (currrent. Row. Ptr != NULL) { trav. Ptr = current. Row. Ptr->next. In. Row. Ptr; 0. 17 0. 53 0. 05 while (trav. Ptr 882 801 882 667 882 -1 != NULL) 882 713 { visit(trav. Ptr); trav. Ptr = trav. Ptr->next. In. Row. Ptr; 0. 46 927 -1 927 713 } current. Row. Ptr = current. Row. Ptr->next. In. Col. Ptr; } MSJ-53

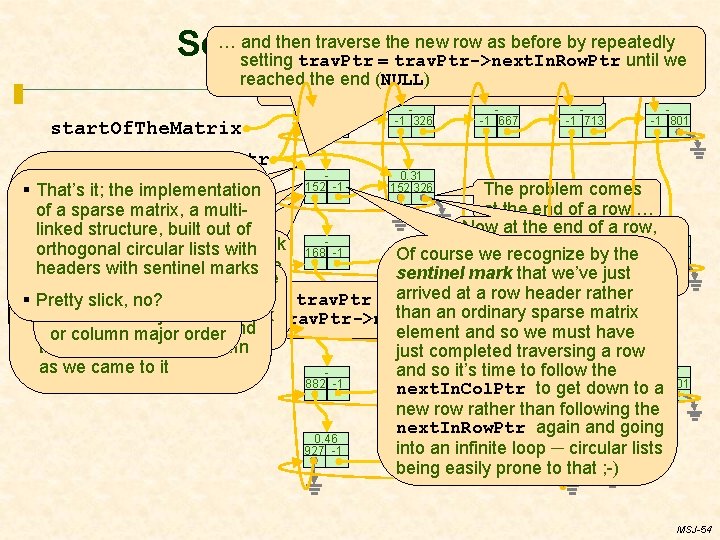
… and then traverse the new(cont’d) row as before by repeatedly Sentinel Marks setting trav. Ptr = trav. Ptr->next. In. Row. Ptr until we reached thefrom end the (NULL) Starting start. Of. The. Matrix… start. Of. The. Matrix -1 -1 326 -1 667 -1 713 -1 801 trav. Ptr 0. 31 § We already saw the row 152 -1 152 326 The problem comes § That’s it; the implementation Mosttraversal: implementations major We at the end of a row … of a… sparse matrix, a multitaking trav. Ptr would probably traversed the column ofright Now at the end of a row, linked structure, built out of back to where we circularize the column row headers and traversed 0. 62 0. 38 …orthogonal we need tocircular get trav. Ptr back 168 -1 the normal row traversal lists with 168 667 168 801 Of course we recognize by the need itcan towe be so that lists new as well as the row each row came to to here so we move down movement follows this headers with sentinel marks sentinel mark that we’ve just No sweat; let’s just we can move down lists, so that the matrix Now let’s do it with only a single next. In. Row. Ptr pointer… the next row by following the §traversal To do to abe column major arrived at a row header rather circularize the row lists! the next row could traversed in pointer ‒ no separate …slick, we could certainly move trav. Ptr down to a new row § Pretty no? traverse next. In. Col. Ptr; but wethe have 0. 22 traversal, we’d than an ordinary sparse matrix either row major order current. Row. Ptr to keep track 617 713 617 -1 by setting trav. Ptr = trav. Ptr->next. In. Col. Ptr … no way to get back here ofrow column headers and element and so we must have or column order ofrow what ismajor being traversed traverse each new column just completed traversing a row as we came to it and so it’s time 0. 17 0. 53 to follow 0. 05 the 882 801 882 667 882 -1 882 713 next. In. Col. Ptr to get down to a new row rather than following the next. In. Row. Ptr again and going 0. 46 into an infinite loop ─927 circular lists 927 -1 713 being easily prone to that ; -) MSJ-54

Summary of the Sparse Matrix § The sparse matrix implementation we just saw built a multilinked structure out of orthogonal circular headed lists § The sparse matrix is our first, it surely will not be our last, example of a multi-linked structure, one where each element has more than one pointer component § This is a theme we will see over and over again in CS 315: complex data structures being built up out of simpler data structures which in turn are built out of simpler data structures until we eventually get to something the language itself supports (pointers, in this example) MSJ-55

Summary of the Sparse Matrix (cont’d) § There are multi-linked structure like (yes!) binary trees where the linked elements are not organized into linear lists, but let’s leave that for another day (month, actually ; -) § The reason I put this sparse matrix problem here rather than waiting until later in this course has less to do with multilinked structures, although it is a great example, than that the sparse matrix is a pretty example (well, I think it’s pretty ; -) of an important real world problem that uses linked lists and that can’t be done without making those lists headed lists § The circularity was added mostly just to torture you – but it did eliminate the need for a separate named pointer to the current row, hardly worth the effort in this case, but under other circumstances, circularity can be more important MSJ-56

Linked Lists § Introduction and Motivation § Building (Insertion Into) a Linear Linked List § Traversal and Traversal-Based Operations § Variations, Embellishments, and Elaborations § § Ordered Lists Bi-directional Lists Circular Lists Headed Lists § Summary MSJ-57

Linear List Variants and Embellishments: Summing It All Up § You can mix and match all the linked list variants discussed here as your application requires; they are completely independent and every possible combination – e. g. , unordered circular unidirectional with a header, bidirectional with a header but not circular, ordered circular no header, etc – has been used for some problem or other § Your job, as always, is to know what techniques are available (that’s where Gollmann slipped up) and which are called for by what types of problems § Sometimes it’s obvious – if you need to print out ordered lists both forward and backward, bi-directional lists are clearly the way to go § Sometimes it’s not – which is why there’s more to good software engineering than merely being a good code-slinger MSJ-58