Linked Lists 2004 Goodrich Tamassia Linked Lists 1

Linked Lists © 2004 Goodrich, Tamassia Linked Lists 1

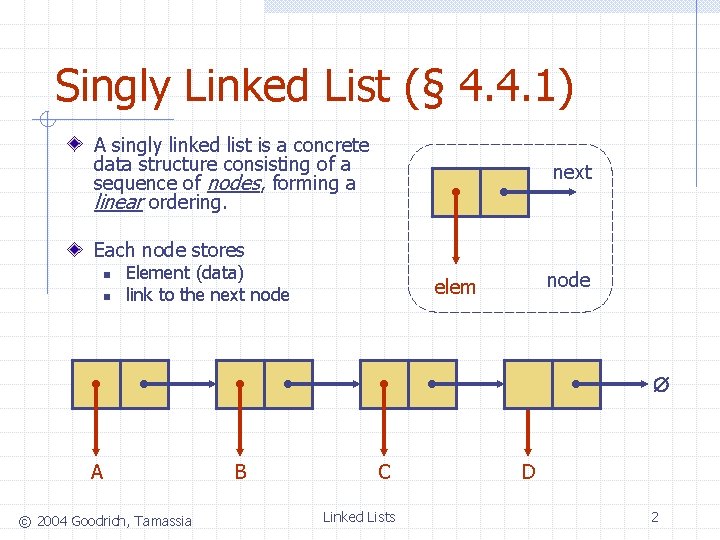
Singly Linked List (§ 4. 4. 1) A singly linked list is a concrete data structure consisting of a sequence of nodes, forming a linear ordering. next Each node stores n n Element (data) link to the next node elem A © 2004 Goodrich, Tamassia B C Linked Lists D 2

Empty Linked List An empty linked list is defined by: Head = Tail = Null List with Single Node Head = Tail ≠Null Head Tail © 2004 Goodrich, Tamassia Linked Lists 3

The Node Class for List Nodes public class Node { // Instance variables: private Object element; private Node next; /** Creates a node with null references to its element and next node. */ public Node() { this(null, null); } /** Creates a node with the given element and next node. */ public Node(Object e, Node n) { element = e; next = n; } // Accessor methods: public Object get. Element() { return element; } public Node get. Next() { return next; } // Modifier methods: public void set. Element(Object new. Elem) { element = new. Elem; } public void set. Next(Node new. Next) { next = new. Next; } } © 2004 Goodrich, Tamassia Linked Lists 4

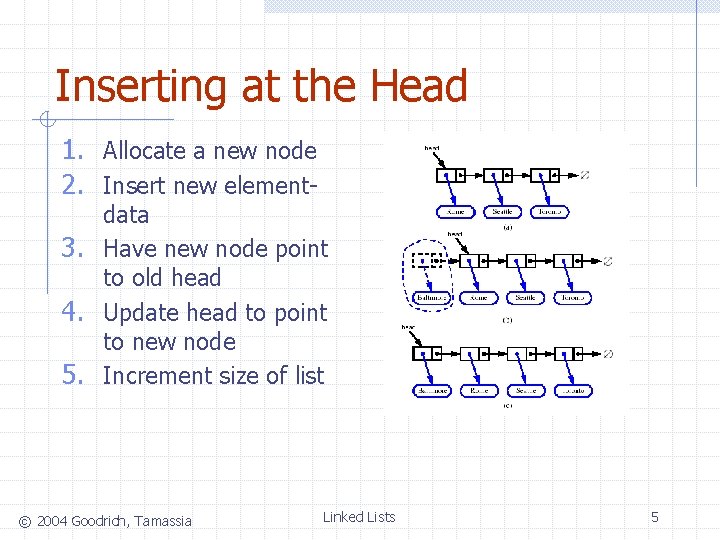
Inserting at the Head 1. Allocate a new node 2. Insert new element- data 3. Have new node point to old head 4. Update head to point to new node 5. Increment size of list © 2004 Goodrich, Tamassia Linked Lists 5

Algorithm for Inserting at Head new (T); T. data = A; T. next = Head; If (Head = Null) Head = T; © 2004 Goodrich, Tamassia //Create a new Node // store element data //new node points to old Head node then Tail = T // we have a single node-list // Update Head to point to the new node Linked Lists 6

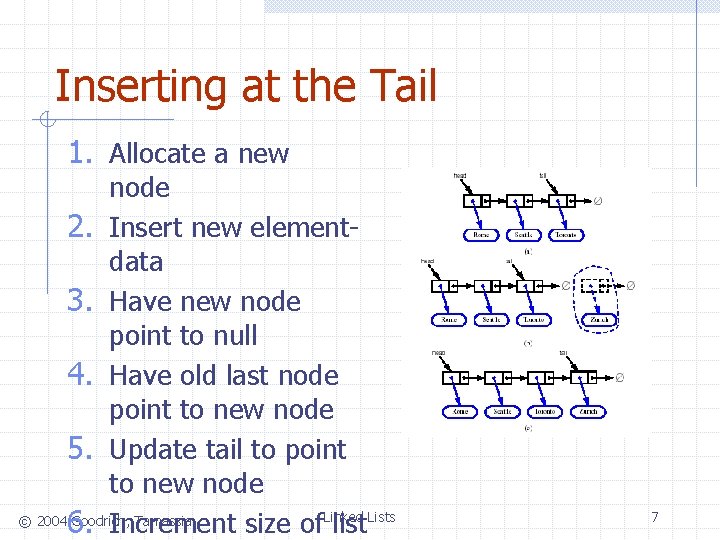
Inserting at the Tail 1. Allocate a new node 2. Insert new elementdata 3. Have new node point to null 4. Have old last node point to new node 5. Update tail to point to new node © 2004 Goodrich, Tamassia 6. Increment size of. Linked list Lists 7

Algorithm for Inserting at Tail of List new (T); //Create a new Node T. data = A; // store element data T. next = Null; //new node points to Null object If (Head = Null) then Head = T // we have a single else Tail. next = T; node-list Tail= T; // Update Tail to point to the new node © 2004 Goodrich, Tamassia Linked Lists 8

Removing at the Head 1. Update head to point to next node in the list 2. Allow garbage collector to reclaim the former first node 3. Decrement size of list © 2004 Goodrich, Tamassia Linked Lists 9

Algorithm for Removing at the Head If (Head = Null) then Output “error” //empty list else { T = Head; // temporary pointer y = T. data; //save elem data Head = T. next; //update Head If (Head = Null) then Tail = Null; //test for single node Delete(T); //Garbage collection } //End of Algorithm Notice That: Any Removal Algorithm consists of a single statement. © 2004 Goodrich, Tamassia Linked Lists 10

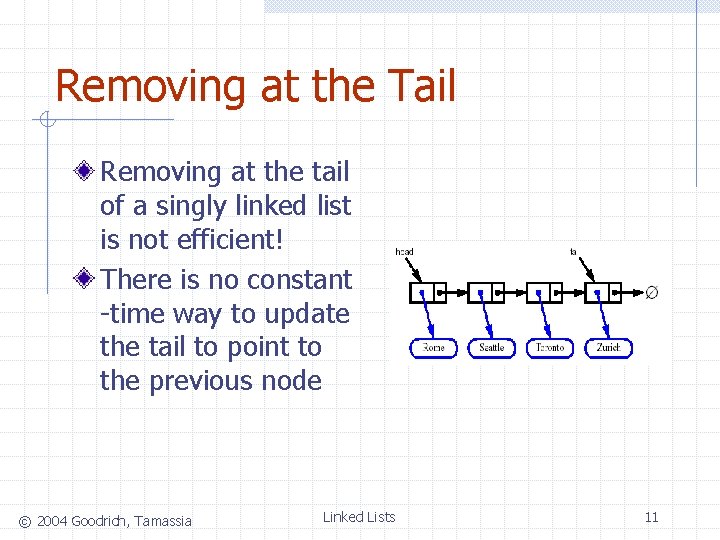
Removing at the Tail Removing at the tail of a singly linked list is not efficient! There is no constant -time way to update the tail to point to the previous node © 2004 Goodrich, Tamassia Linked Lists 11

Algorithm for Removing at the Tail We must cycle through the list (link hopping), starting at the Head, to determine the new Tail-node. If (Head = Null) then Output “error” //empty list else { T = Head; // temporary pointer If (Head=Tail) then {Head=Null; T=Null} // test for single node else { while T. next≠Tail do T=T. next; T. next = Null} y = Tail. data; //save elem data Delete(Tail); //Garbage collection Tail = T; //update Tail } //End of Algorithm © 2004 Goodrich, Tamassia Linked Lists 12

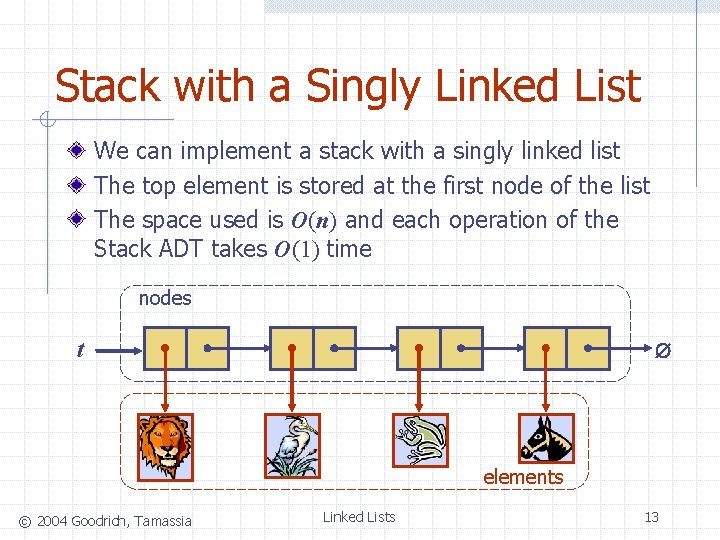
Stack with a Singly Linked List We can implement a stack with a singly linked list The top element is stored at the first node of the list The space used is O(n) and each operation of the Stack ADT takes O(1) time nodes t elements © 2004 Goodrich, Tamassia Linked Lists 13

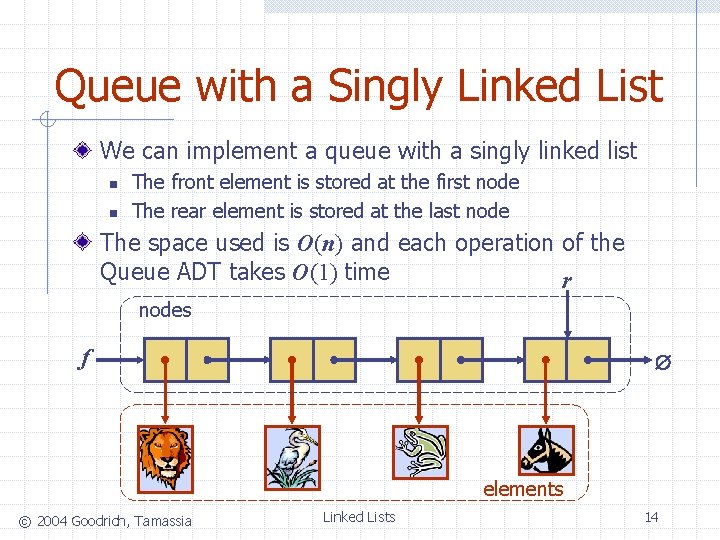
Queue with a Singly Linked List We can implement a queue with a singly linked list n n The front element is stored at the first node The rear element is stored at the last node The space used is O(n) and each operation of the Queue ADT takes O(1) time r nodes f elements © 2004 Goodrich, Tamassia Linked Lists 14