Linked List Ranking Parallel Algorithms 1 Work Analysis

Linked List Ranking Parallel Algorithms 1

Work Analysis – Pointer Jumping l. Number of Steps: Tp = O(Log N) l. Number of Processors: N l. Work = O(N log N) l. T 1 = O(N) l. Work Optimal? ? 2

Common List Ranking Strategy l. Reduce Rank Expand Strategy l. Similar to Odd-Even Prefix Sums l. Algorithms vary in how items are selected for deletion in the Reduce Step l. Some variation in the Expand Step. 3

Reduce Rank Expand l Reduction Step - Delete non-adjacent elements in parallel until the list is of size O(p) (algorithms vary is this step) l Rank Step – Pointer jumping to rank the p remaining elements l Expand Step – Reinsert elements (in the reverse order), computing the rank as it is inserted 4

Asynchronous PRAM – APRAM l Variant of the PRAM model l Features of CRCW PRAM – Plus ¡Processors may have different clock speeds and work asynchronously ¡Each processor has own random number generator 5

Randomized Algorithm l Some portion of the algorithm’s outcome is non-deterministic l Performance stated in terms of expected order of time complexity – EO(f(n)) l EO(f(n)) – with high probability the results are within order f(n) 6

APRAM List Ranking by Martel & Subramonian 1. Select m=EO(n/log n) elements at random 1. Each generates a random number between 1 -N, selects those with values 1 to N / log N 2. Perform log n iterations of pointer jumping 1. Each points to selected, nil, or pointer length log n 3. 4. 5. 6. Pack selected elements to smaller array Scan: each selected points to next selected or nil Compute ranks of selected list-pointer jumping Copy back to original list; scan to complete ranks *EO(n log n) using p = O(n/log n) 7

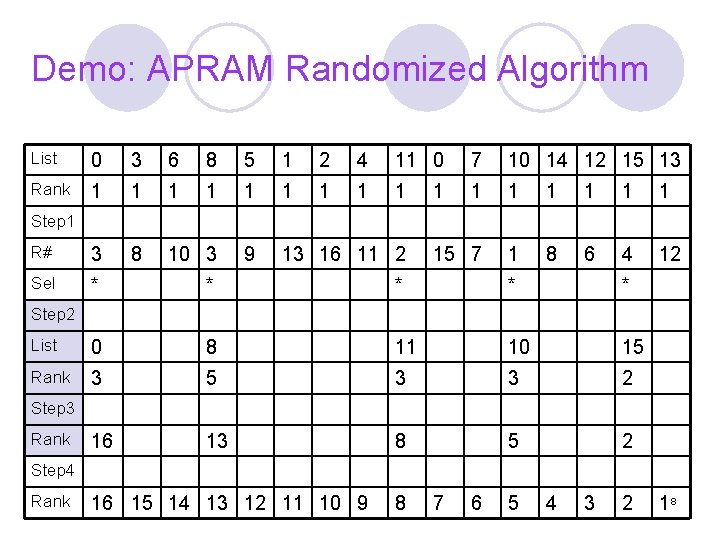
Demo: APRAM Randomized Algorithm List 0 3 6 8 5 1 2 4 11 0 7 10 14 12 15 13 Rank 1 1 1 1 R# 3 8 10 3 9 13 16 11 2 15 7 1 8 6 4 12 Sel * * * List 0 8 11 10 15 Rank 3 5 3 3 2 16 13 8 5 2 1 Step 2 Step 3 Rank Step 4 Rank 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 18

Modifications for EREW Model APRAM l Each PU operates asynchronously EREW l Default execution is synchronous ¡Must synchronize each l Partition the array to at step eliminate Concurrent l Steps 2, 4, 6 allow for Reads Concurrent Reads 9

Randomized EREW Algorithm (4. 1) l Select O(p) elements at random ¡Each generates a random number between 1 -N, selects those with values 1 to N / log N l Pack selected items into smaller array l Scan from selected item to next to set rank l Rank selected elements by pointer jumping l Write ranks back to original array l Scan from selected items to set remaining ranks 10

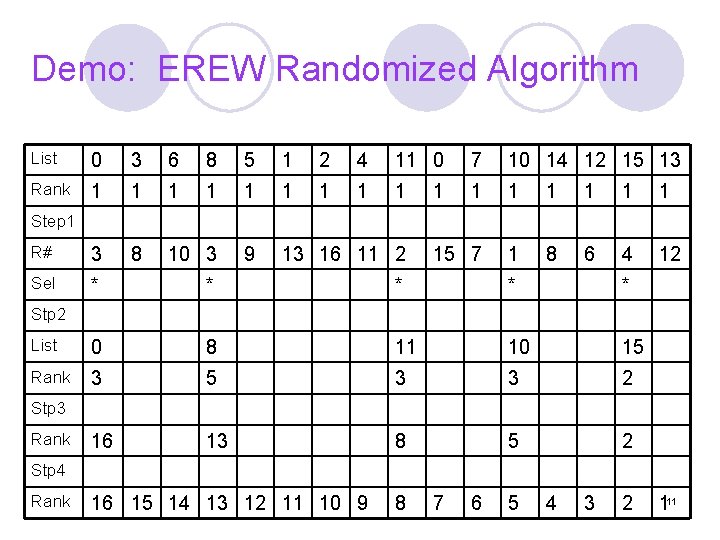
Demo: EREW Randomized Algorithm List 0 3 6 8 5 1 2 4 11 0 7 10 14 12 15 13 Rank 1 1 1 1 R# 3 8 10 3 9 13 16 11 2 15 7 1 8 6 4 12 Sel * * * List 0 8 11 10 15 Rank 3 5 3 3 2 16 13 8 5 2 1 Step 1 Stp 2 Stp 3 Rank Stp 4 Rank 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 111

Complexity Analysis l Selection - EO(n/p) l Compaction - prefix sums EO(n/p + log p) l Form LL - EO(n/p) l Pointer Jumping - EO ( n/p + log p) l Sequential Scan - EO(n/p) l OVERALL - EO ( n/p + log p) l Optimal speedup for p <= O (n / log n) l Which gives EO ( log n) time l See paper for proof. 12

What next? ? l. Can we accomplish an O(log n) deterministic algorithm? l. What was randomized in other algorithms? ¡Can it be made deterministic? 13

Answer! l Yes & No, ¡Can Reduce deterministically! ¡Near Optimal l 2 -Ruling Set (Cole & Vishkin) ¡A subset of the list such that no 2 elements are adjacent & there are exactly 1 or 2 non-ruling set elements between each ruling set element & its nearest successor 14

Deterministic EREW LLR Step 1 l Select a Ruling Set of O(p) elements, O(n/p) distance apart l Keep track of actual distance (for ranking) ¡Repeatedly apply 2 -Ruling Set Algorithm to increase the distance between the elements l Remaining steps are same 15

Complexity Analysis 1. Select O(p) elements O(n/p) distance apart – O(n/p * log (n/p)) 2. Compact – O(n/p + log p) 3. Rank – O(n/p + log p) 4. Write back then Scan – O(n/p) O((log p) + (n/p) * log(n/p)) = O(n/p * log (n/p) ) for n>= p log p = O(log n) for p =O(n/log n) Work O(n log n) 16

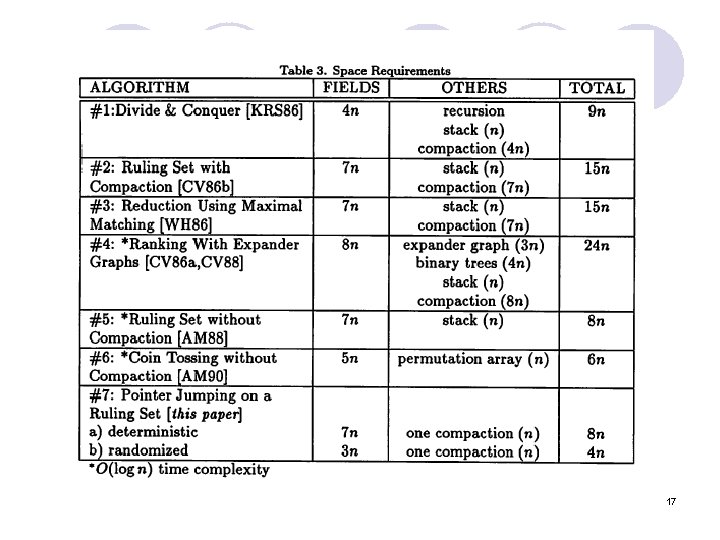
17

Advantages of New Algorithms l. Simple, use basic strategies l. Small constants l. Small space requirements l. Optimal & Near Optimal 18