Link Analysis Page Rank Ranking Nodes on the

Link Analysis: Page. Rank

Ranking Nodes on the Graph • Web pages are not equally “important” www. joe-schmoe. com vs. www. stanford. edu • Since there is large diversity in the connectivity of the web graph we can rank the pages by the link structure Slides by Jure Leskovec: Mining Massive Datasets vs. 2

Link Analysis Algorithms • We will cover the following Link Analysis approaches to computing importances of nodes in a graph: – Page Rank – Hubs and Authorities (HITS) – Topic-Specific (Personalized) Page Rank – Web Spam Detection Algorithms Slides by Jure Leskovec: Mining Massive Datasets 3

Links as Votes • Idea: Links as votes – Page is more important if it has more links • In-coming links? Out-going links? • Think of in-links as votes: – www. stanford. edu has 23, 400 inlinks – www. joe-schmoe. com has 1 inlink • Are all in-links are equal? – Links from important pages count more – Recursive question! Slides by Jure Leskovec: Mining Massive Datasets 4

Simple Recursive Formulation • Each link’s vote is proportional to the importance of its source page • If page p with importance x has n out-links, each link gets x/n votes • Page p’s own importance is the sum of the votes on its in-links p Slides by Jure Leskovec: Mining Massive Datasets 5

Page. Rank: The “Flow” Model • A “vote” from an important page is worth more • A page is important if it is pointed to by other important pages • Define a “rank” rj for node j The web in 1839 y/2 y a/2 a y/2 m m a/2 Flow equations: ry = ry /2 + ra /2 ra = ry /2 + rm rm = ra /2 Slides by Jure Leskovec: Mining Massive Datasets 6

Solving the Flow Equations Flow equations: • 3 equations, 3 unknowns, no constants – No unique solution ry = ry /2 + ra /2 ra = ry /2 + rm rm = ra /2 • Additional constraint forces uniqueness – ry + r a + r m = 1 – ry = 2/5, ra = 2/5, rm = 1/5 • Gaussian elimination method works for small examples, but we need a better method for large web-size graphs Slides by Jure Leskovec: Mining Massive Datasets 7

Page. Rank: Matrix Formulation • Stochastic adjacency matrix M – Let page j has dj out-links – If j → i, then Mij = 1/dj else Mij = 0 • M is a column stochastic matrix – Columns sum to 1 • Rank vector r: vector with an entry per page – ri is the importance score of page i – i ri = 1 • The flow equations can be written r=Mr Slides by Jure Leskovec: Mining Massive Datasets 8

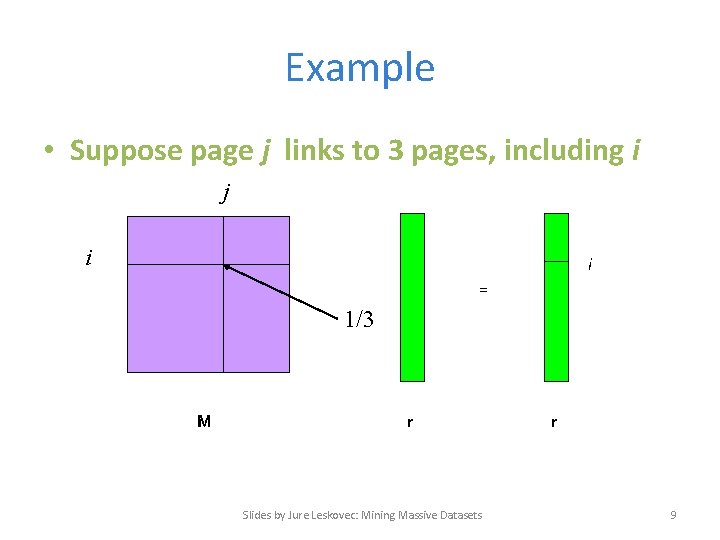
Example • Suppose page j links to 3 pages, including i j i i = 1/3 M r Slides by Jure Leskovec: Mining Massive Datasets r 9

Eigenvector Formulation • The flow equations can be written r=M∙r • So the rank vector is an eigenvector of the stochastic web matrix – In fact, its first or principal eigenvector, with corresponding eigenvalue 1 Slides by Jure Leskovec: Mining Massive Datasets 10

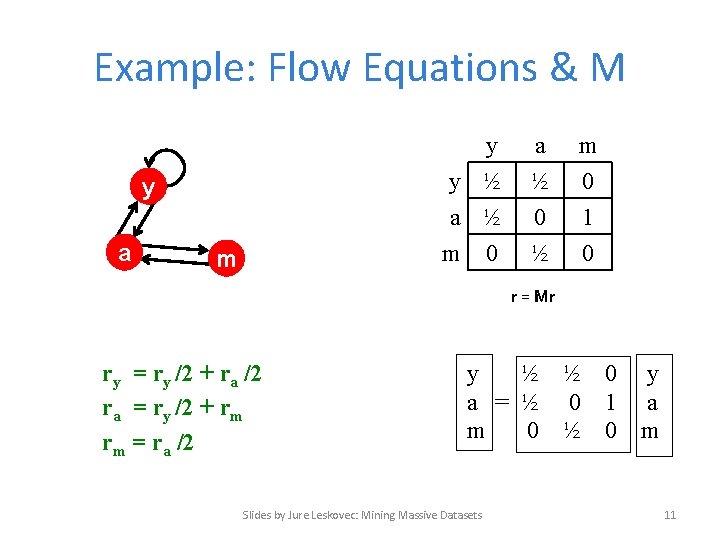
Example: Flow Equations & M y y ½ a ½ m 0 y a m a ½ 0 ½ m 0 1 0 r = Mr ry = ry /2 + ra /2 ra = ry /2 + rm rm = ra /2 y ½ ½ 0 a = ½ 0 1 m 0 ½ 0 Slides by Jure Leskovec: Mining Massive Datasets y a m 11

Power Iteration Method • Given a web graph with n nodes, where the nodes are pages and edges are hyperlinks • Power iteration: a simple iterative scheme – Suppose there are N web pages – Initialize: r(0) = [1/N, …. , 1/N]T – Iterate: r(t+1) = M ∙ r(t) – Stop when |r(t+1) – r(t)|1 < di …. out-degree of node i • |x|1 = 1≤i≤N|xi| is the L 1 norm • Can use any other vector norm e. g. , Euclidean Slides by Jure Leskovec: Mining Massive Datasets 12

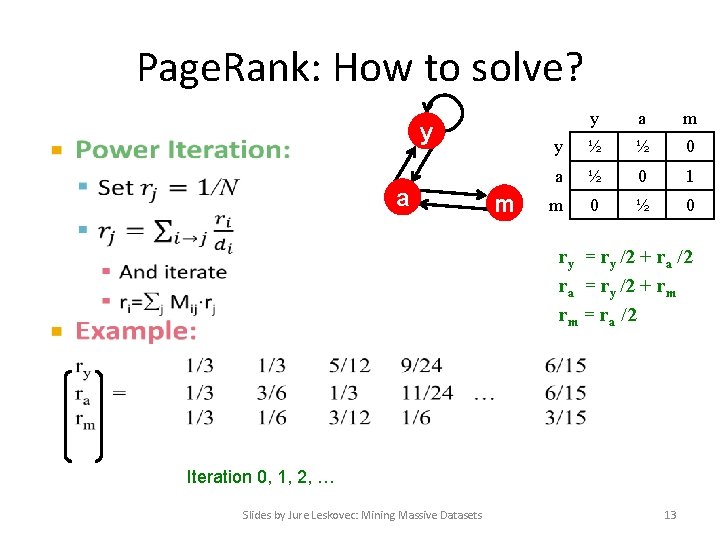
Page. Rank: How to solve? y • a m y ½ ½ 0 a ½ 0 1 m 0 ½ 0 ry = ry /2 + ra /2 ra = ry /2 + rm rm = ra /2 Iteration 0, 1, 2, … Slides by Jure Leskovec: Mining Massive Datasets 13

Random Walk Interpretation �Imagine a random web surfer: i 1 – At any time t, surfer is on some page u – At time t+1, the surfer follows an out-link from u uniformly at random – Ends up on some page v linked from u – Process repeats indefinitely i 2 i 3 j �Let: �p(t) … vector whose ith coordinate is the prob. that the surfer is at page i at time t – p(t) is a probability distribution over pages Slides by Jure Leskovec: Mining Massive Datasets 14

The Stationary Distribution • Where is the surfer at time t+1? i 1 – Follows a link uniformly at random i 2 i 3 j p(t+1) = M · p(t) • Suppose the random walk reaches a state p(t+1) = M · p(t) = p(t) then p(t) is stationary distribution of a random walk �Our rank vector r satisfies r = M · r – So, it is a stationary distribution for the random walk Slides by Jure Leskovec: Mining Massive Datasets 15

Page. Rank: Three Questions or equivalently • Does this converge? • Does it converge to what we want? • Are results reasonable? Slides by Jure Leskovec: Mining Massive Datasets 16

Does This Converge? a • Example: = ra rb b 1 0 0 1 Iteration 0, 1, 2, … 1 0 0 1 Slides by Jure Leskovec: Mining Massive Datasets 17

Does it Converge to What We Want? a • Example: ra = rb b 1 0 0 0 0 Iteration 0, 1, 2, … Slides by Jure Leskovec: Mining Massive Datasets 18

Problems with the “Flow” Model 2 problems: • Some pages are “dead ends” (have no out-links) – Such pages cause importance to “leak out” • Spider traps (all out links are within the group) – Eventually spider traps absorb all importance Slides by Jure Leskovec: Mining Massive Datasets 19

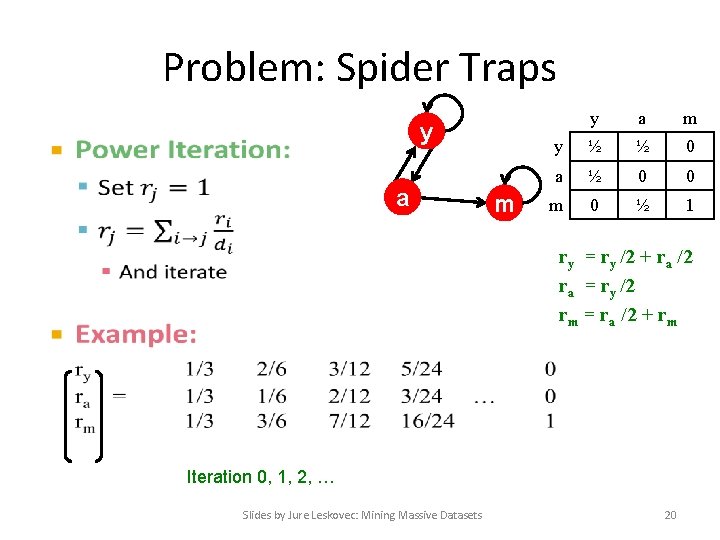
Problem: Spider Traps y • a m y ½ ½ 0 a ½ 0 0 m 0 ½ 1 ry = ry /2 + ra /2 ra = ry /2 rm = ra /2 + rm Iteration 0, 1, 2, … Slides by Jure Leskovec: Mining Massive Datasets 20

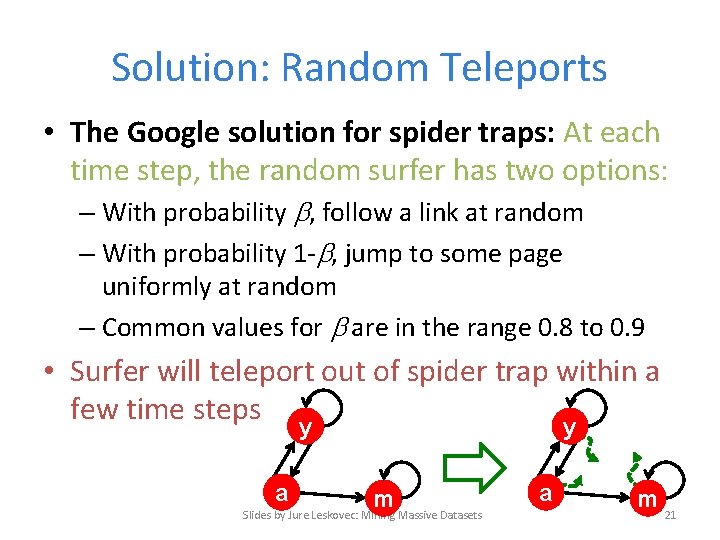
Solution: Random Teleports • The Google solution for spider traps: At each time step, the random surfer has two options: – With probability , follow a link at random – With probability 1 - , jump to some page uniformly at random – Common values for are in the range 0. 8 to 0. 9 • Surfer will teleport out of spider trap within a few time steps y y a m Slides by Jure Leskovec: Mining Massive Datasets a m 21

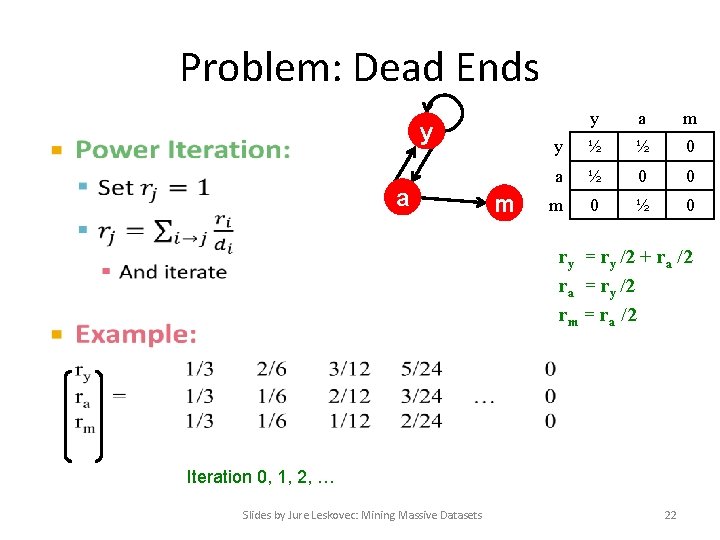
Problem: Dead Ends y • a m y ½ ½ 0 a ½ 0 0 m 0 ½ 0 ry = ry /2 + ra /2 ra = ry /2 rm = ra /2 Iteration 0, 1, 2, … Slides by Jure Leskovec: Mining Massive Datasets 22

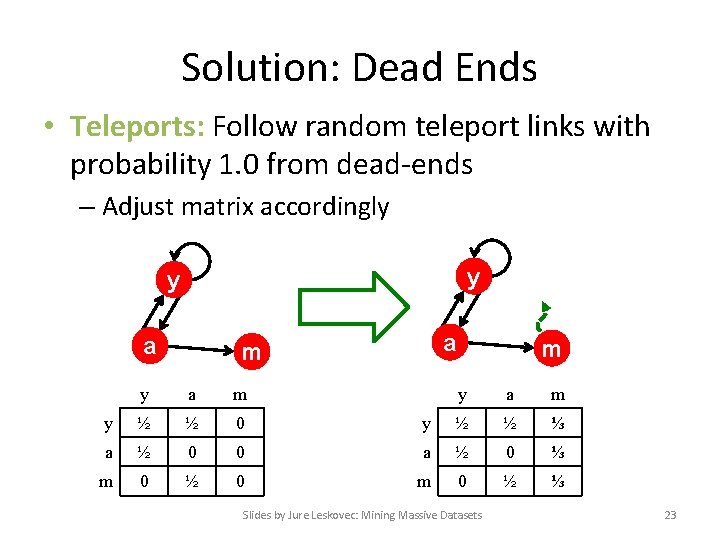
Solution: Dead Ends • Teleports: Follow random teleport links with probability 1. 0 from dead-ends – Adjust matrix accordingly y y a a m y ½ ½ 0 a ½ 0 m 0 ½ m y a m y ½ ½ ⅓ 0 a ½ 0 ⅓ 0 m 0 ½ ⅓ Slides by Jure Leskovec: Mining Massive Datasets 23

Why Teleports Solve the Problem? Markov Chains • Set of states X • Transition matrix P where Pij = P(Xt=i | Xt-1=j) • π specifying the probability of being at each state x X • Goal is to find π such that π = P π Slides by Jure Leskovec: Mining Massive Datasets 24

Why is This Analogy Useful? • Theory of Markov chains • Fact: For any start vector, the power method applied to a Markov transition matrix P will converge to a unique positive stationary vector as long as P is stochastic, irreducible and aperiodic. Slides by Jure Leskovec: Mining Massive Datasets 25

Make M Stochastic • Stochastic: Every column sums to 1 • A possible solution: Add green links • • y a m y ½ ½ 1/3 a ½ 0 1/3 m 0 ½ 1/3 ai…=1 if node i has out deg 0, =0 else 1…vector of all 1 s ry = ry /2 + ra /2 + rm /3 ra = ry /2+ rm /3 rm = ra /2 + rm /3 Slides by Jure Leskovec: Mining Massive Datasets 26

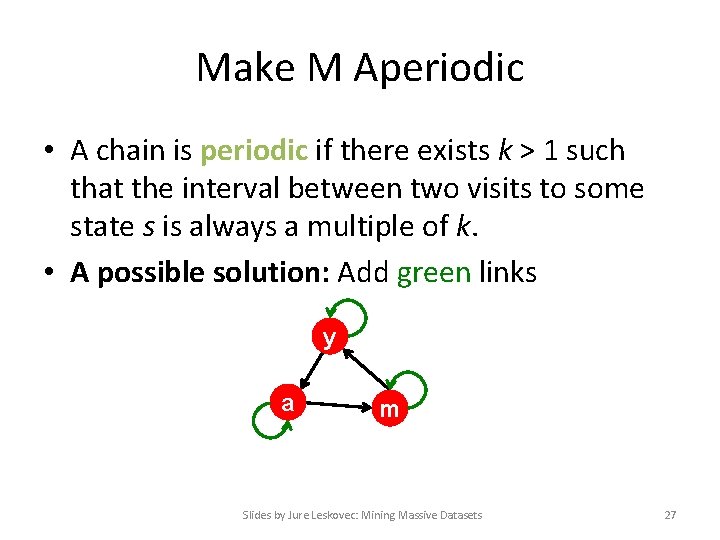
Make M Aperiodic • A chain is periodic if there exists k > 1 such that the interval between two visits to some state s is always a multiple of k. • A possible solution: Add green links y a m Slides by Jure Leskovec: Mining Massive Datasets 27

Make M Irreducible • From any state, there is a non-zero probability of going from any one state to any another • A possible solution: Add green links y a m Slides by Jure Leskovec: Mining Massive Datasets 28

Solution: Random Jumps • From now on: We assume M has no dead ends That is, we follow random teleport links by Jure Leskovec: Mining Massive Datasets with. Slides probability 1. 0 from dead-ends di … out-degree of 29 node i

The Google Matrix • Slides by Jure Leskovec: Mining Massive Datasets 30

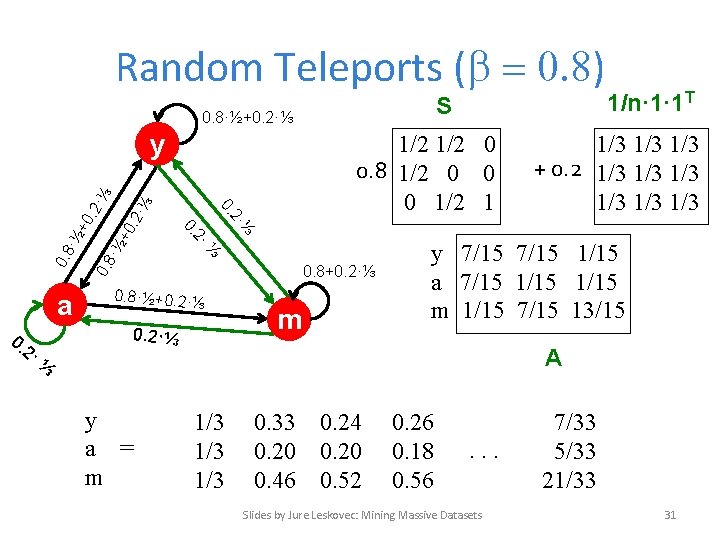
Random Teleports ( = 0. 8) S 0. 8·½+0. 2·⅓ ·⅓ +0. 2 ·½ 0. 8 ⅓ 0. 8+0. 2·⅓ 0. 8·½+0. 2·⅓ m y 7/15 1/15 a 7/15 1/15 m 1/15 7/15 13/15 A ⅓ y a = m 1/3 1/3 + 0. 2 1/3 1/3 1/3 2· 0. 2· 1/2 0 0. 8 1/2 0 0 0 1/2 1 ⅓ 0. 2· a 0. +0. 2 ·⅓ y 1/n· 1· 1 T 1/3 1/3 0. 33 0. 24 0. 20 0. 46 0. 52 0. 26 0. 18 0. 56 . . . Slides by Jure Leskovec: Mining Massive Datasets 7/33 5/33 21/33 31

Computing Page Rank • Key step is matrix-vector multiplication – rnew = A ∙ rold • Easy if we have enough main memory to hold A, rold, rnew • Say N = 1 billion pages A = ∙M + (1 - ) [1/N] – We need 4 bytes for each entry (say) – 2 billion entries for vectors, approx 8 GB – Matrix A has N 2 entries A = 0. 8 • 1018 is a large number! Slides by Jure Leskovec: Mining Massive Datasets ½ ½ 0 0 0 ½ 1 +0. 2 Nx. N 1/3 1/3 1/3 7/15 1/15 = 7/15 1/15 7/15 13/15 32

Matrix Formulation • Suppose there are N pages • Consider a page j, with set of out-links dj • We have Mij = 1/|dj| when j→i and Mij = 0 otherwise • The random teleport is equivalent to – Adding a teleport link from j to every other page with probability (1 - )/N – Reducing the probability of following each out-link from 1/|dj| to /|dj| – Equivalent: Tax each page a fraction (1 - ) of its score and redistribute evenly Slides by Jure Leskovec: Mining Massive Datasets 33

Rearranging the Equation • [x]N … a vector of Slides by Jure Leskovec: Mining Massive Datasets length N with all entries x 34

Sparse Matrix Formulation • Slides by Jure Leskovec: Mining Massive Datasets 35

Sparse Matrix Encoding • Encode sparse matrix using only nonzero entries – Space proportional roughly to number of links – Say 10 N, or 4*10*1 billion = 40 GB – Still won’t fit in memory, but will fit on disk source degree node destination nodes 0 3 1, 5, 7 1 5 17, 64, 113, 117, 245 2 2 13, 23 Slides by Jure Leskovec: Mining Massive Datasets 36

Basic Algorithm: Update Step • Assume enough RAM to fit rnew into memory – Store rold and matrix M on disk • Then 1 step of power-iteration is: Initialize all entries of rnew to (1 - )/N For each page p (of out-degree n): Read into memory: p, n, dest 1, …, destn, rold(p) for j = 1…n: rnew(destj) += rold(p) / n rold rnew 0 1 2 3 4 5 6 src 0 1 2 degree 3 4 2 destination 1, 5, 6 17, 64, 113, 117 13, 23 Slides by Jure Leskovec: Mining Massive Datasets 0 1 2 3 4 5 6 37

Analysis • Assume enough RAM to fit rnew into memory – Store rold and matrix M on disk • In each iteration, we have to: – Read rold and M – Write rnew back to disk – IO cost = 2|r| + |M| • Question: – What if we could not even fit rnew in memory? Slides by Jure Leskovec: Mining Massive Datasets 38

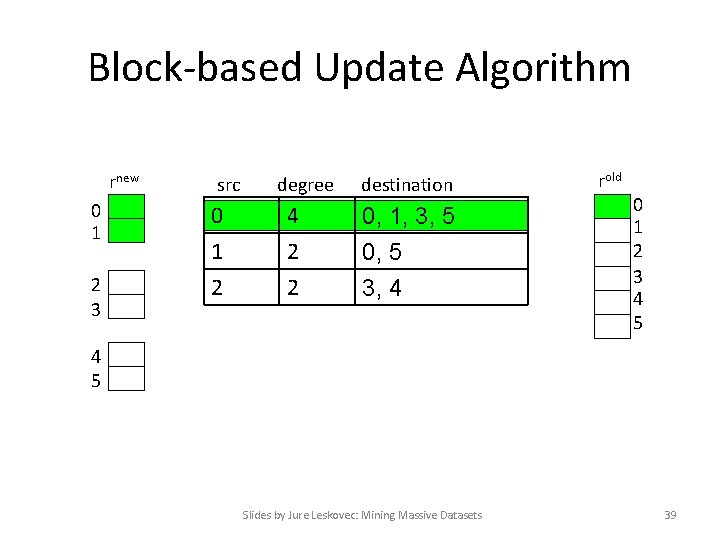
Block-based Update Algorithm rnew 0 1 2 3 src 0 1 2 degree 4 2 2 destination 0, 1, 3, 5 0, 5 3, 4 rold 0 1 2 3 4 5 Slides by Jure Leskovec: Mining Massive Datasets 39

Analysis of Block Update • Similar to nested-loop join in databases – Break rnew into k blocks that fit in memory – Scan M and rold once for each block • k scans of M and rold – k(|M| + |r|) + |r| = k|M| + (k+1)|r| • Can we do better? – Hint: M is much bigger than r (approx 10 -20 x), so we must avoid reading it k times per iteration Slides by Jure Leskovec: Mining Massive Datasets 40

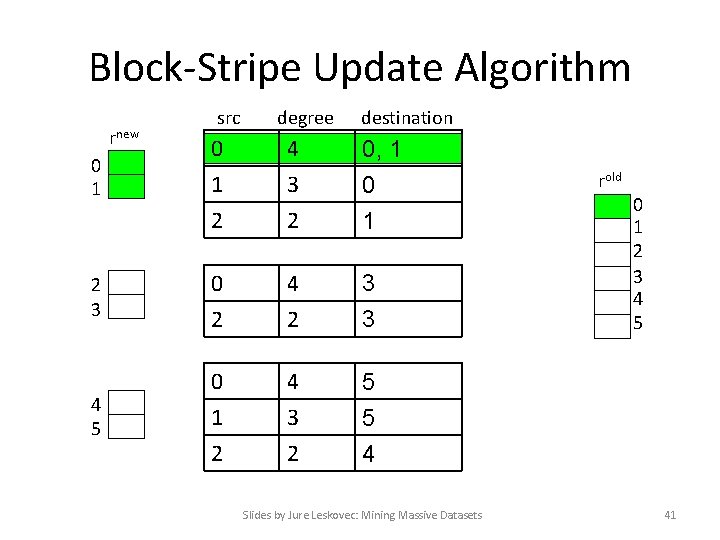
Block-Stripe Update Algorithm rnew src degree destination 0 1 2 4 3 2 0, 1 0 1 2 3 0 2 4 2 3 3 4 5 0 1 2 4 3 2 5 5 4 Slides by Jure Leskovec: Mining Massive Datasets rold 0 1 2 3 4 5 41

Block-Stripe Analysis • Break M into stripes – Each stripe contains only destination nodes in the corresponding block of rnew • Some additional overhead per stripe – But it is usually worth it • Cost per iteration – |M|(1+ ) + (k+1)|r| Slides by Jure Leskovec: Mining Massive Datasets 42

Some Problems with Page Rank • Measures generic popularity of a page – Biased against topic-specific authorities – Solution: Topic-Specific Page. Rank (next) • Uses a single measure of importance – Other models e. g. , hubs-and-authorities – Solution: Hubs-and-Authorities (next) • Susceptible to Link spam – Artificial link topographies created in order to boost page rank – Solution: Trust. Rank (next) Slides by Jure Leskovec: Mining Massive Datasets 43