Linier Programming Metode Grafik Dian Rachmawati Pendahuluan Linear

Linier Programming Metode Grafik Dian Rachmawati

Pendahuluan Linear Programming dengan metode grafik untuk fungsi tujuan baik maksimum maupun minimum. Pada Metode Grafik variabel keputusan yang akan muncul adalah 2 variabel. Harapan setelah mempelajari Linear Programming metode grafik adalah : 1. Mengenal linear programming sebagai alat pengambilan keputusan 2. Merumuskan permasalahan operasi ke dalam bentuk linear programming 3. Menyelesaikan permasalahan linear programming dengan grafik/ matematik

Metode Grafik FORMULASI PERMASALAHAN, langkah-langkah : 1. Analisis secara menyeluruh permasalahan manajerial yang dihadapi 2. Definisikan variabel keputusannya 3. Identifikasikan tujuan dan kendalanya 4. Gunakan variabel keputusan untuk merumuskan fungsi tujuan dan fungsi kendala secara matematis.

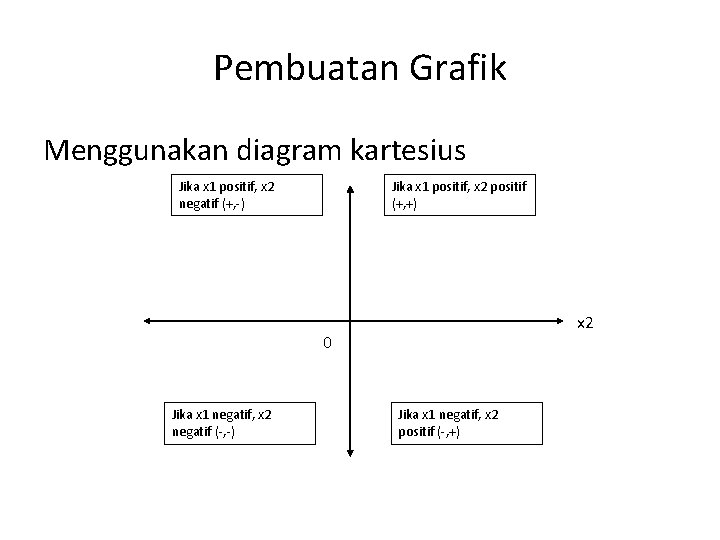
Pembuatan Grafik Menggunakan diagram kartesius Jika x 1 positif, x 2 negatif (+, -) Jika x 1 positif, x 2 positif (+, +) x 2 0 Jika x 1 negatif, x 2 negatif (-, -) Jika x 1 negatif, x 2 positif (-, +)

Tipe solusi dalam pemrograman Linear • Solusi Layak (feasible solution) adalah solusi dimana semua kendala yang ada terpenuhi • Solusi tak layak (infeasible solution) adalah solusi di mana sedikitnya satu kendala tidak terpenuhi atau dengan kata lain dilanggar

Istilah lain : • Daerah Layak adalah kumpulan semua solusi layak • Solusi Optimal adalah solusi layak yang memiliki nilai fungsi tujuan terbaik. Nilai yang paling baik adalah nilai terbesar jika fungsi tujuannya adalah memaksimalkan, begitu juga sebaliknya, yaitu nilai terkecil jika tujuannya minimal.

Contoh Permasalahan PT Krisna Furniture yang akan membuat meja dan kursi. Keuntungan yang diperoleh dari satu unit meja adalah $7, - sedang keuntungan yang diperoleh dari satu unit kursi adalah $5, -. Namun untuk meraih keuntungan tersebut Krisna Furniture menghadapi kendala keterbatasan jam kerja. Untuk pembuatan 1 unit meja dia memerlukan 4 jam kerja. Untuk pembuatan 1 unit kursi dia membutuhkan 2 jam kerja. Untuk pengecatan 1 unit meja dibutuhkan 2 jam kerja, dan untuk pengecatan 1 unit kursi dibutuhkan 1 jam kerja. Jumlah jam kerja yang tersedia untuk pembuatan meja dan kursi adalah 240 jam per minggu Jumlah jam kerja untuk pengecatan adalah 100 jam per minggu. Berapa jumlah meja dan kursi yang sebaiknya diproduksi per minggu agar keuntungan perusahaan maksimum?

Penyelesaian Permasalahan Formulasi Permasalahan : 1. Analisis • Tujuan perusahaan adalah memaksimumkan profit • Variabel yg akan dicari berapa banyak meja (x 1) dan kursi (x 2) yang harus dibuat.

Lanjutan 2. Variabel Keputusan Variabel yg akan dicari berapa banyak meja (x 1) dan kursi (x 2) yang harus dibuat

Lanjutan •

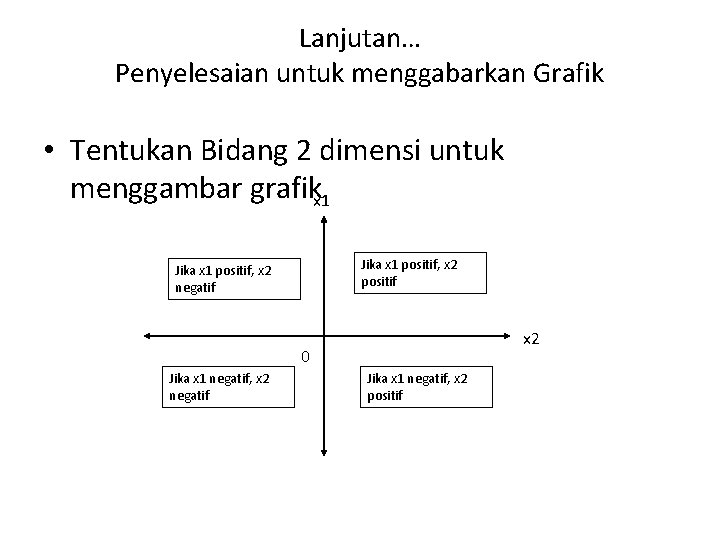
Lanjutan… Penyelesaian untuk menggabarkan Grafik • Tentukan Bidang 2 dimensi untuk menggambar grafikx 1 Jika x 1 positif, x 2 positif Jika x 1 positif, x 2 negatif x 2 0 Jika x 1 negatif, x 2 negatif Jika x 1 negatif, x 2 positif

Ubah tanda Batasan /kendala dg = •

Cari titik potong dengan sumbu x 1 dan x 2 1. Kendala 1. 2 x 1 + x 2 = 120 Titik potong dg sumbu x 1, nilai x 1 = 0 Masukkan nilai 0 pada x 1, hasilnya : 2 x 0 + x 2 = 120 Hasil (x 2, x 1) : (120, 0) Titik Potong dg sumbu x 2, nilai x 2 = 0 Masukkan nilai 0 pada x 2, hasilnya : 2 x 1 + 0 = 120 2 x 1 = 120/2 x 1 = 60 Hasil (x 2, x 1) : ( 0, 60) x 1 x 2 0 x 1 120 x 2 60 0

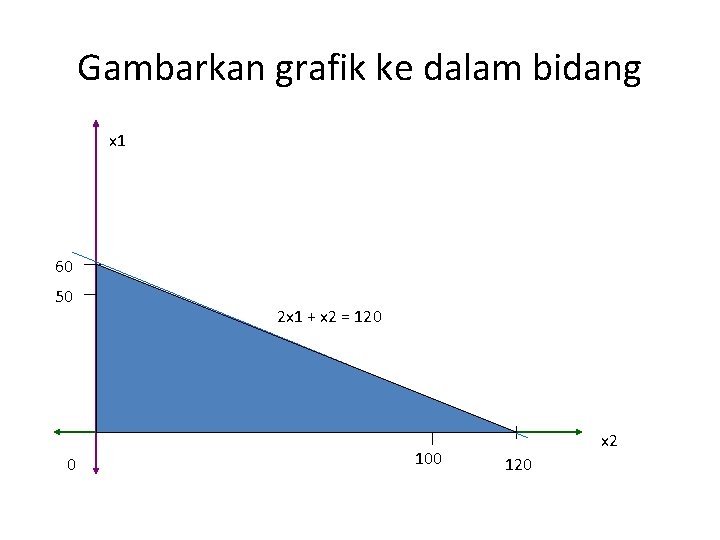
Gambarkan grafik ke dalam bidang x 1 60 50 0 2 x 1 + x 2 = 120 100 x 2 120

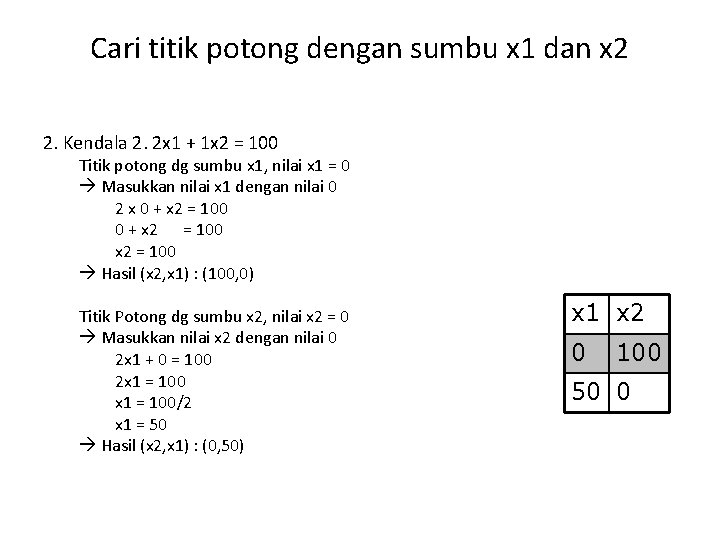
Cari titik potong dengan sumbu x 1 dan x 2 2. Kendala 2. 2 x 1 + 1 x 2 = 100 Titik potong dg sumbu x 1, nilai x 1 = 0 Masukkan nilai x 1 dengan nilai 0 2 x 0 + x 2 = 100 Hasil (x 2, x 1) : (100, 0) Titik Potong dg sumbu x 2, nilai x 2 = 0 Masukkan nilai x 2 dengan nilai 0 2 x 1 + 0 = 100 2 x 1 = 100/2 x 1 = 50 Hasil (x 2, x 1) : (0, 50) x 1 x 2 0 100 50 0

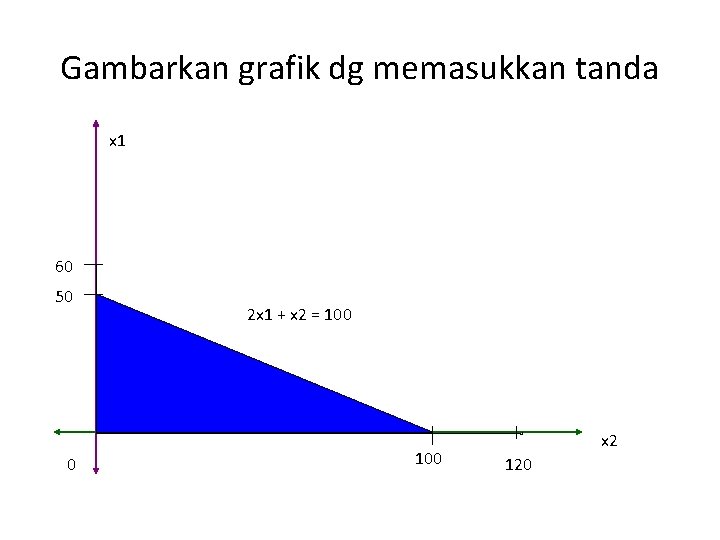
Gambarkan grafik dg memasukkan tanda x 1 60 50 2 x 1 + x 2 = 100 2 x 1 + 1 x 2 = 100 0 100 x 2 120

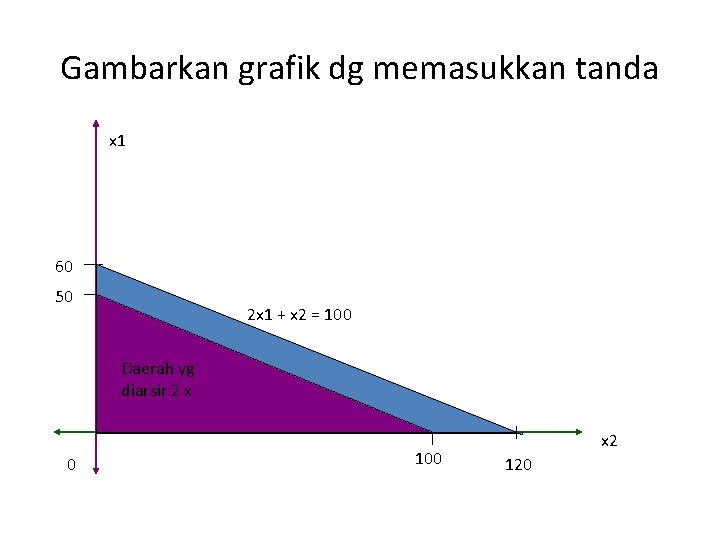
Gambarkan grafik dg memasukkan tanda x 1 60 50 2 x 1 + x 2 = 100 Daerah yg 2 x 1 +21 x 2 diarsir x = 100 0 100 x 2 120

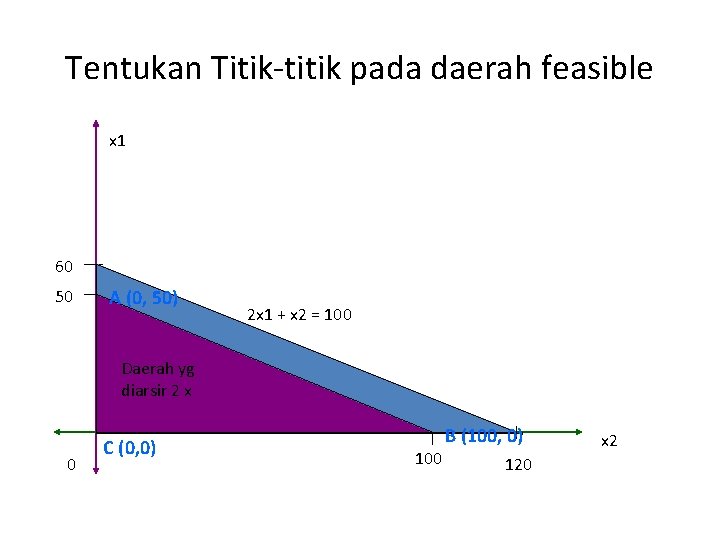
Tentukan Titik-titik pada daerah feasible x 1 60 50 A (0, 50) 2 x 1 + x 2 = 100 Daerah yg 2 x 1 +21 x 2 diarsir x = 100 0 C (0, 0) 100 B (100, 0) 120 x 2

Pencarian nilai Z mak = 7 x 1 + 5 x 2 Masukkan nilai-nilai yang mungkin : 1. Titik A (0, 50) 2. Titik B (100, 0) 3. Titik C (0, 0)

Titik A (0, 50) Z mak = 7 x 1 + 5 x 2 Z mak = (7 x 0) + (5 x 50) Z mak = 0 + 250 Z mak = 250

Titik B (100, 0) Z mak = 7 x 1 + 5 x 2 Z mak = (7 x 100) + (5 x 0) Z mak = 700 + 0 Z mak = 700

Titik C (0, 0) Z mak = 7 x 1 + 5 x 2 Z mak = (7 x 0) + (5 x 0) Z mak = 0 + 0 Z mak = 0

Pilih yang paling MAKSIMAL 1. Titik A (0, 50) = 250 2. Titik B (100, 0) = 700 3. Titik C (0, 0) = 0 MAKSIMAL

Contoh • Perusahaan pabrikasi menghasilkan pintu kaca dan jendela kaca. Setiap pintu kaca memerlukan 6 jam dr waktu pekerja didepartemen 1 dan 2 jam dr waktu pekerja di departemen 2. Sementara itu untuk membuat jendela kaca membutuhkan 4 jam pekerjaan di departemen 1 dan 3 jam pekerjaan di departemen 2. Keuntungan untuk setiap pintu kaca dan jendela kaca masing-masing adalah Rp 25000, - dan Rp. 20000, -. Terdapat total waktu 60 jam pekerja di departemen 1 dan total waktu 30 jm pekerja di departemen 2. Tentukan keuntungan maksimum dari kombinasi produk yang ada.

Contoh • Seorang petani memerlukan paling sedikit 30 unit zat A dan 24 unit zat B untuk puuk tanaman di lahannya. kedua zat tersebut dapat di peroleh dari pupuk cair dan pupuk padat. setiap botol pupuk cair harganya 20. 000 mengandung 5 unit zat A dan 3 unit zat B, sedangkan setiap kantung pupuk padat seharga 16. 000 mengandung 3 unit zat A dan 4 unit zat B. Bagaimana cara untuk mencari model matematika untuk meminimumkan biaya petani itu

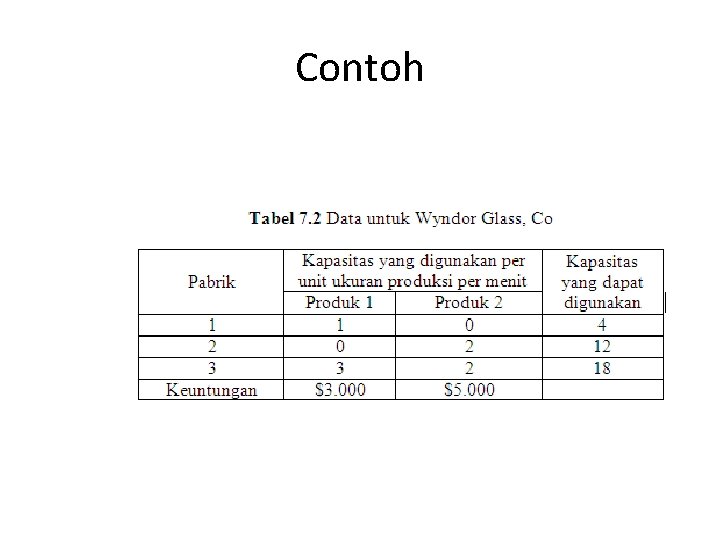
Contoh: Wyndor Glass, Co memproduksi kaca berkualitas tinggi untuk digunakan sebagai jendela dan pintu kaca. Perusahaan ini memiliki tiga buah pabrik (plant) yaitu pabrik 1 yang membuat bingkai aluminium, pabrik 2 membuat bingkai kayu, dan pabrik 3 memproduksi kaca dan merakit produk secara keseluruhan. Perusahaan mendapatkan pesanan berupa dua macam produk baru yang potensial, yaitu pintu kaca setinggi 8 kaki dan bingkai aluminium (produk 1) dan jendela berukuran 4 x 6 kaki dengan bingkai kayu (produk 2).

Contoh Karena perusahaan sedang mengalami penurunan pendapatan akibat resesi ekonomi dunia, maka pihak manajemen produksi harus memikirkan kapasitas produksi sehingga mampu menghasilkan dua produk potensial tersebut dengan keuntungan yang besar. Akan tetapi, di pabrik 3 kedua produk tersebut bersaing untuk menggunakan kapasitas produksi yang ada (lihat tabel 4. 2). Untuk itu, anda diminta untuk membantu manajer produksi untuk menentukan berapa banyakkah masing-masing produk harus dibuat sehingga diperoleh keuntungan optimal?

Contoh