Linguistic Knowledge Representation Scott Farrar Department of Linguistics

Linguistic Knowledge Representation Scott Farrar Department of Linguistics farrar@u. arizona. edu

Problems to Overcome 1. Specifying the relationship between linguistic and other forms of knowledge.

Inference from Knowledge L-Linguistic John’s hand is in his pocket. CS-Commonsense V-Visual L John owns the hand. CS, V The hand is physically attached to John. L, CS The hand is physically contained in the pocket, not the other way around. V A hand is smaller than a pocket. CS John’s hand is not in Bill’s pocket. CS John’s wants his hand to be in his pocket. L This event is occurring now. CS Hand is a body-part, not a person. CS A pocket is a container in clothing.

Problems to Overcome 1. 2. Specifying the relationship between linguistic and other forms of knowledge. Dealing with ambiguity and other issues of natural language processing (NLP).

What is Meaning? n Symbols, Representation, Extensions [010011101] moon

What is Meaning? n Conceptual structure hypothesis: The meaning of a word is the corresponding mental representation in the mind of an agent.

The Lexicon links Linguistic Knowledge to the Rest of Cognition Auditory input Vision input Syntactic Structure Conceptual Structure Spatial Structure Haptic input Motor output Jackendoff’s Model

The Computational Lexicon n form—what data structures comprise the lexicon? organization—how are the data structures organized? content—what information is contained in the data structures?

Form of the Lexicon n Features—Katz and Fodor (1963): knowledge is a conjunction of features (monadic predicates) bachelor (x)→ unmarried (x) & male (x) & young (x)

Form of the Lexicon n Frames—Minsky (1975): knowledge is organized around concepts give: <agent Person> <recipient Person> <theme Physical. Object> slots values

Form of the Lexicon n Attribute-value matrices (feature structures) From knowledge engineering (AI) community e. g. , Head-Driven Phrase Structure Grammar <see example>

Organization of the Lexicon n Semantic network—Quillian (1966): knowledge is interconnected has-part animal Sub lungs has-part bird Inst tweety feathers

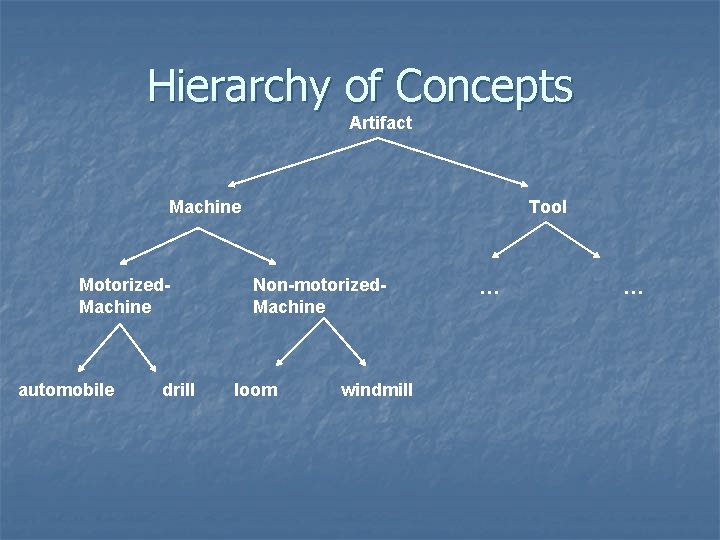
Hierarchy of Concepts Artifact Machine Motorized. Machine automobile drill Tool Non-motorized. Machine loom windmill … …

Problems to Overcome 1. 2. 3. Specifying the relationship between linguistic and other forms of knowledge. Dealing with ambiguity and other issues of natural language processing (NLP). Determining what role visual knowledge of objects and events has in the disambiguation process.

Formalism for Ambiguity Resolution (9/13/02) Scott Farrar Department of Linguistics farrar@u. arizona. edu

Goals of the Present Research n Build a theoretical system that can construct a visual scene from English text input. focus on the problem of lexical ambiguity n access and use the visual knowledge linked to lexical items n argue for a knowledge-rich approach to natural language processing (lexicon) n

Lexical Ambiguity When one linguistic form has multiple meanings: The book is on the edge of the table. The edge of the table is sharp. [area] [line] The park is five blocks away. Kids like to play with blocks. [large dimension] [small dimension] The middle (of the bench) is wet. [center-part] Put the pan in the middle (between the bowls). [space-between] To vote “YES” check the upper box. Put your hand in the box. [2 d] [3 d]

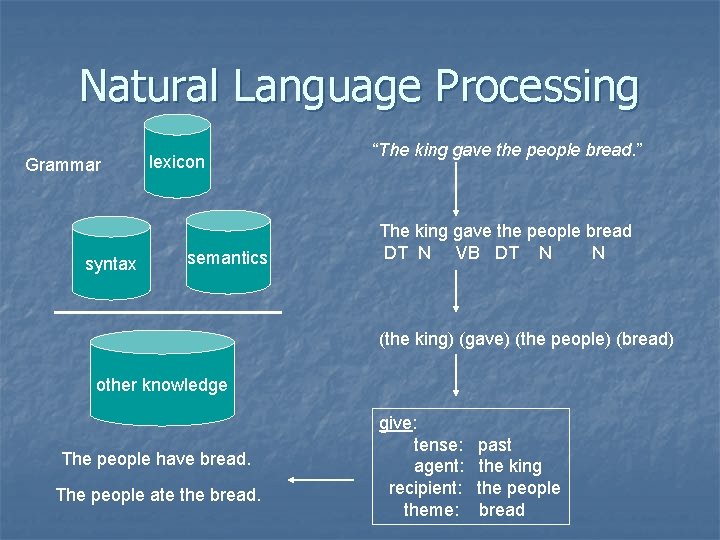
Natural Language Processing Grammar syntax lexicon semantics “The king gave the people bread. ” The king gave the people bread DT N VB DT N N (the king) (gave) (the people) (bread) other knowledge The people have bread. The people ate the bread. give: tense: agent: recipient: theme: past the king the people bread

How much visual knowledge does the lexicon have access to? Type of concept a. a-spatial b. extrinsically spatial c. intrinsically spatial d. strictly spatial (Bierwisch 1996: 52) Example fear, hour, duration animal, robot, instrument horse, man, violin my leg square, margin, height

Content of the Lexicon Purely linguistic: dog “dog”, [da: g] dog collar not *collar dog+PL = dogs not *doges

Content of the Lexicon Purely visual: dog shape: size: color: texture:

Content of the Lexicon Commonsense/other/visual: dog has-part (dog, tail) makes-noise (dog, “bark”) disjoint (dog cat) likes (Scott, terrier)

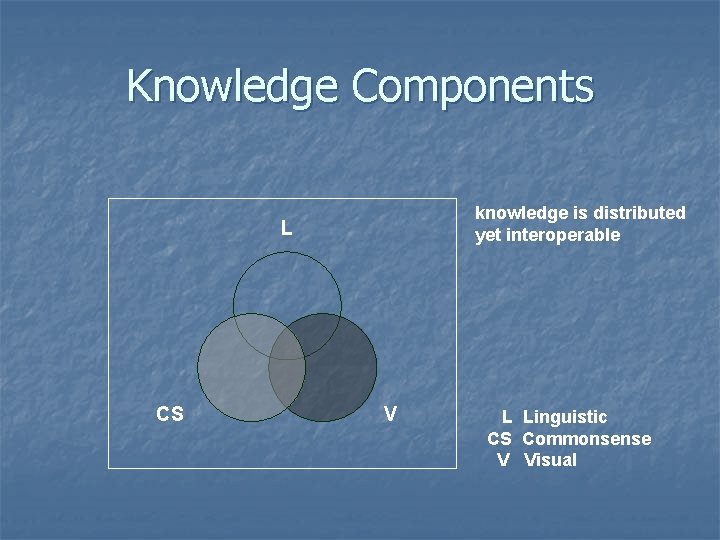
Knowledge Components knowledge is distributed yet interoperable L CS V L Linguistic CS Commonsense V Visual

Formalization of the Problem n input: a list of well-formed English utterances U, where U={u 1, u 2, u 3, …, un}, |U|≥ 1, and U can be interpreted as a complete visual scene.

Examples of U {John is standing on the bridge. John has his hands in his pockets. John is wearing a cap…} {The table is in the middle of the room. There is a ball on the edge of the table…} not {Mary loves John. She has known him for four years…}

Formalization of the Problem (cont. ) n output: VU, such that VU is a visual scene based on U consisting of a 3 -tuple <I, O, R> where I is a set of icons, O is a set of orientations for the icons, and R is a set of relations among the icons.

A Solution Approach n n n Represent all knowledge in pure first-order logic a knowledge base KB consists of axioms and facts about the domain with no distinctions made between types of knowledge a forward-chaining algorithm is used to generate a visual scene

Formalization of the Lexicon A lexicon L is at least the 4 -tuple <F, R, G, C>, where: F is the set of linguistic forms. R is the set of formal relations among members of F. G is the grammatical information relevant to F. C is the conceptual content (the meaning).

Commonsense Knowledge n n n A ball will not remain stationary on an inclined surface. A jar can be a container. Unsupported objects fall.

Formalization of Commonsense Knowledge n KB is the tuple <C, R, I, O>, where: C is the (possibly infinite) set of concepts. R is set of relations over C. I is the set of individuals. O is an ontology specifying the precise formalization of C, R, and I.

Visual Knowledge Concepts: Abstract. Shapes={Circle, Line, Sphere, …} Relations: Spatial. Relations={In, On, Contains, …} Axioms: Peas are smaller than landmines. If object A contacts object B, then A is near B.

Formalization of Visual Knowledge Visual knowledge V is a subset of KB.

So far so Good n lexicon L = <F, R, G, C> knowledge base KB = <C, R, I, O> n visual knowledge V ∈ KB n * Well understood inferencing procedures for FOL knowledge bases: theorem proving: Prolog, forwardchaining: CLIPS

So Far so Intractable * If represented in pure first-order (or higher order) logic, then the problem will eventually become computationally intractable depending on scope of domain and, for NLP, ambiguity of the word in question (compare ‘edge’ to ‘hand’).

Alternatives n Use a logical system that is wellunderstood and known to be complete and tractable Description Logic (Brachman 1979)

Description Logic n n n n A KR formalism (like frames, semantic nets, prod. syst. ) A way to build a conceptualization of the domain Basic structure is the concept (a structured entity) Intuitively appealing Incorporates a subset of FOL Expressive syntax and decidable inference procedures e. g. , KL-ONE (Brachman 1979) KRYPTON (Brachman, Fikes, and Levesque (1983) LOOM, CLASSIC…

Description Logic Components n n n Syntax The KB Semantics Reasoning Procedures Reasoning Tasks

Syntax: Atoms n n n concepts roles individuals (unary predicates) (binary predicates) (constants)

Syntax: Concepts n n n Round Flat Long Hole Person Event

Syntax: Roles n n n On In Strike Touch Neighbor Father

Syntax: Individuals n n TABLE-1 JOHN MY-HAND ROLLING-EVENT-3

The Knowledge Base of a Description Logic n n Terminology (TBox) – hierarchy of concepts and roles Assertions (ABox) – axioms for individual objects

Benefits of Dividing the KB n n Reasoning is tractable due to sacrifice of expressiveness (Brachman and Levesque 1985) Philosophically ‘clean’: TBox (intensional knowledge, always true, doesn’t change, a priori) ABox (extensional knowledge, can change, a posteriori) Satisfiability of conceptualization (domain) is determined easily when only TBox is considered Conceptual modeling appears more intuitive

Syntax: Constructors n n n intersection (C D) : Round Flat Light value restriction (∀ R. C): ∀has. Hole. Container limited existential quantification (∃R. T): ∃has. Hole. T

Syntax: TBox Axioms n Definitions Ball Sphere Toy Box Container Cube Biped Animal =2 has. Legs Definitions are basic operation in TBox for deriving new concepts (other concepts are primitive).

Syntax: TBox Axioms (cont. ) n n n subsumption operator: ‘ ’ Table Furniture Human Animal Sphere 3 DShape Provide structure for TBox

Syntax: ABox Assertions n n n Concept assertions C(a): Person (JOHN) Table (TABLE-1) Tool (HAMMER-23) Role assertions R(a, b): Likes (JOHN, HAMMER-23) On (HAMMER-23, TABLE-1) Serves to link individuals in ABox to concepts in TBox

Note on T/ABox Relation n n TBox imposes selection restrictions on ABox assertions, e. g. , Eat(JOHN, TABLE-1) is not possible, because Edible(Table) is not in TBox

Informal Semantics n n n A concept C is a set of individuals {a, b, …} A role R is a relation between a pair of individuals or concepts. A conjoined concept C ⊔ D is both C and D.

Reasoning Tasks n n TBox categorization, satisfiability ABox consistency checking w. r. t. TBox

Ambiguity in a DL System n n More than one referent concept in TBox if a word W represents concept C and concept D, and C and D are disjoint, then W is ambiguous Represents(‘edge’, Linear. Boundary) Represents(‘edge’, 2 DSurface)

Consistency Checking for Determining Lexical Ambiguity n Recall that ‘box’ is ambiguous, as in ‘Check the box if you are a student. ’ 2 DObject(Box-34) 3 DObject(Box-34) n Disjoint (2 DObject, 3 DObject)

Consistency Checking for Resolving Ambiguity n n n The ball is on the edge of the table. Ball can’t be in two places. Only one semantic representation obtains from the TBox.

Conclusion n n Word sense disambiguation is challenge to NLP can benefit from a knowledge-rich approach. A combination of visual and other commonsense assertions can enrich the lexicon. Description logic provide a computationally tractable solution.