Lingkaran dan Lingkaran Singgung Suatu lingkaran yang berpusat

Lingkaran dan Lingkaran Singgung

Suatu lingkaran yang berpusat di O(0, 0). Mempunyai jari-jari 4 cm. Sebuah titik A(4, 0) dan B(-4, 0) terletak pada lingkaran. Sebuah garis yang menghubungkan titik B dengan titik C(0, -4) dilukis pada lingkaran tersebut.
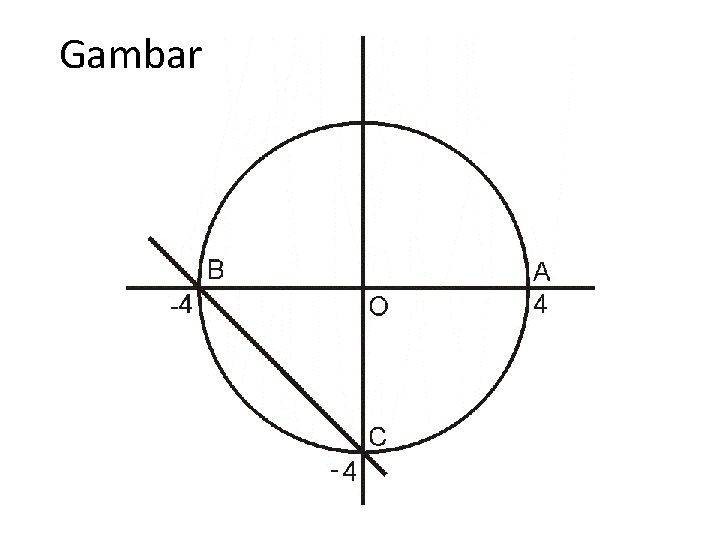
Gambar
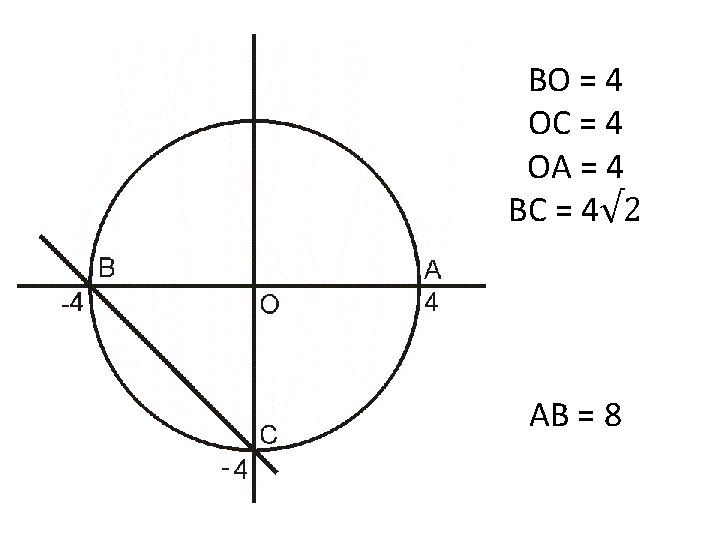
BO = 4 OC = 4 OA = 4 BC = 4√ 2 AB = 8
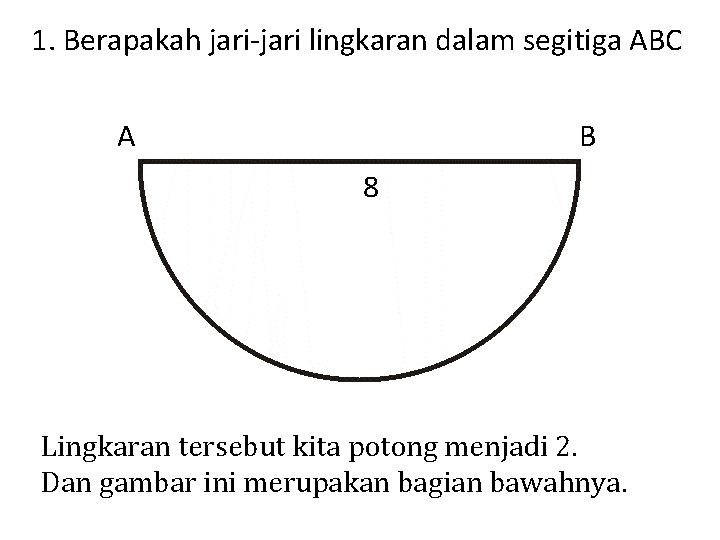
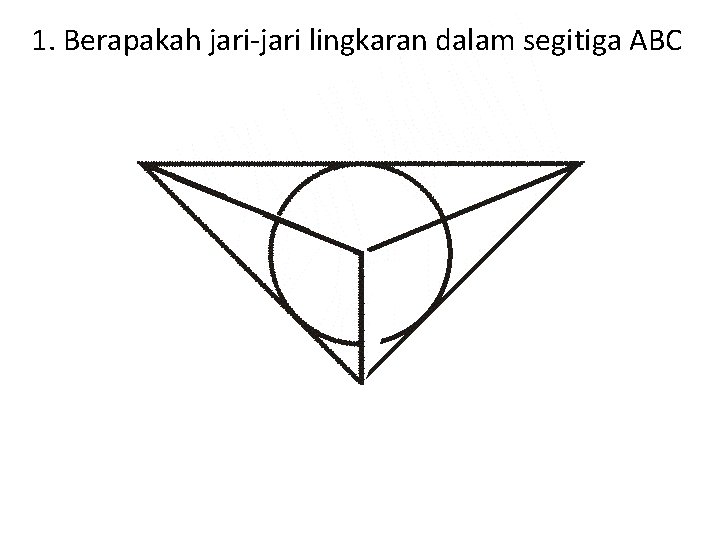
1. Berapakah jari-jari lingkaran dalam segitiga ABC A B 8 Lingkaran tersebut kita potong menjadi 2. Dan gambar ini merupakan bagian bawahnya.
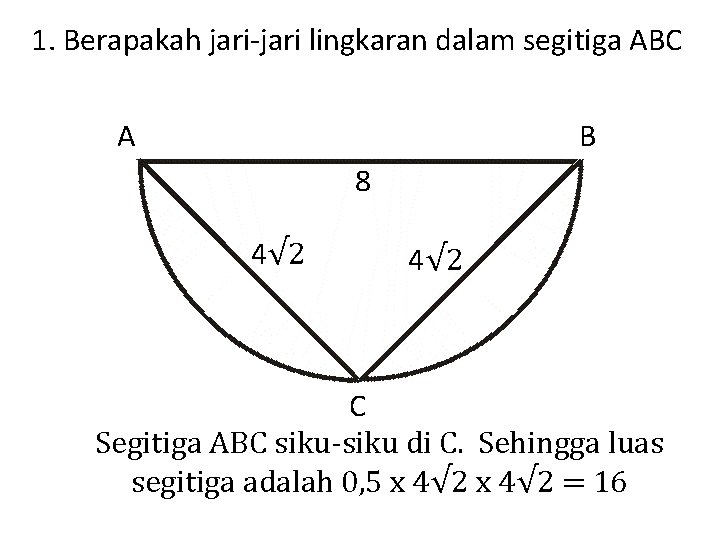
1. Berapakah jari-jari lingkaran dalam segitiga ABC A B 8 4√ 2 C Segitiga ABC siku-siku di C. Sehingga luas segitiga adalah 0, 5 x 4√ 2 = 16
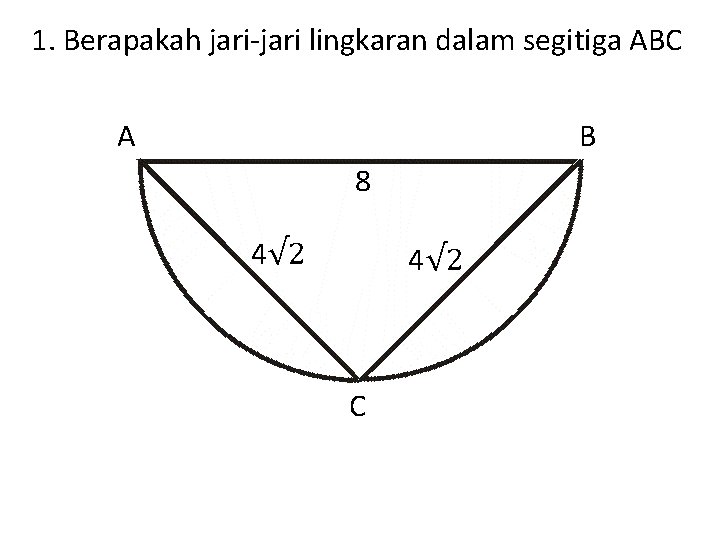
1. Berapakah jari-jari lingkaran dalam segitiga ABC A B 8 4√ 2 C
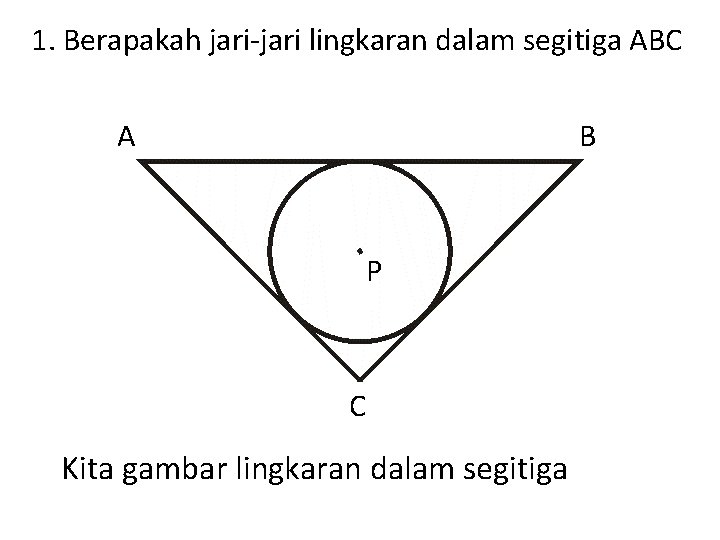
1. Berapakah jari-jari lingkaran dalam segitiga ABC A B P C Kita gambar lingkaran dalam segitiga
1. Berapakah jari-jari lingkaran dalam segitiga ABC A B P C
1. Berapakah jari-jari lingkaran dalam segitiga ABC A B P C
1. Berapakah jari-jari lingkaran dalam segitiga ABC
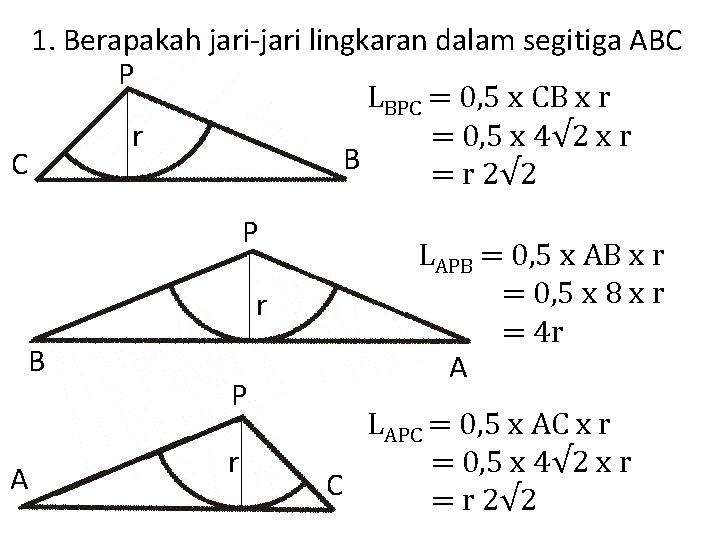
1. Berapakah jari-jari lingkaran dalam segitiga ABC P LBPC = 0, 5 x CB x r = 0, 5 x 4√ 2 x r r B C = r 2√ 2 P r B A P r LAPB = 0, 5 x AB x r = 0, 5 x 8 x r = 4 r A LAPC = 0, 5 x AC x r = 0, 5 x 4√ 2 x r C = r 2√ 2
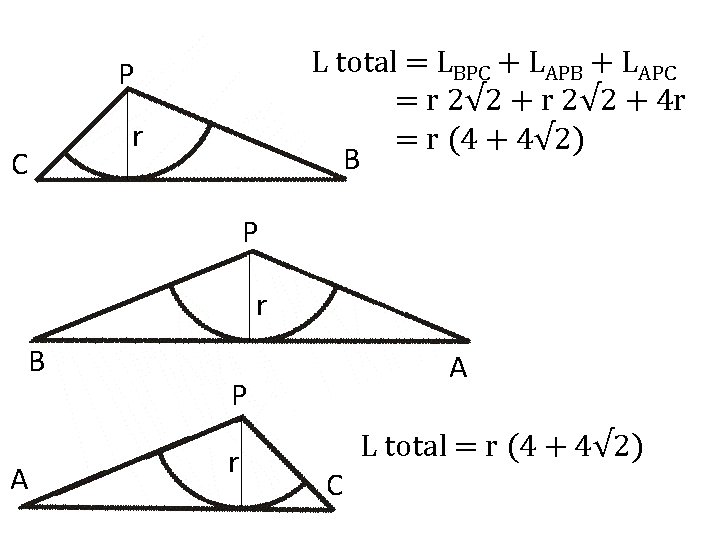
L total = LBPC + LAPB + LAPC = r 2√ 2 + 4 r = r (4 + 4√ 2) B P C r P r B A A P r L total = r (4 + 4√ 2) C

Di awal kita sudah menemukan bahwa luas segitiga ABC = 16 Dan tadi ditemukan luas = r (4 + 4√ 2) Sehingga, 16 = r (4 + 4√ 2) 16 r= (4 + 4√ 2)
2.
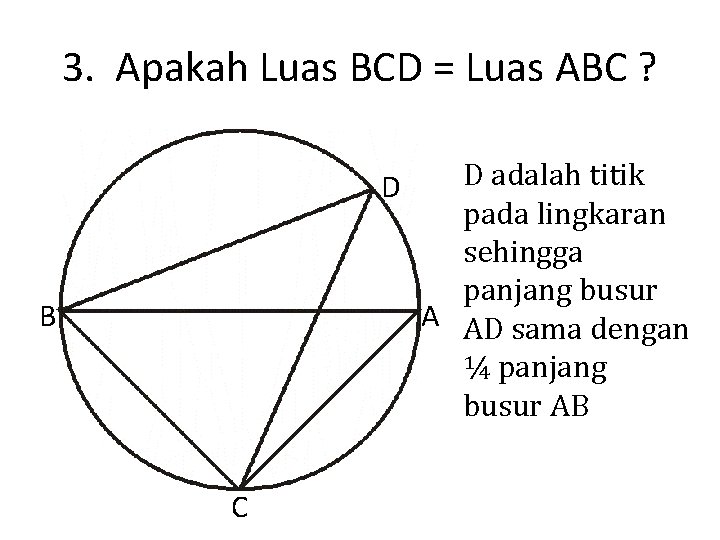
3. Apakah Luas BCD = Luas ABC ? D B C D adalah titik pada lingkaran sehingga panjang busur A AD sama dengan ¼ panjang busur AB
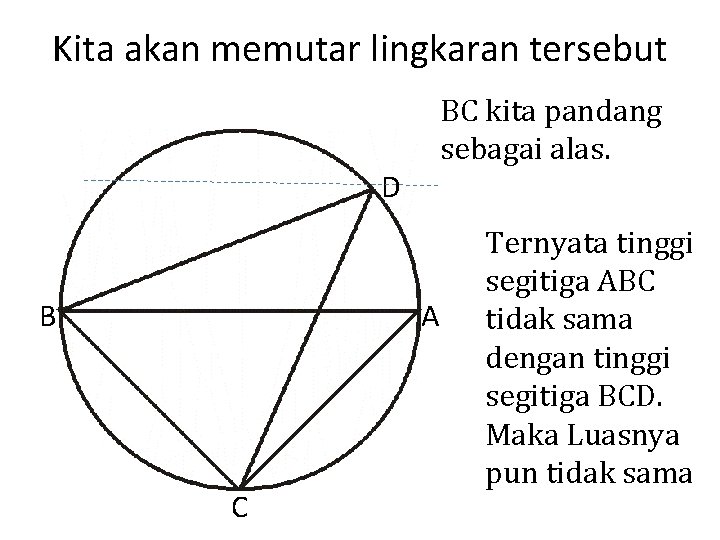
Kita akan memutar lingkaran tersebut BC kita pandang sebagai alas. D B A C Ternyata tinggi segitiga ABC tidak sama dengan tinggi segitiga BCD. Maka Luasnya pun tidak sama

4. Jika ra merupakann jari-jari lingkaran yang menyinggung sisi BC, perpanjangan garis BC dan perpanjangan garis AC. rb adalah jari-jari lingkaran yang menyinggung sisi AC, perpanjangan garis BC dan perpanjangan garis BA. rc adalah jari-jari lingkaran yang menyinggung sisi BA, perpanjangan garis BC dan perpanjangan garis AC. rd adalah jari-jari lingkaran dalam segitiga ABC Tunjukkan bahwa ra rb rc = 1/rd
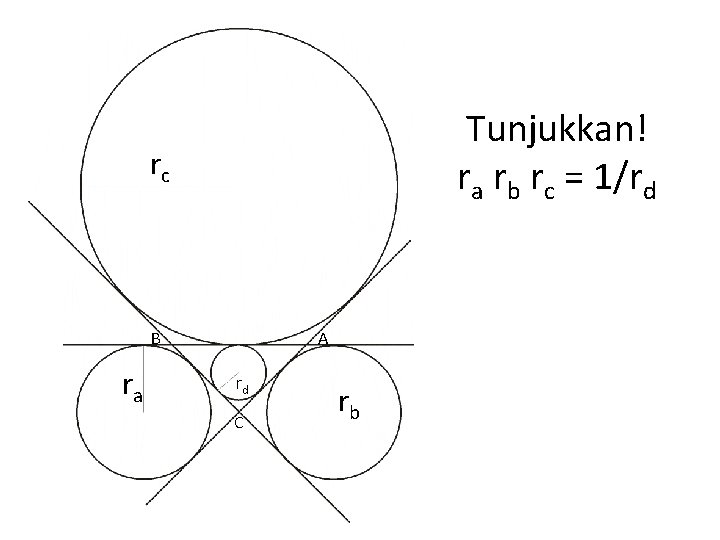
Tunjukkan! ra rb rc = 1/rd rc B ra A rd C rb
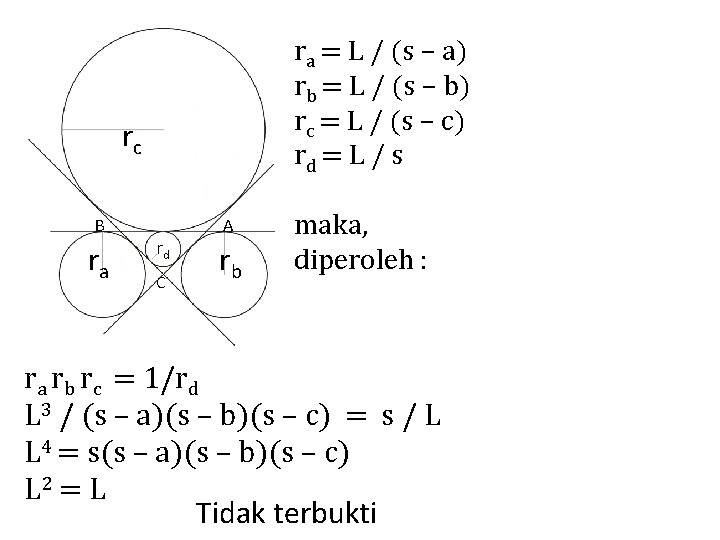
ra = L / (s – a) rb = L / (s – b) rc = L / (s – c) rd = L / s rc B ra rd C A rb maka, diperoleh : ra rb rc = 1/rd L 3 / (s – a)(s – b)(s – c) = s / L L 4 = s(s – a)(s – b)(s – c) L 2 = L Tidak terbukti
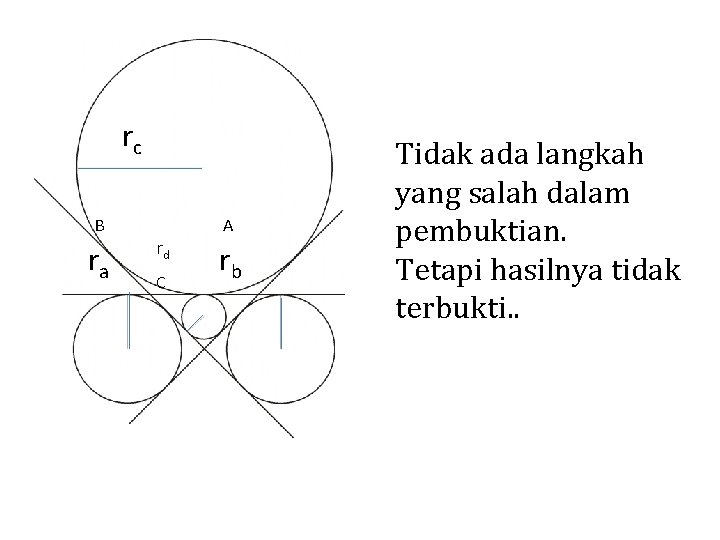
rc B ra rd C A rb Tidak ada langkah yang salah dalam pembuktian. Tetapi hasilnya tidak terbukti. .
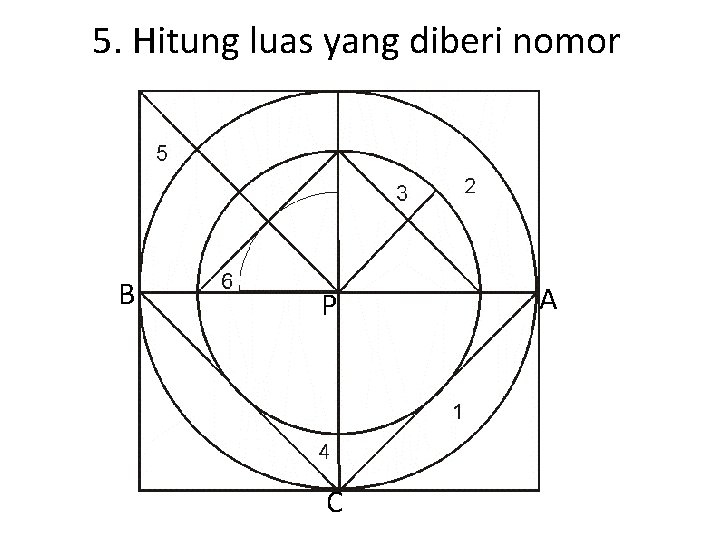
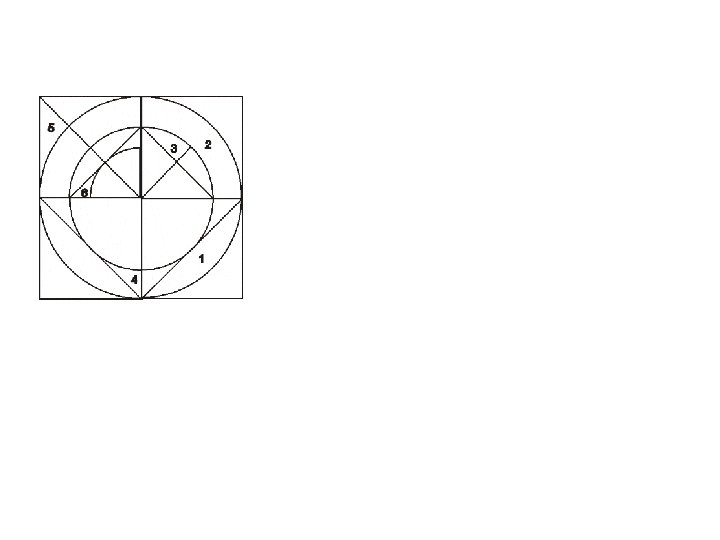
5. Hitung luas yang diberi nomor B P C A
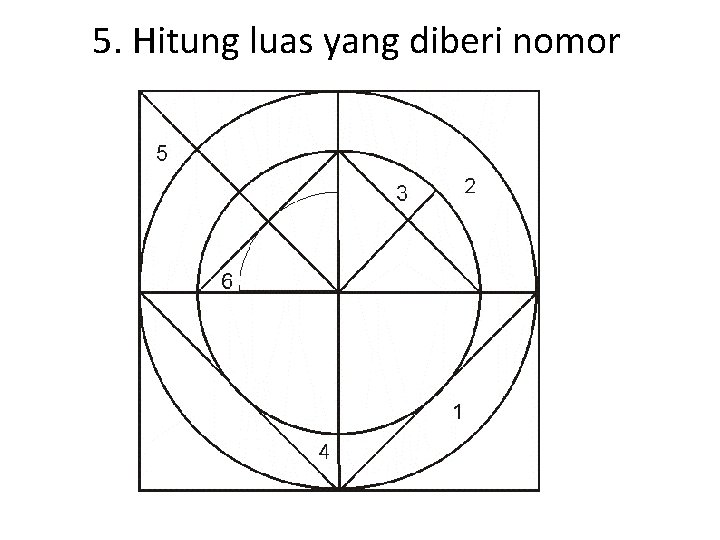
5. Hitung luas yang diberi nomor
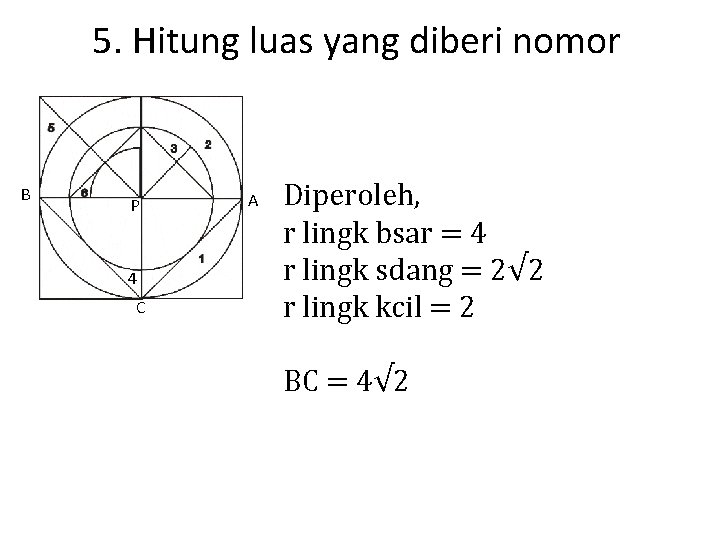
5. Hitung luas yang diberi nomor B P 4 C A Diperoleh, r lingk bsar = 4 r lingk sdang = 2√ 2 r lingk kcil = 2 BC = 4√ 2
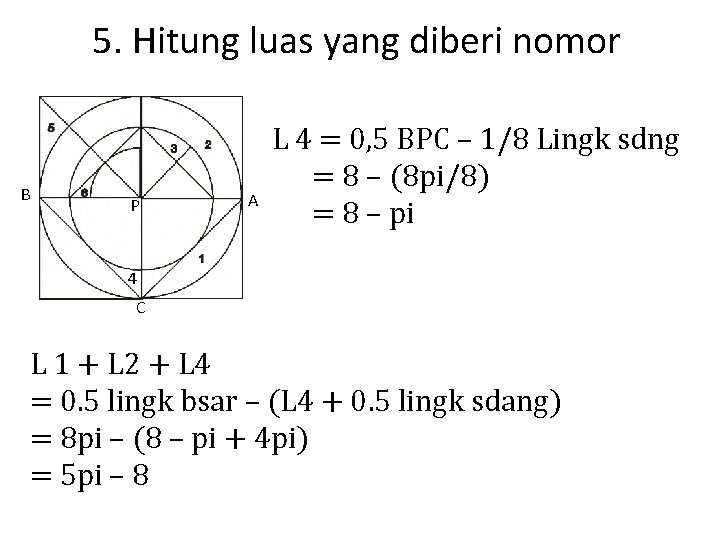
5. Hitung luas yang diberi nomor B P A L 4 = 0, 5 BPC – 1/8 Lingk sdng = 8 – (8 pi/8) = 8 – pi 4 C L 1 + L 2 + L 4 = 0. 5 lingk bsar – (L 4 + 0. 5 lingk sdang) = 8 pi – (8 – pi + 4 pi) = 5 pi – 8
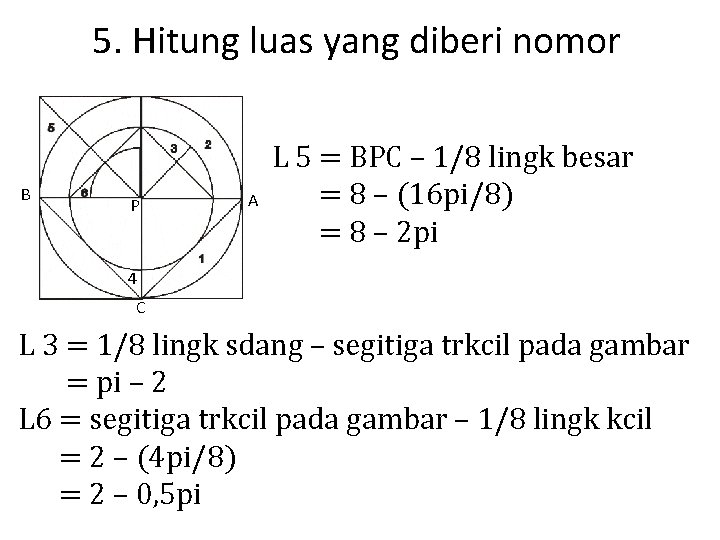
5. Hitung luas yang diberi nomor B P A L 5 = BPC – 1/8 lingk besar = 8 – (16 pi/8) = 8 – 2 pi 4 C L 3 = 1/8 lingk sdang – segitiga trkcil pada gambar = pi – 2 L 6 = segitiga trkcil pada gambar – 1/8 lingk kcil = 2 – (4 pi/8) = 2 – 0, 5 pi

5. Hitung luas yang diberi nomor B P A Luas Total adalah L 1 + L 2 + L 3 + L 4 + L 5 + L 6 4 C L Total = (8 – pi) + (5 pi – 8) + (8 – 2 pi)+(pi – 2)+ (2 – 0, 5 pi) L total = 8 + 2, 5 pi

h
- Slides: 29