Lineshape function If one performs a spectral analysis

深圳大学电子科学与技术学院 Lineshape function • If one performs a spectral analysis of the radiation emitted by spontaneous 2 1 transitions, one finds that the radiation is not strictly monochromatic (that is, of one frequency) but occupies a finite frequency bandwidth. The function describing the distribution of emitted intensity versus the frequency is referred to as the lineshape function (of the transition 2 1) and its arbitrary scale factor is usually chosen so that the function is normalized according to

深圳大学电子科学与技术学院 • We can consequently view as the a priori probability that a given spontaneous emission from level 2 to level 1 will result in a photon whose frequency is between and +d. • The separation between the two frequencies at which the lineshape function is down to half its peak value is referred to as the linewidth.

深圳大学电子科学与技术学院 • Another method of determining is to apply an electromagnetic field to the sample containing the atoms and then plot the amount of energy absorbed by 1 2 transitions as a function of the frequency. This function is again. • The fact that both the emission and the absorption are described by the same lineshape function can be verified experimentally, follows from basic quantum mechanical considerations.

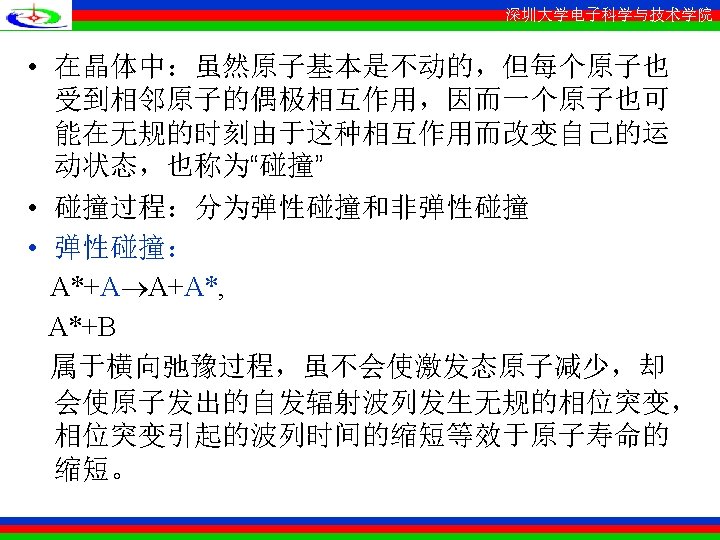
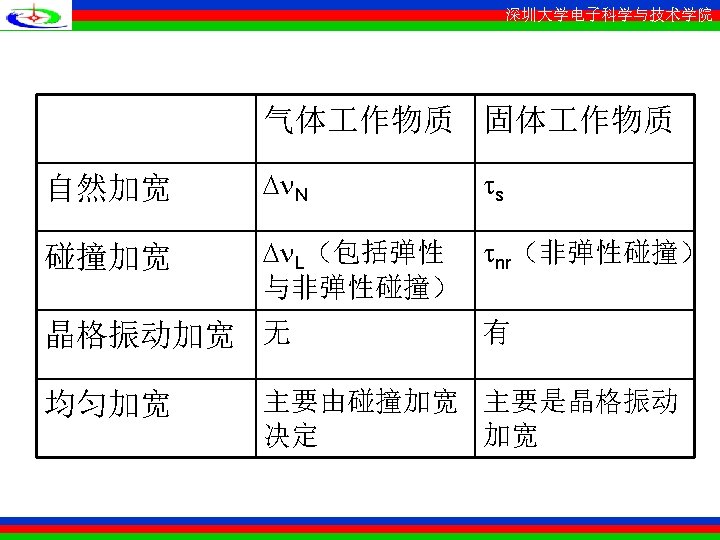
深圳大学电子科学与技术学院 • Curves with the function dependence of (4. 3. 5) are called Lorentzian. They occur often in physics and engineering, since they characterize the response of damped resonate systems. • The type of broadening (that is, the finite width of the emitted spectrum) describes above is called homogeneous broadening. It is characterized by the fact the spread of the response over a band ~ is characteristic of each atom in the sample. The function thus describes the response of any of the atoms which are indistinguishable.

深圳大学电子科学与技术学院 • Homogenous broadening is due most often to the finite interaction lifetime of the emitting or absorbing atoms. Some of the most common mechanisms are: • 1 The spontaneous lifetime of the excited state • 2 Collision of an atom embedded in a crystal with a phonon. This may involve the emission or absorption of acoustic energy. Such a collision does not terminate the lifetime of the atom in its absorbing or emitting state.

深圳大学电子科学与技术学院 It does interrupt, however, the relative phase between the atomic oscillation and that of the field, thus causing a broadening of the response where now represents the mean uninterrupted interaction time. • 3 Pressure broadening of atoms in a gas. At sufficiently high atomic densities the collisions between atoms become frequent enough that lifetime termination and phase interruption as in the preceding mechanism dominate the broadening mechanism.

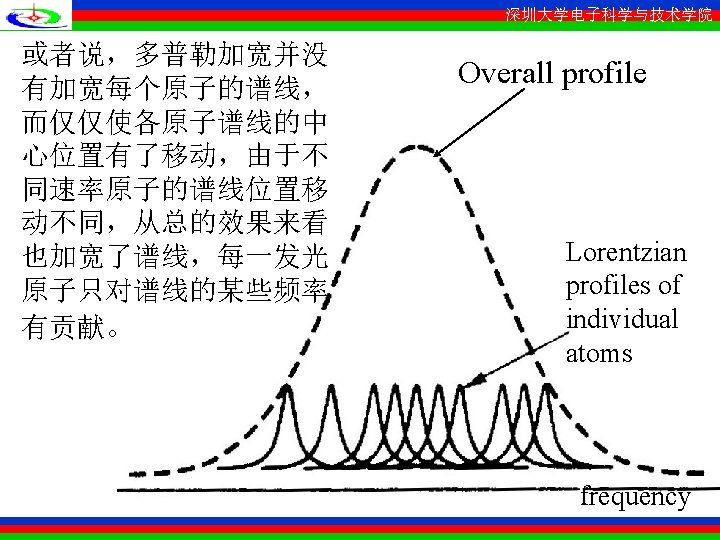
深圳大学电子科学与技术学院 • There are, however, many physical situations in which the individual atoms are distinguishable, each having a slightly different transition frequency 0. If one observes, in this case, the spectrum of the spontaneous emission, its spectral distribution will reflect the spread in the individual transition frequencies and not the broadening due to the finite lifetime of the excited state. This type of broadening, referred to as inhomogeneous.

深圳大学电子科学与技术学院 • Consider an atom with a transition frequency where 2 and 1 refer to the upper and lower laser levels, respectively. Let the component of the velocity of the atom parallel to the wave (its frequency of ) propagation direction be z. An atom moving with a constant velocity z will thus “see” a Doppler-shifted frequency

深圳大学电子科学与技术学院 • The condition for the maximum strength of interaction (that is, emission or absorption) between the moving atom and the wave is that the apparent (Doppler) frequency D“seen” by the atom be equal to the atomic resonant frequency 0

深圳大学电子科学与技术学院 • or reversing the argument, a wave of frequency moving through an ensemble of atoms will “seek out” and interact most strongly with those atoms whose velocity component z satisfies where the approximation is valid for z<<c

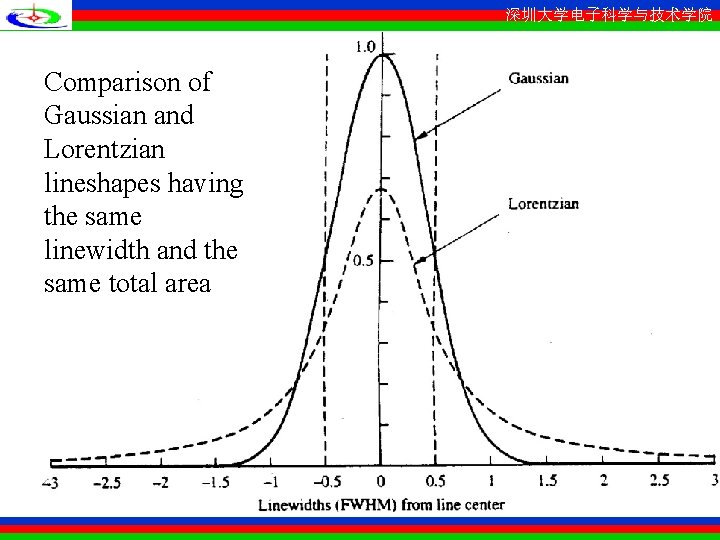
深圳大学电子科学与技术学院 Comparison of Gaussian and Lorentzian lineshapes having the same linewidth and the same total area