Lines Angles and Triangles Special Segments in Triangles

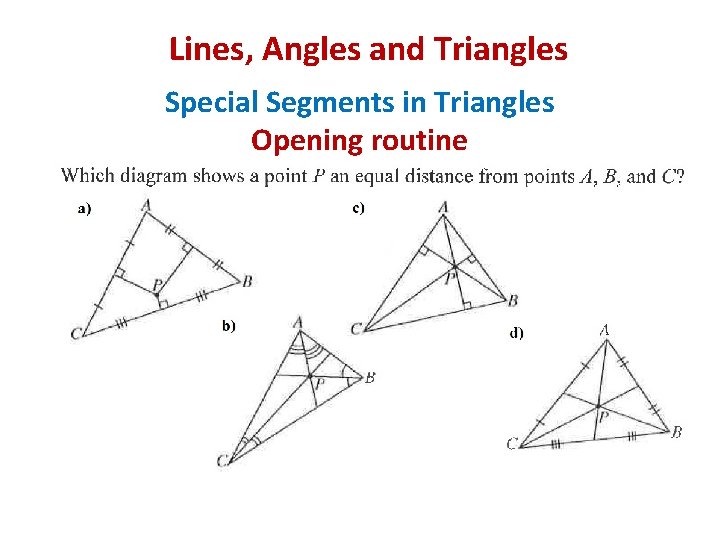
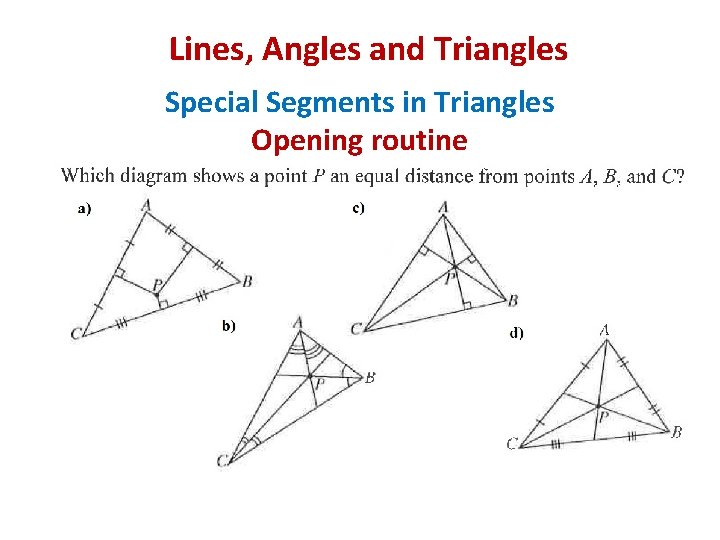
Lines, Angles and Triangles Special Segments in Triangles Opening routine

Lines, Angles and Triangles Special Segments in Triangles Opening routine

Lines, Angles and Triangles Special Segments in Triangles Opening routine

Lines, Angles and Triangles Special Segments in Triangles Opening routine

Lines, Angles and Triangles Special Segments in Triangles Opening routine

Topic III: Lines, Angles and Triangles

Lines, Angles and Triangles Special Segments in Triangles Objectives: Identify and use perpendicular bisectors, angle bisectors, medians and altitudes in triangles. Essential Question: How can you use the points of concurrency in triangles?

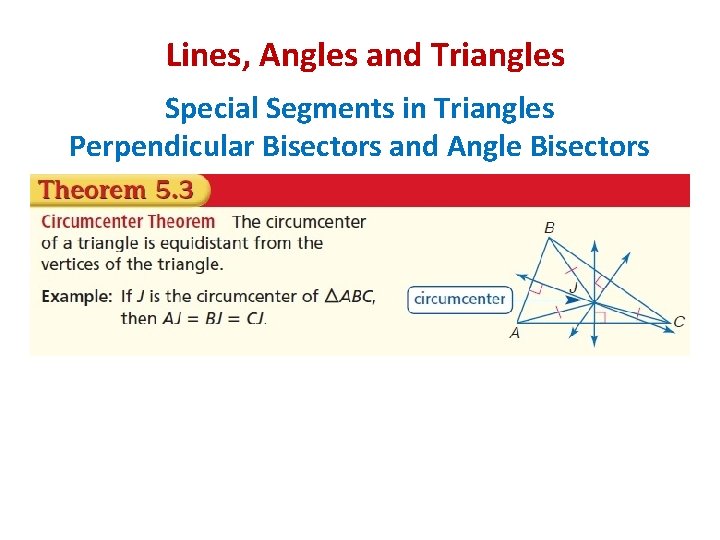
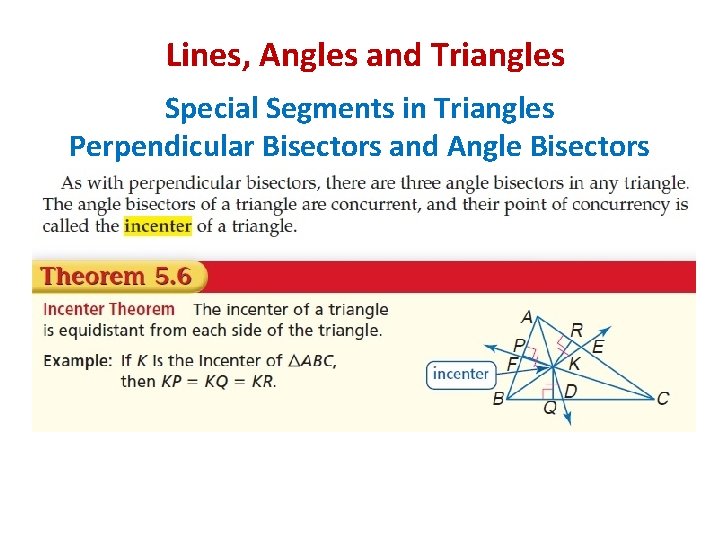
Lines, Angles and Triangles Special Segments in Triangles Perpendicular Bisectors and Angle Bisectors Vocabulary Perpendicular bisector: Is a segment that passes by the midpoint of a side and is perpendicular to that side. They are concurrent. Circumcenter: Is the point of concurrency of the perpendicular bisectors of a triangle. It is equidistant from the vertices of the triangle.

Lines, Angles and Triangles Special Segments in Triangles Vocabulary Angle bisector: Is a bisector to any of the angles of the triangle. Any point on the angle bisector is equidistant from the sides of the angle. They are concurrent. Incenter: Is the point of concurrency of the angle bisectors. It is equidistant from the sides of the triangle.

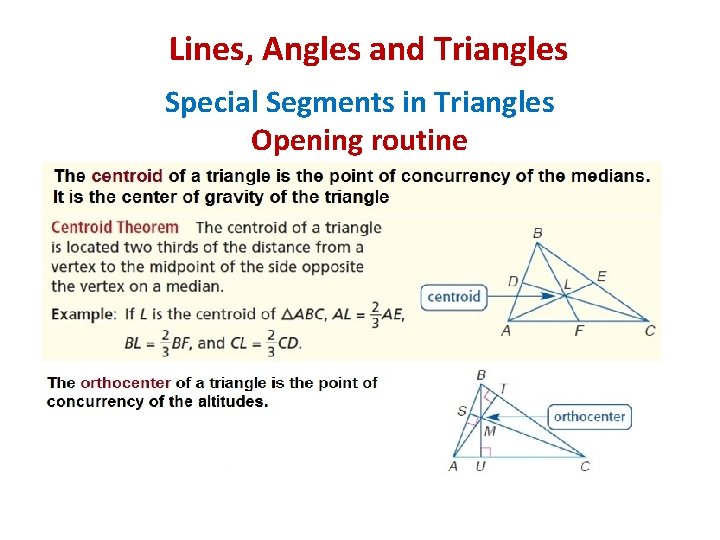
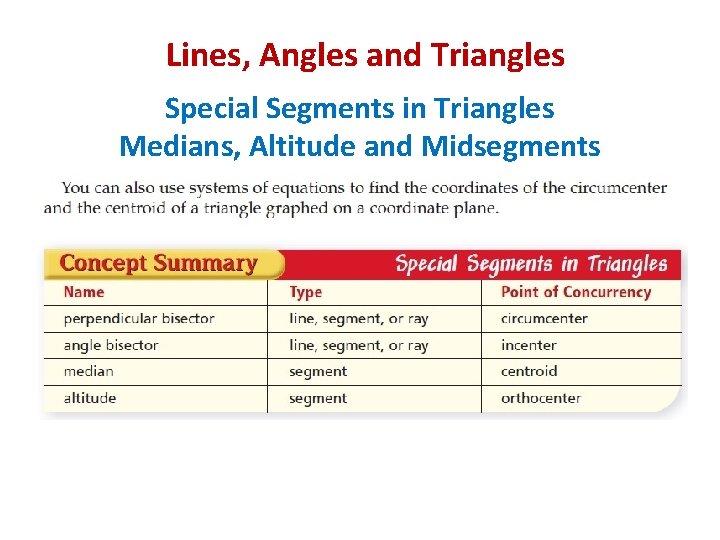
Lines, Angles and Triangles Special Segments in Triangles Vocabulary Median: Is a segment whose endpoints are a vertex of a triangle and the midpoint of the side opposite the vertex. They are concurrent. Centroid: Is the point of concurrency of the medians of a triangle. It is the point of balance of any triangle.

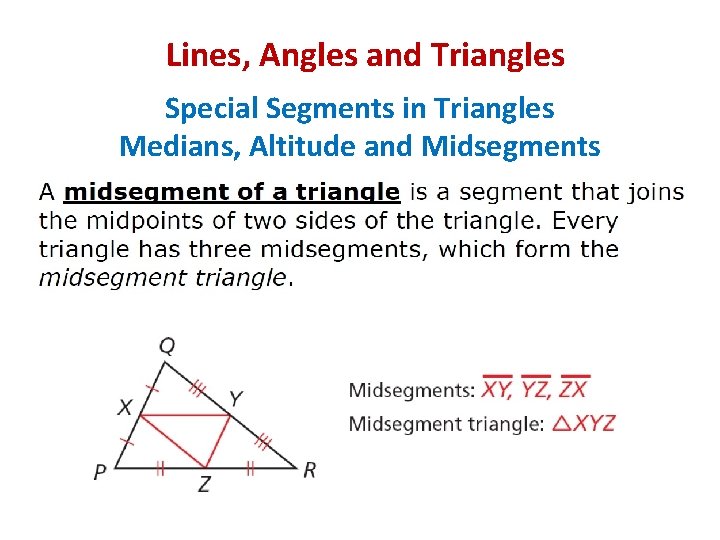
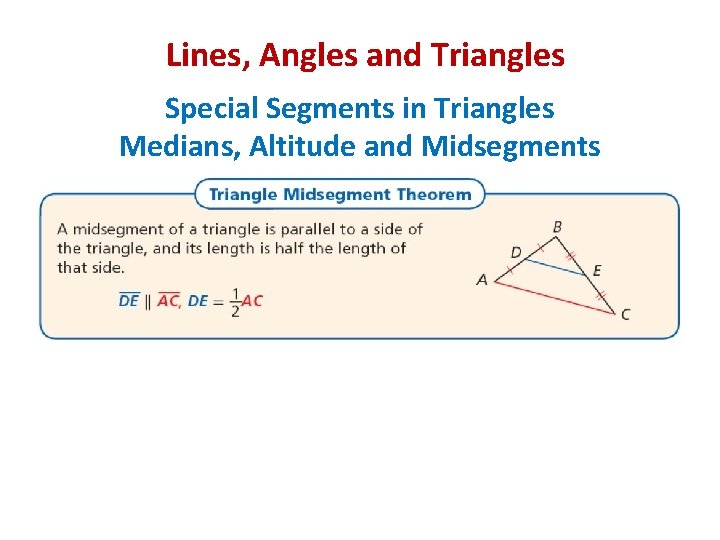
Lines, Angles and Triangles Special Segments in Triangles Vocabulary Altitude: Is a segment that joins a vertex of a triangle with the opposite side and is perpendicular to that side. Orthocenter: Is the point of concurrency of the altitudes of a triangle. Midsegment: Is a segment that joins the midpoints of two sides of the triangle. Every triangle has three midsegments, which form the midsegment triangle.

Lines, Angles and Triangles Special Segments in Triangles Perpendicular Bisectors and Angle Bisectors

Lines, Angles and Triangles Special Segments in Triangles Perpendicular Bisectors and Angle Bisectors

Lines, Angles and Triangles Special Segments in Triangles Perpendicular Bisectors and Angle Bisectors

Lines, Angles and Triangles Special Segments in Triangles Perpendicular Bisectors and Angle Bisectors

Lines, Angles and Triangles Special Segments in Triangles Perpendicular Bisectors and Angle Bisectors

Lines, Angles and Triangles Special Segments in Triangles Medians, Altitude and Midsegments

Lines, Angles and Triangles Special Segments in Triangles Medians, Altitude and Midsegments

Lines, Angles and Triangles Special Segments in Triangles Medians, Altitude and Midsegments

Lines, Angles and Triangles Special Segments in Triangles Medians, Altitude and Midsegments

Lines, Angles and Triangles Special Segments in Triangles Medians, Altitude and Midsegments

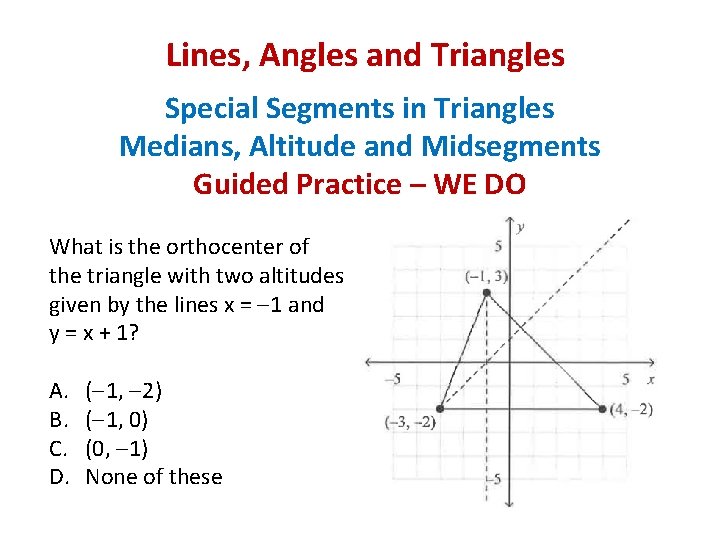
Lines, Angles and Triangles Special Segments in Triangles Medians, Altitude and Midsegments Guided Practice – WE DO What is the orthocenter of the triangle with two altitudes given by the lines x = 1 and y = x + 1? A. B. C. D. ( 1, 2) ( 1, 0) (0, 1) None of these

Lines, Angles and Triangles Special Segments in Triangles Independent Practice - YOU DO Worksheet “Review Topic III” Exercises from 1 to 20

Quadrilaterals and Coordinates Proof for Parallelograms Closure Essential Question: What criteria can be used in a coordinate proof to determine of a quadrilateral is a parallelogram?