Linerny regresn model Damodar Gujarati Econometrics by Example

Lineárny regresný model Damodar Gujarati Econometrics by Example

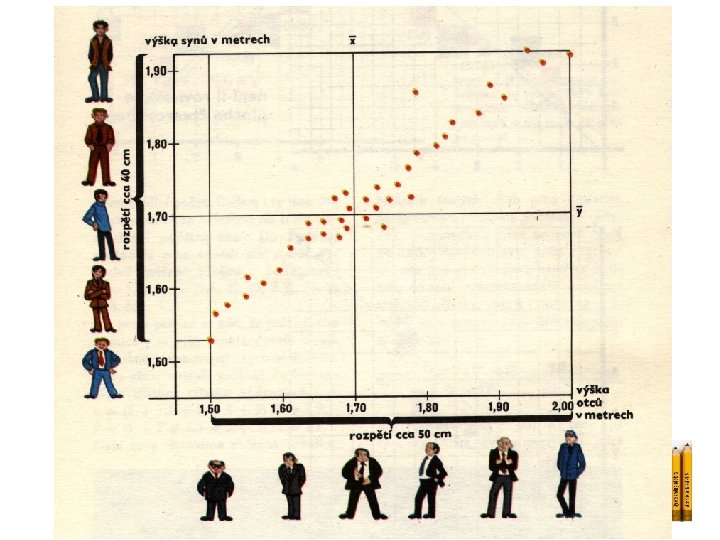
2

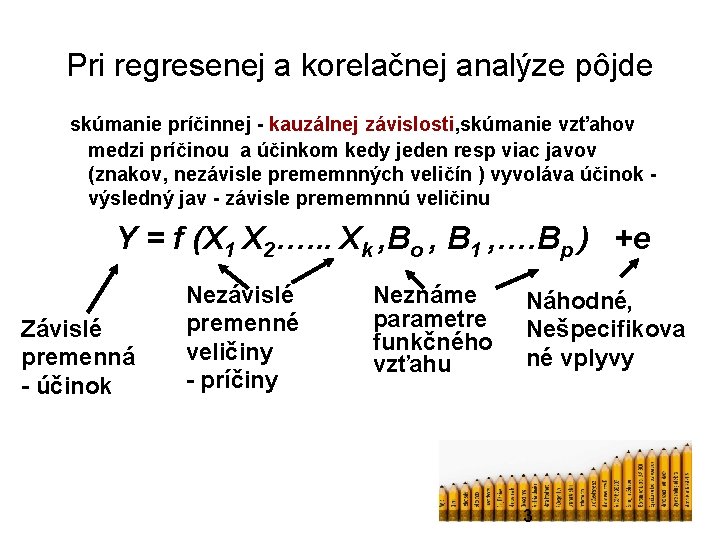
Pri regresenej a korelačnej analýze pôjde skúmanie príčinnej - kauzálnej závislosti, skúmanie vzťahov medzi príčinou a účinkom kedy jeden resp viac javov (znakov, nezávisle prememnných veličín ) vyvoláva účinok výsledný jav - závisle prememnnú veličinu Y = f (X 1 X 2…. . . Xk , Bo , B 1 , …. Bp ) +e Závislé premenná - účinok Nezávislé premenné veličiny - príčiny Neznáme parametre funkčného vzťahu Náhodné, Nešpecifikova né vplyvy 3

Príklad zdanlivej korelácie Jedna z preslávených zdanlivých korelácií : ak sa dĺžka sukní skracuje kurzy akcií stúpajú. Odhliadnúc od toho, že to nie vždy platí, išlo by skutočneo zdanlivú, alebo nezmyselnú koreláciu 4

Damodar Gujarati Econometrics by Example

Opakom štatistickej závislosti je funkčná závislosť Y = f(X 1 X 2…. . . Xk , Bo , B 1 , …. , Bp) kedy je závisle prememnná veličina jednoznačne určená funkčným vzťahom, príklady z fyziky, chémie - takýto druh vzťahov nie je predmetom štatistického skúmania 6

Regresná analýza – regresná úloha (RÚ) jej podstatou je a) nájsť funkčný vzťah podľa ktorého sa mení závislé premenná so zmenou nezávisle premenných - nájsť vhodnú regresnú funkciu. b) Súčasne je potrebné odhadnúť parametre regresnej funkcie. 7

Lineárny regresný model Ø Všeobecná forma viacnásobného regresného modelu: Yi = B 1 + B 2 X 2 i + B 3 X 3 i + … + Bk. Xki + ui Ø Skrátená forma: Yi = BX + ui Ø Y vysvetlovaná premenná (regressand), X je vektor vysvetlujúcich premenných (regressorov), and u je náhodná chyba (reziduá). Damodar Gujarati Econometrics by Example

Regresné koeficienty Ø B 1 je lokujúca konštanta - vyjadruje očakávanú úroveň závislé premennej pri nulovej hodnote nezávisle premennej Ø B 2 až Bk sú regresné koeficienty (smernice) Ø Každý regresný koeficient meria (parciálnu) mieru zmeny v priemernej hodnote Y pri jednotkovej zmene v hodnote vysvetlujúcej premennej, ceteris paribus. Damodar Gujarati Econometrics by Example

Typy údajov Ø Časové rady ØSúbor pozorovaní ktoré nadobúda premenná v rôznych časových obdobiach ako napríklad denné (napr. ceny akcií), Týždenné (napr. ponuka peňazí), mesačné (napr. miera nezamestnanosti), kvartálne čiže štvrťročné (napr. HDP), ročné (napr. štátny rozpočet), päťročné (napr. sčítanie výrobcov), alebo desaťročné (napr. sčítanie obyvateľov). Damodar Gujarati Econometrics by Example

Typy údajov Ø Prierezové údaje ØÚdaje o jednej alebo viacerých premenných získané v jednom bode v čase. ØPríkladom sú napríklad sčítanie obyvateľov vykonávané štatistickým úradom, rôzne prieskumy preferencií, či namerané teploty v danom čase na rôznych miestach. Damodar Gujarati Econometrics by Example

Typy údajov Ø Panelové, longitudálne alebo mikropanelové údaje ØKombinujú prvky oboch predchádzajúcich, tak časových radov ako aj prierezových údajov ØRovnaké prierezové jednotky sú sledované v čase Damodar Gujarati Econometrics by Example

Metóda najmenších štvorcov Ø Metóda najmenších štvorcov (MNŠ) neminimalizuje sumu odchýlok, ale minimalizuje sumu štvorcov odchýlok: Ø Pre získanie regresných koeficientov sú parciálne derivácie podla jednotlivých regresných koeficientov dané do rovnosti s nulou. Damodar Gujarati Econometrics by Example

Klasický lineárny regresný model Ø Predpoklady klasického lineárneho regresného modelu (CLRM): Ø A-1: Model je lineárny v parametroch. Ø A-2: Vysvetľujúce premenné sú nestochastické a konštantné v opakovaných výberoch. Ø A-3: Pre dané X, stredná hodnota reziduí je 0, alebo E(ui |X) = 0. Damodar Gujarati Econometrics by Example

Klasický lineárny regresný model Ø Predpoklady klasického lineárneho regresného modelu: Ø A-4: Homoskedastický, alebo konštantný rozptyl ui, zapísané ako var(ui|X) = σ2. Ø A-5: Žiadna autokorelácia rezíduí, alebo cov(ui, uj|X) = 0, i ≠ j. Ø A-6: Žiadna multikolinearita, teda žiadna perfektná lineárna závislosť medzi vysvetľujúcimi premennými. Ø A-7: Žiadne chyby špecifikácie. Damodar Gujarati Econometrics by Example

GAUSS-MARKOV TEORÉM Ø Na základe predpokladov A-1 až A-7, dáva MNŠ najlepšie lineárne nevychýlené odhady ak: Ø(1) Estimátory sú lineárnou funkciou závisle premennej Y. Ø(2) Estimátory sú nevychýlené; pri opakovanom použití metódy dosahujú odhady svoje skutočné hodnoty. Ø(3) V kategórii lineárnych odhadov, estimátory majú estimátory získané metódou najmenších štvorcov minimálny rozptyl; teda sú efektívnymi alebo aj „najlepšími“ odhadmi. Damodar Gujarati Econometrics by Example

Testovanie hypotéz: t TEST Ø Testujeme nasledujúce hypotézy: H 0: Bk = 0 H 1: Bk ≠ 0 vypočítame testovaciu štatistiku podľa nasledujúceho vzorca a použijeme tabuľky studentovho rozdelenia aby sme získali t kritické s n-k stupňami voľnosti pre danú hladinu významnosti (alebo α, rovné 10%, 5%, alebo 1%): Pokiaľ je táto hodnota vačšia ako t kritické, zamietneme H 0. Damodar Gujarati Econometrics by Example

Testovanie hypotéz: t TEST Ø Alternatívnou metódou je určiť, či sa v intervale spolahlivosti nachádza 0: Ø Pokiaľ nula leží v intervale spoľahlivosti nemôžeme zamietnuť H 0. Ø p-value označuje presnú hladinu významnosti, alebo najnižšiu hladinu významnosti na ktorej môžeme zamietnuť H 0. Damodar Gujarati Econometrics by Example

Koeficient determinácie, R 2 Ø Koeficient determinácie je všeobecnou mierou presnosti modelu. Ø Percentuálny podiel celkovej variability závislej premennej ktorá je vysvetlená nezávislými premennými. Ø Nadobúda hodnoty medzi 0 a 1 <0% , 100%>. Ø Nech: Ø Potom: Damodar Gujarati Econometrics by Example

Index korelácie a index determinácie V základnom súbore Iyx odhadom z výberových údajov je iyx est Iyx = iyx. Princíp spočíva v rozklade variability závisle premennne Y Celková variabilita závisle premennej Variabilita závisle premennej vysvetlená regresnou funkciou Variabilita nevysvetlená regresnou funkciou - reziduálna variabilita 20

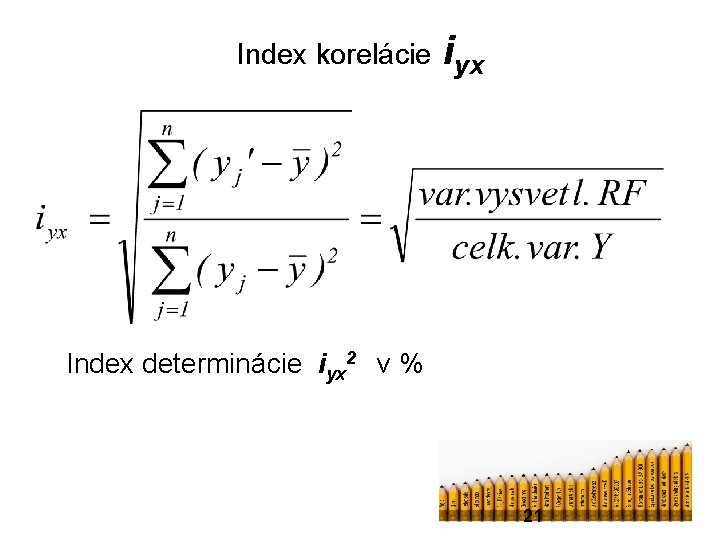
Index korelácie iyx Index determinácie iyx 2 v % 21

Testovanie hypotéz: F TEST Ø Testovanie nasledujúcich hypotéz je ekvivalentné testovaniu hypotéz že sú všetky regresné koeficienty rovné 0: H 0: R 2 = 0 H 1: R 2 ≠ 0 Ø Vypočítame nasledujúcí vzťah a použijeme tabuľky F rozdelenia pre získanie kritickej F hodnoty s k-1 stupňami voľnosti v čitateli a n-k stupňami voľnosti v menovateli pre danú hladinu významnosti: Pokiaľ je vypočítaná hodnota vyššia ako F kritické zamietame, H 0. Damodar Gujarati Econometrics by Example

Funkčné formy regresných modelov Damodar Gujarati Econometrics by Example

LOG-LINEÁRNY, LOG-LOG, ALEBO MODEL S KONŠTANTNOU ELASTICITOU Ø Cobb-Douglasova produkčná funkcia: môže byť transformovaná na lineárny tvar po zlogarigmovaní oboch strán: Ø Regresné koeficienty môžu byť interpretované ako elasticity. Ø Ak (B 2 + B 3) = 1, konštantné výnosy z rozsahu. Ø Ak (B 2 + B 3) > 1, rastúce výnosy z rozsahu. Ø Ak (B 2 + B 3) < 1, klesajúce výnosy z rozsahu. Damodar Gujarati Econometrics by Example

LOG-LIN alebo rastový model Ø Miera rastu reálneho GDP: môže byť transformovaný na lineárny po zlogaritmovaní oboch strán: Ø Pokiaľ B 1 = ln RGDP 1960 a B 2 = ln (l+r), môžeme to prepísať nasledovne: ln RGDPt = B 1 +B 2 t Ø B 2 je semi-elasticita, alebo aj okamžitá miera rastu. Ø Zložená miera rastu (r) je rovná (e. B 2 – 1). Damodar Gujarati Econometrics by Example

LIN-LOG MODEL Ø Lin-log má všeobecnú formu: Ø Všimnite si že B 2 je absolútnou zmenou v. Y zodpovedajúcou percentuálnej (alebo relatívnej) zmene v X Ø Ak X vzrastie o 100%, predikované Y vzrastie o B 2 jednotiek Ø Používané pri odhade Engelovej výdajovej funkcie: “Celkové výdavky vynaložené na potraviny rastú aritmetickou mierou zatial čo celkové výdavky rastú geometrickou mierou. ” Damodar Gujarati Econometrics by Example

Reciproký regresný model (hyperbola) Ø Všeobecná forma modelu: Ø Všimnite si že: Ø Ak X vzrastie nekonečne, člen asymptotickú hodnotu B 1. Ø Sklon sa vypočíta: dosiahne nulu a Y dosiahne limitnú teda Ø Platí teda, ak B 2 je pozitívne, sklon je negatívny, a pokiaľ B 2 je negatívne, sklon je pozitívny. Damodar Gujarati Econometrics by Example

POLYNOMICKÉ REGRESNÉ MODELY Ø Nasledujúci príklad modelu predikujúceho HDP je príklad kvadratickej funkcie, alebo vo všeobecnosti, polynóm druhého stupňa vysvetlujúcej premennej čas: Ø Sklon je nelineárny: Damodar Gujarati Econometrics by Example

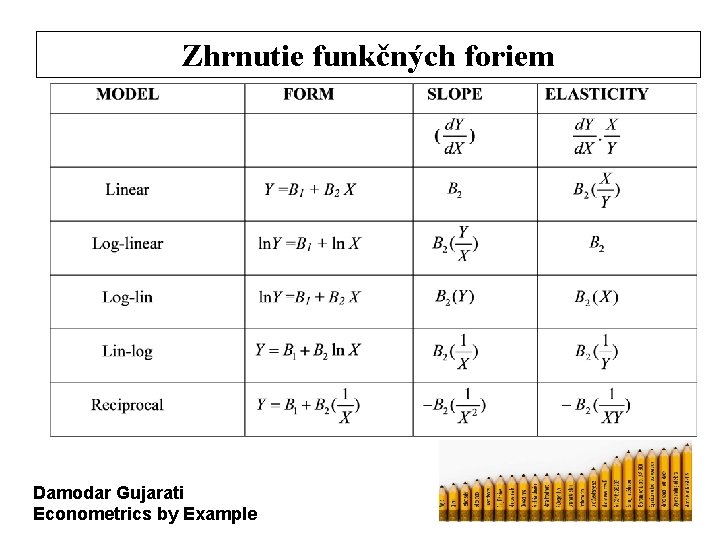
Zhrnutie funkčných foriem Damodar Gujarati Econometrics by Example

Štandardizované premenné Ø Problému s premennými meranými v rozdielnych jednotkách môžeme predísť ich vyjadrením v štandardizovanom tvare: kde SY a SX sú výberové štandardné odchýlky a sú výberové priemery Y a X Ø Stredná hodnota štandardizovanej premennej je vždy nulová a jej štandardná odchýlka je vždy 1. Damodar Gujarati Econometrics by Example

Miery kvality modelu Ø R 2: Meria podiel variability závisle premennej ktorá je vysvetlená nezávisle premennými, resp. modelom. Ø Korigovaný R 2: označuje sa ako , zohľadňuje počet vysvetľujúcich premenných v modeli: Ø Akaikeho informačné kritérium (AIC): Tvrdšie penalizuje pridanie ďalších premenných do modelu: Ø Zvyčajne je vybratý model s najnižšou hodnotou AIC. Ø Schwarzove informačné kritérium (SIC): Alternatíva k AIC kritériu vyjadrená ako: Ø Penalizačný faktor je prísnejší ako pri AIC. Damodar Gujarati Econometrics by Example