LINER FUNKTIONE R MATEMATIK A HVAD ER EN
















- Slides: 20

LINEÆR FUNKTIONE R MATEMATIK A

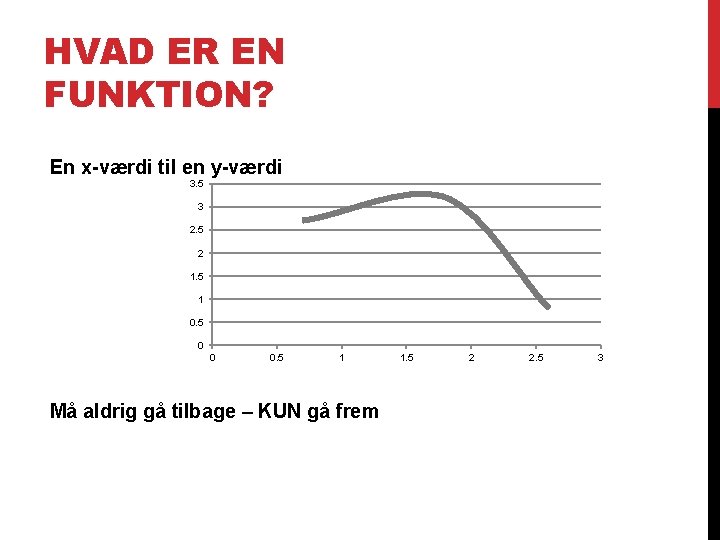
HVAD ER EN FUNKTION? En x-værdi til en y-værdi 3. 5 3 2. 5 2 1. 5 1 0. 5 0 0 0. 5 1 Må aldrig gå tilbage – KUN gå frem 1. 5 2 2. 5 3

LINEÆR FUNKTION Generelle forskrift for en lineær funktion: f(x)=ax+b ax=hældningen b=skæring i y-aksen

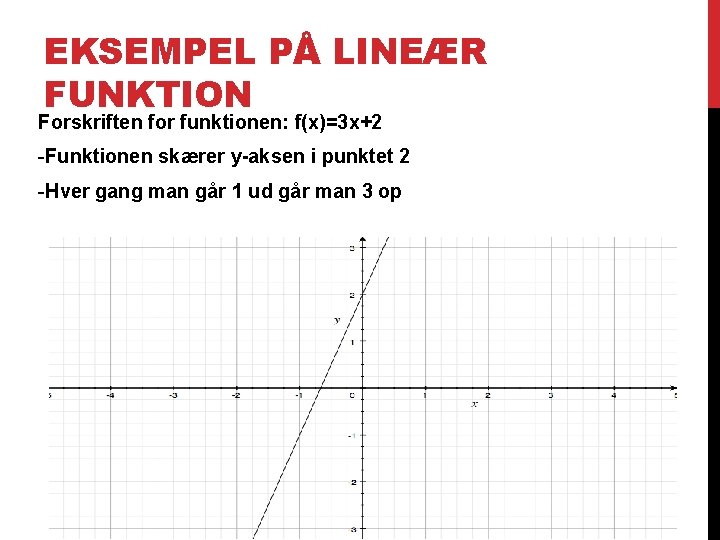
EKSEMPEL PÅ LINEÆR FUNKTION Forskriften for funktionen: f(x)=3 x+2 -Funktionen skærer y-aksen i punktet 2 -Hver gang man går 1 ud går man 3 op

FORMEL 19 Formlen hedder: Formlen bruges til at finde hældningen (a) i en lineær funktion a=hældningen på grafen y = y 2 -y 1 x = x 2 -x 1 Formlen kan udledes via geometrisk metode som:

y 1 = ax 1+b ^ y 2 = ax 2+b y 1 - ax 1 1) =b ^ y 2 = ax 2+b y 1 - ax 1 =b ^ y 2 = ax 2+(y 1 -ax 1)2) y 1 - ax 1 =b ^ y 2 = ax 2+y 1 -ax 1 3) y 1 - ax 1 =b ^ y 2 -y 1 = ax 2 -ax 1 4) y 1 - ax 1 =b ^ y 2 -y 1 = a(x 2 -x 1) 5) y 1 - ax 1 =b ^ 6) = BEVIS FORMEL 19

FORMEL 22 Formlen hedder: b=y-ax Formlen bruges til at finde skæringen med y-aksen (b) b=skæringen med y-aksen y= y 1 eller y 2 ax= a * med den tilhørende x-værdi til den valgte y-værdi

SKÆRING AF TO LINJER Der er to metoder man kan benytte, når man skal finde skæringen mellem to linjer 1. Aflæsning på koordinatsystem 2. Stille de 2 funktioner over for hinanden ligesom en ligning (når x er fundet, sættes x ind i funktionerne og derefter findes y)

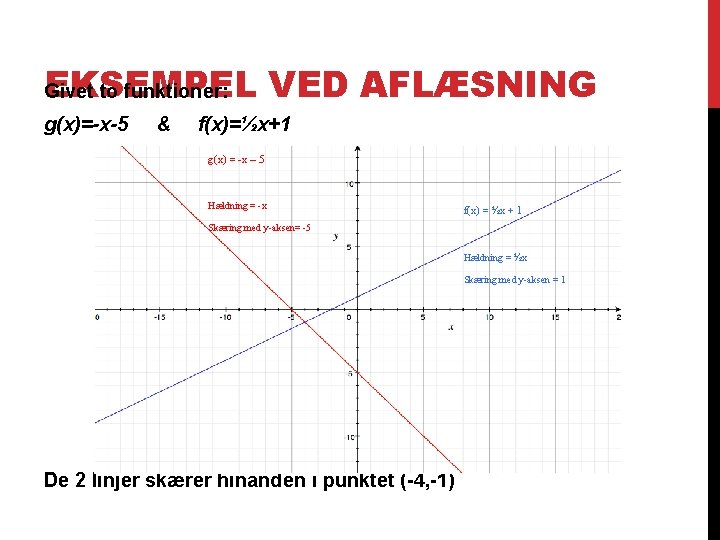
EKSEMPEL VED AFLÆSNING Givet to funktioner: g(x)=-x-5 & f(x)=½x+1 g(x) = -x – 5 Hældning = -x f(x) = ½x + 1 Skæring med y-aksen= -5 Hældning = ½x Skæring med y-aksen = 1 De 2 linjer skærer hinanden i punktet (-4, -1)

EKSEMPEL VED BEREGNING Beregning af x 0, 5 x+1=-x-5 Beregning af y f(x)=0, 5 x+1 1, 5 x=-6 y=-2+1 x=-4 y=-1 g(x)=-x-5 y=4 -5 y=-1 Funktionen skærer hinanden i punktet (-4, -1)

LIGNINGER Ligninger kan løses ved hjælp af 2 metoder: 1. Man kan omforme ligningen, således at x står på den ene side og talværdierne på den anden side af lighedstegnet 2. Man kan gætte og kontrollere ved at indsætte et tal i stedet for x

NÅR EN LIGNING OMFORMES Man skal lægge/trække samme tal til på begge sider af lighedstegnet. Man skal gange/dividere med samme tal på begge sider af lighedstegnet Alle ligninger kræver grundmængde, ensbetydendetegn og løsningsmængde Der indgår aldrig x i løsningsmængden Hvis man vil sikre sig at ligningen er rigtig, kan der foretages en kontrol (Det fundne x sættes ind på x’s plads)

EKSEMPEL PÅ EN LIGNING G=R 6(x-2)=2 x+16 Ligningen er skrevet op 6 x-12=2 x+16 Parantesen løses 4 x=28 x’erne står på samme side x=7 L={7} løsningen er fundet løsningen er skrevet op

ULIGHEDER Man skal lægge/trække samme tal til på begge sider af ulighedstegnet Man skal gange/dividere med samme positive tal på begge sider af ulighedstegnet Man må gange og dividere med samme negative tal på begge sider af ulighedstegnet, hvis man samtidig vender ulighedstegnet Alle uligheder kræver grundmængde, ensbetydendetegn og løsningsmængde Hvis der ingen løsning er, skrives løsningen som L=Ø

EKSEMPEL PÅ ULIGHED Uligheden: 2 x - 8 < -3 x + 2 G= R 2 x - 8 < -3 x + 2 2 x+3 x < 2 + 8 5 x < x L = ]- ; 2[ 10 < 2

DOBBELTULIGHED Samme regler gælder ved en dobbeltulighed -Som en hjælp kan man opstille en linje, hvor talstørrelserne sættes ind -Det der er imellem talstørrelserne indgår i løsningen

EKSEMPEL PÅ DOBBELTULIGHED Dobbeltuligheden: 4 x - 6 < 2 x + 2 < 6 x + 14 G = R*R 4 x - 6 < 2 x + 2 < 6 x + 14 4 x - 6 < 2 x + 2 ^ 2 x + 2 < 6 x + 14 2 x < 8 ^ x < 4 ^ x > 3 L = ]3; 4] -4 x < 12

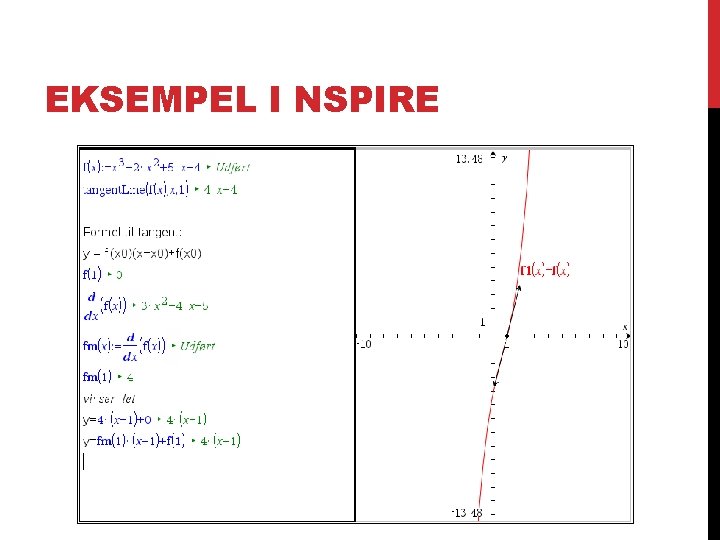
TANGENTBESTEMMELSE Funktionen f har forskriften: f(x) = 2 x 2 – 5 x , som har en tangent i punktet (2; f(2)). Man skal differentier funktionen, som kommer til at hedde: f’(x)=4 x-5 Tangentformlen til at finde en tangents hældning er: Nu sættes 2 ind på x-plads i den differentieret funktion og den oprindelige funktion f’(2)=4(2)-5=3 f(2)=2*(2)^2 -5(2)=-2

TANGENTBESTEMMEL SE FORTSAT Nu benyttes tangentformlen f(x)=3(x-2)+(-2) f(x)=3 x-6 -2 f(x)=3 x-8 Tangentshældning kommer derfor til at hedde f(x)=3 x-8

EKSEMPEL I NSPIRE
 Tangentbestemmelse
Tangentbestemmelse Vel kan vi strides om guder og
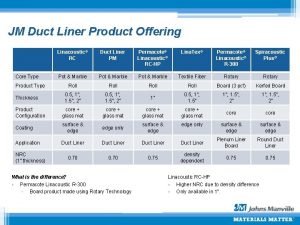
Vel kan vi strides om guder og Polyurea geotextile liner
Polyurea geotextile liner Cylinder liner definition
Cylinder liner definition Calendering process
Calendering process Linacoustic
Linacoustic Texel pond liner
Texel pond liner Non-linear plot
Non-linear plot Tramp liner
Tramp liner Soft liner composition
Soft liner composition An example of an enamel bonding procedure is
An example of an enamel bonding procedure is Gmaw power supplies are
Gmaw power supplies are Controller
Controller Hdpe liner
Hdpe liner Cavity liners and bases
Cavity liners and bases Variabel adalah
Variabel adalah Bases in dentistry
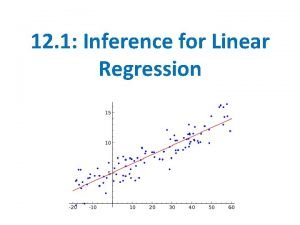
Bases in dentistry Conditions for inference regression
Conditions for inference regression Frac pond liner
Frac pond liner Frac pit liners
Frac pit liners Pertidaksamaan nilai mutlak
Pertidaksamaan nilai mutlak