Liner algebra Innledning Liner algebra er sentral i

Lineær algebra Innledning Lineær algebra er sentral i: … Likningsløsninger Representasjon av multidimensjonale datamateriell Representasjon innen geometri Representasjon i computere GPS med korteste vei-beregninger Modellering

Lineær algebra Matriser er todimensjonale tabeller bestående av m rader og n kolonner og inneholdende reelle og/eller komplekse tall Eks: En 3 x 4 matrise (3 rader og 4 kolonner) inneholdende naturlige tall

Lineær algebra Addisjon av matriser utføres cellevis og krever at begge matrisene har samme dimensjon. Eks:

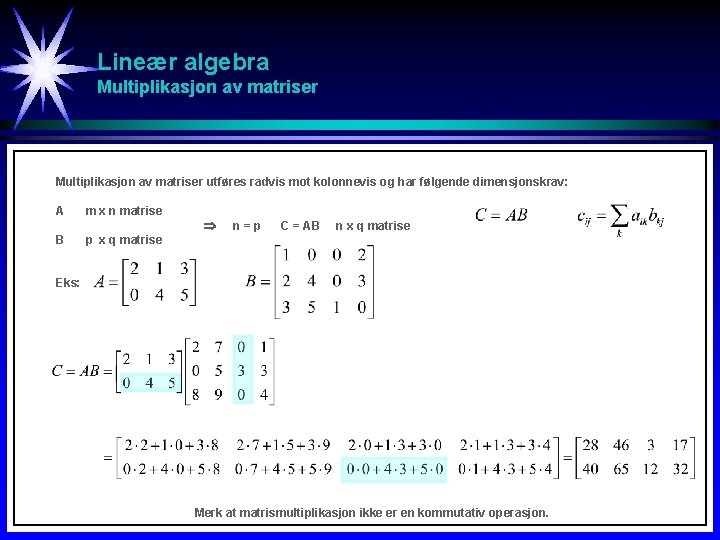
Lineær algebra Multiplikasjon av matriser utføres radvis mot kolonnevis og har følgende dimensjonskrav: A B m x n matrise n=p C = AB n x q matrise p x q matrise Eks: Merk at matrismultiplikasjon ikke er en kommutativ operasjon.

Lineær algebra Transponert av en matrise Den transponerte matrisen AT av en matrise A fremkommer ved å bytte rader og kolonner.

Lineær algebra Determinanter 2 x 2 matrise 3 x 3 matrise

Lineær algebra Likningsløsning - 2 likninger med 2 ukjente

Lineær algebra Likningsløsning - 3 likninger med 3 ukjente

Lineær algebra Invers av en matrise Med en invers matrise A-1 (hvis den finnes) til en gitt matrise A mener vi en matrise A-1 som multiplisert med matrisen A (både fra venstre og høyre) gir identitsmatrisen. Kun kvadratiske matriser kan ha en invers matrise. Eksistens av invers matrise A-1 er ekvivalent med at det(A) 0. Identitetsmatrisen er entydig.

Lineær algebra Invers av en matrise 2 x 2

Lineær algebra Invers av en matrise 3 x 3

Lineær algebra Likningsløsning vha invers matrise: En ortogonal matrise er definert ved følgende egenskap: For ortogonale matriser er den transponerte lik den inverse

Lineær algebra Matriser for translasjon og rotasjon i planet

END