Linearization of Stream Ciphers in Terms of Cellular

Linearization of Stream Ciphers in Terms of Cellular Automata Amparo Fúster-Sabater Institute of Applied Physics (CSIC) Madrid (Spain) amparo@iec. csic. es A. Fúster-Sabater Gjøvik University College June 2006

Overview Introduction n Basic structures n LFSR-Based Keystream Generators n Cellular Automata (CA) n Linear model of a class of Keystream Generators n Contributions to Cryptanalysis n Conclusions n A. Fúster-Sabater Gjøvik University College June 2006

“Linearity is the curse of the cryptographer” - James L. Massey Crypto’ 89 A. Fúster-Sabater Gjøvik University College June 2006

Stream Cipher Procedure • sender 001… 10 011… 01 010… 11 000… 10 110… 01 010… 11 010… 01 100… 10 010… 11 011… 01 010… 01 000… 10 100… 10 010… 11 001… 10 010… 11 …. . (plain text) (keystream seq. ) …. . (ciphered text) (keystream seq. ) (ciphered text) • receiver n (plain text) Stream cipher: design of keystream sequence generators with pseudorandomness characteristics A. Fúster-Sabater Gjøvik University College June 2006

Linear Feedback Shift Register (LFSR) 1 0 0 0 n n n LFSR’s Parameters: 0 0 0 1 n Length L 0 0 1 1 n Characteristic polynomial 0 1 1 1 1 They work: n Shifting of the binary content 1 1 1 0 n Feedback bit entrance 1 1 0 1 Generated sequence: 1 0 0 0 1 1 …… A. Fúster-Sabater Gjøvik University College 1 0 June 2006

Linear Feedback Shift Registers n LFSRs generate PN-sequences: n n Long period Good statistics Low linear complexity Cryptographic applications: Non-linear combinations of LFSRs n n n Non-linear filters Non-linear combining generators Clock-controlled generators A. Fúster-Sabater Gjøvik University College June 2006

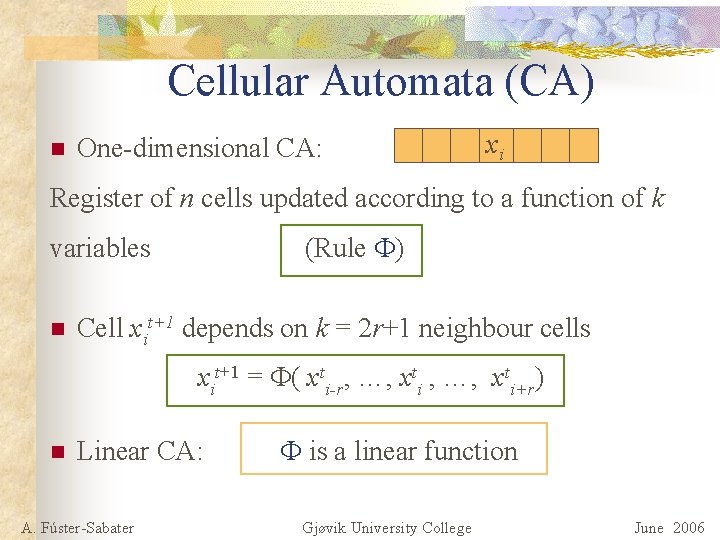
Cellular Automata (CA) n One-dimensional CA: xi Register of n cells updated according to a function of k (Rule ) variables n Cell xit+1 depends on k = 2 r+1 neighbour cells xit+1 = ( xti-r, …, xti+r) n Linear CA: A. Fúster-Sabater is a linear function Gjøvik University College June 2006

Classification of CA v Uniform or Regular CA All the cells follow the same rule v Hybrid CA Different cells follow different rules i n Null boundary conditions Cells adjacent to the extreme cells are supposed with permanent null content n Periodic boundary conditions Extreme cells are supposed adjacent A. Fúster-Sabater Gjøvik University College xi June 2006

Linear Cellular Automata n k =3 n Rule 90 xit+1 = xti-1 xti+1 110 101 100 011 010 001 000 0 1 1 0 01011010 (binary) = 90 (decimal) n Rule 150 xit+1 = xti-1 xti+1 110 101 100 011 010 001 000 1 0 10010110 (binary) = 150 (decimal) A. Fúster-Sabater Gjøvik University College June 2006

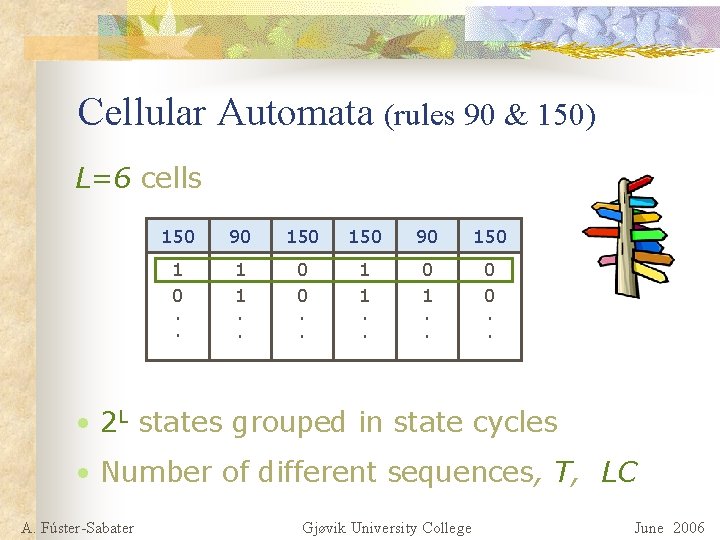
Cellular Automata (rules 90 & 150) L=6 cells 150 90 150 1 0. . 1 1. . 0 0. . • 2 L states grouped in state cycles • Number of different sequences, T, LC A. Fúster-Sabater Gjøvik University College June 2006

References 1. 2. 3. 4. 5. 6. 7. A. Fúster-Sabater S. Wolfram, Cellular Automata as Models of Complexity, Nature, Vol. 311, pp. 419, 1984. S. Wolfram, Random Sequence Generation by Cellular Automata , Avd. Appl. Math. , Vol. 7, pp. 127 – 169, 1986. S. Zhang et al. Quantitative Analysis for Cellular Automata and LFSR as BIST Generators, J. Electro. Testing, 7 (3), 1995. M. Serra et al. Analysis of One-dimensional CA and their Aliasing Properties, IEEE Trans. Comp. Aided Design, 9 (2), 1990. A. K. Das et al. Efficient Characterization of Cellular Automata , IEE Proc. Part E. 1, pp. 81 -87, 1990. S. J. Cho et al. Computing Phase Shifts of 90/150 CA Sequences. Proc. ACRI 2004, LNCS, 3305, pp. 31 – 39, 2004. A. Fúster et al. Concatenated Automata in Stream Ciphers. To appear in Proc. ACRI 2006, LNCS, 2006. Gjøvik University College June 2006

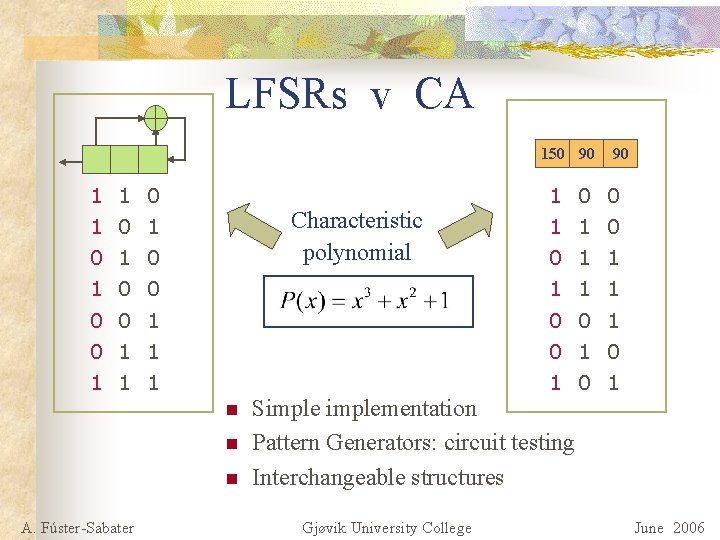
LFSRs v CA 150 90 1 1 0 90 1 0 0 Characteristic polynomial 1 0 1 0 1 1 0 0 1 0 1 0 1 n n n A. Fúster-Sabater Simplementation Pattern Generators: circuit testing Interchangeable structures Gjøvik University College June 2006

More References n CA n n Characteristic Polynomial S. Zhang et al. , Quantitative Analysis for Linear Hybrid Cellular Automata and LFSR as Built-In Self-Test Generators for Sequential Faults, J. of Electronic Testing: Theory and Applications, 7 (1995), 209 – 221. Characteristic Polynomial n A. Fúster-Sabater CA K. Cattel and J. C. Muzio, The Synthesis of One. Dimensional Linear Hybrid Cellular Automata, IEEE Trans. On Computer-Aided Design. 15 (1996) 325 -335. Gjøvik University College June 2006

A Class of LFSR-Based Generators: Clock-Controlled Shrinking Generators n n A wide class of binary sequence generators Made up of two LFSRs: R 1 and R 2 n n R 1 (Selector register) clocked normally R 2 (Generating register) clocked irregularly According to a rule P, the bits of register R 1 control the clock of register R 2 n This construction allows users to generate a large family of different sequences using the same registers and initial. Gjøvik states but. College changing the rule P A. Fúster-Sabater University June 2006 n

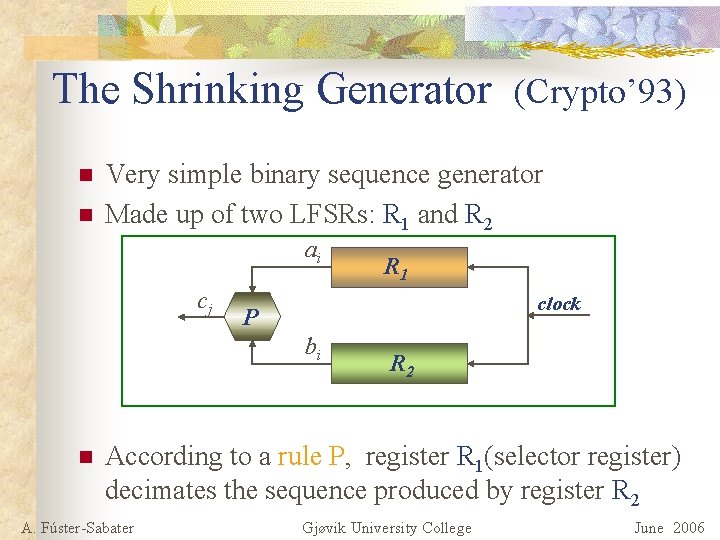
The Shrinking Generator (Crypto’ 93) n n Very simple binary sequence generator Made up of two LFSRs: R 1 and R 2 ai cj clock P bi n R 1 R 2 According to a rule P, register R 1(selector register) decimates the sequence produced by register R 2 A. Fúster-Sabater Gjøvik University College June 2006

The Shrinking Generator n {ai} binary sequence generated by R 1 {bi} binary sequence generated by R 2 n {cj} output sequence of the SG: n “the shrunken sequence” n Decimation rule P: 1. If ai = 1 cj = bi 2. If ai = 0 bi is discarded A. Fúster-Sabater Gjøvik University College June 2006

The Shrinking Generator: Example LFSRs: 1. R 1 : 2. R 2 : Decimation rule P: n n n {ai}= 1 0 0 1 1 1 0 1 0 … {bi}= 1 0 0 0 1 1 … {cj}= 1 0 1 1 … The underlined bits 1 and 0 are discarded A. Fúster-Sabater Gjøvik University College June 2006

Cryptographic characteristics of the shrunken sequence n Period: n Linear Complexity: n Number of 1’s: quasi-balanced sequence A. Fúster-Sabater Gjøvik University College June 2006

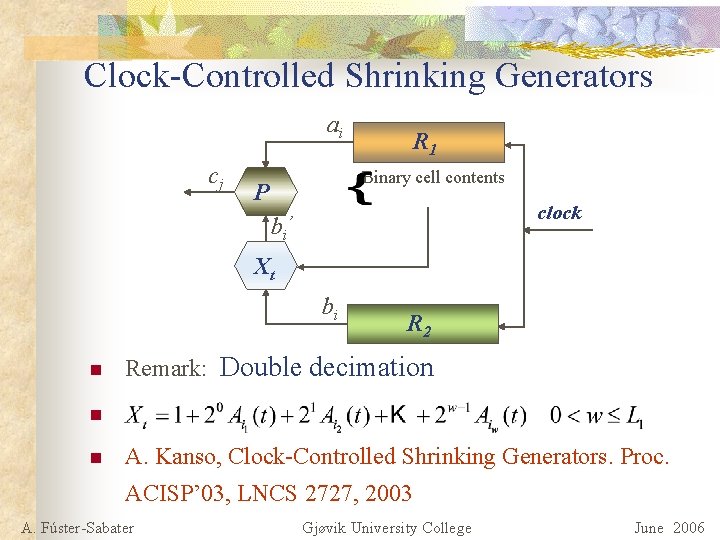
Clock-Controlled Shrinking Generators ai cj R 1 Binary cell contents P clock bi’ Xt bi n R 2 Remark: Double decimation n n A. Kanso, Clock-Controlled Shrinking Generators. Proc. ACISP’ 03, LNCS 2727, 2003 A. Fúster-Sabater Gjøvik University College June 2006

CCSG: An Example For the same LFSRs as before and R 1 P X R 2 Decimation rule X: (if Xt =1 => the shrinking generator) n n n {bi}= 1 0 0 0 1 1 0 0 0 1… {X}= 2 1 1 2 2 2 1 2 1 1 2 2… {bi’}= 1 0 0 1 1 1 0 1 0 1 1… Decimation rule P: n n n {ai}= 1 0 0 1 1 1 0 1 0 … {bi’}= 1 0 0 1 1 1 0 1 0 … {cj}= 1 1 0 1 0 1 1 … A. Fúster-Sabater Gjøvik University College June 2006

CCSG in terms of CA n Given A Clock-Controlled Shrinking Generator characterized by its LFSRs n expressing it in terms of Null Hybrid Linear Cellular Automata with rules 90 and 150 A. Fúster-Sabater Gjøvik University College June 2006

Fact 1: n The characteristic polynomial of the shrunken sequence is of the form: n P(x) is an L 2 - degree primitive polynomial n N satisfies A. Fúster-Sabater Gjøvik University College June 2006

R 1 Fact 2: P R 2 P(x) depends exclusively on: 1. 2. n The characteristic polynomial P 2(x) of the register R 2 The length L 1 of the register R 1 Different SG will have the same characteristic polynomial. A. Fúster-Sabater Gjøvik University College June 2006

Algorithm of Linearization n Input: A Shrinking Generator (given L 1 , L 2 , P 2(x)) n Output: Two linear CA corresponding to the given SG A. Fúster-Sabater Gjøvik University College June 2006

Step 1: Computation of P(x) n P(x) is obtained from L 1 and P 2(x) n P(x) is the characteristic polynomial of the cyclotomic Coset E n being a primitive root in A. Fúster-Sabater Gjøvik University College June 2006

Step 2: Computation of the CA corresponding to P(x) n Apply to P(x) the “Cattel and Muzio synthesis algorithm” to determine the two linear hybrid CA of length L 2 whose characteristic polynomials are P(x) n Codify both CA according to: rule 90 = 0 and rule 150 = 1 A. Fúster-Sabater Gjøvik University College June 2006

Step 3: Computation of the CA corresponding to the given SG For each obtained CA: 1. Complement its least significant bit S 2. Compute its mirror image S* and concatenate both strings n Iterate 1. and 2. (L 1 -1) times A. Fúster-Sabater Gjøvik University College June 2006

Algorithm (An Example) n Shrinking Generator: R 1 n R 2 n (not needed) Step 1 n A. Fúster-Sabater is the characteristic polynomial of Coset 7 Gjøvik University College June 2006

Algorithm (An Example) Step 2 n Determine two linear CA corresponding to via Cattel and Muzio algorithm n Both CA are codified: (0 = ley 90, 1 = ley 150) 011110 A. Fúster-Sabater Gjøvik University College June 2006

Algorithm (Step 3) n First automata: 01111 0111001111001110 n L 1 -1 times Second automata: 11110 111110011111 A. Fúster-Sabater Gjøvik University College L 1 -1 times June 2006

Linearization Algorithm for CCSGs n CCSG: given R 1 n R 2 n Xt n (not needed) n In Step 1, Coset E n The other steps of the algorithm are as before CCSGs can be expressed in terms of linear CA too n A. Fúster-Sabater is the characteristic polynomial of Gjøvik University College June 2006

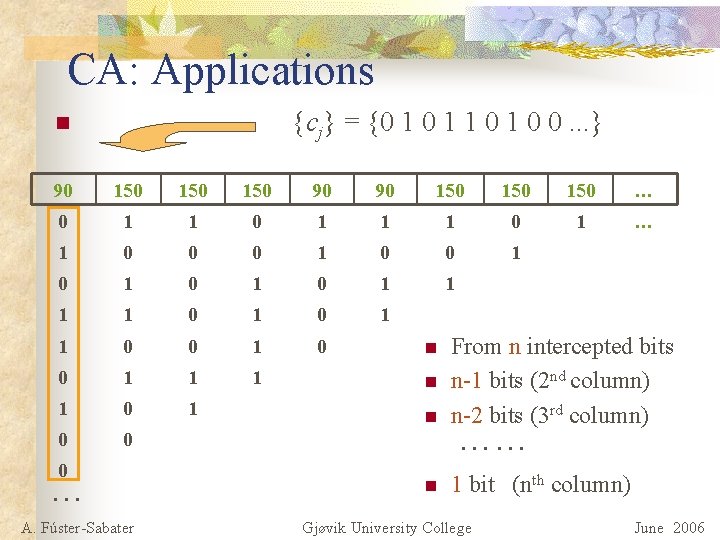
CA: Applications {cj} = {0 1 1 0 0. . . } n 90 150 150 90 90 150 150 … 0 1 1 1 0 1 … 1 0 0 0 1 0 1 0 1 1 0 0 1 1 0 1 0 0 0 … A. Fúster-Sabater n From n intercepted bits n-1 bits (2 nd column) n-2 bits (3 rd column) n 1 bit (nth column) n n …… Gjøvik University College June 2006

Reconstruction of the shrunken sequence n From n intercepted bits of the shrunken sequence n IDEA: use these bits to determine portions of the shrunken sequence A. Fúster-Sabater Gjøvik University College June 2006

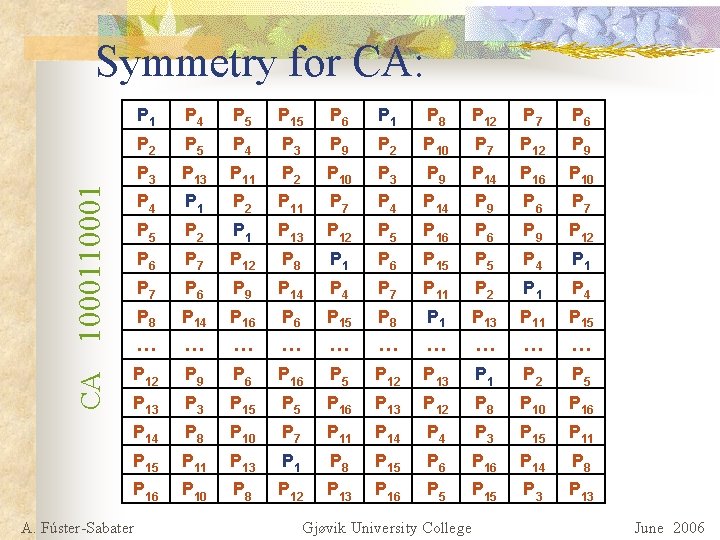
Symmetry for CA: P 4 P 5 P 15 P 6 P 1 P 8 P 12 P 7 P 6 P 2 P 5 P 4 P 3 P 9 P 2 P 10 P 7 P 12 P 9 P 3 P 11 P 2 P 10 P 3 P 9 P 14 P 16 P 10 P 4 P 1 P 2 P 11 P 7 P 4 P 14 P 9 P 6 P 7 P 5 P 2 P 13 P 12 P 5 P 16 P 9 P 12 P 6 P 7 P 12 P 8 P 1 P 6 P 15 P 4 P 1 P 7 P 6 P 9 P 14 P 7 P 11 P 2 P 1 P 4 P 8 P 14 P 16 P 15 P 8 P 13 P 11 P 15 … … … … … P 12 P 9 P 6 P 16 P 5 P 12 P 13 P 1 P 2 P 5 P 13 P 15 P 16 P 13 P 12 P 8 P 10 P 16 P 14 P 8 P 10 P 7 P 11 P 14 P 3 P 15 P 11 P 13 P 1 P 8 P 15 P 6 P 14 P 8 P 16 P 10 P 8 P 12 P 13 P 16 P 5 P 15 P 3 P 13 CA 10001 P 1 A. Fúster-Sabater Gjøvik University College June 2006

Other sequences generated by CA n Different shrinking generators The same R 2 n Different R 1 with length L 1 n n LFSR-based generators Different rules of decimation n Clock-controlled shrinking generators n A. Fúster-Sabater Gjøvik University College June 2006

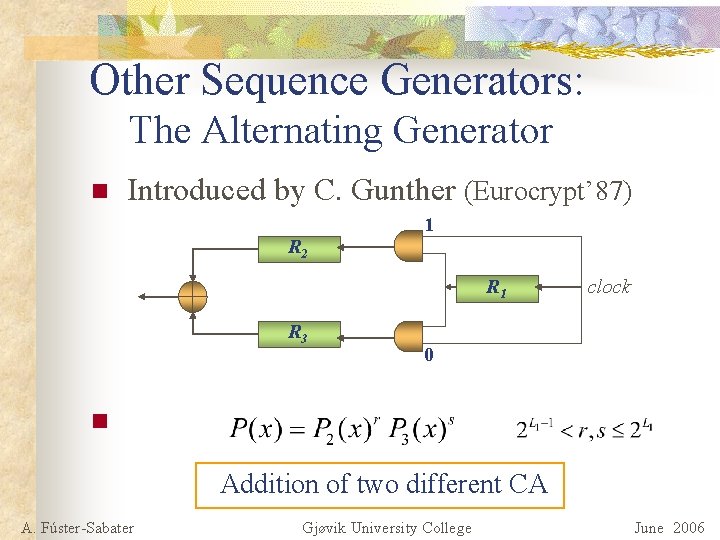
Other Sequence Generators: The Alternating Generator n Introduced by C. Gunther (Eurocrypt’ 87) 1 R 2 R 1 R 3 clock 0 n Addition of two different CA A. Fúster-Sabater Gjøvik University College June 2006

Other Sequence Generators: The Gollmann Generator n Introduced by D. Gollmann (IEE Proc. 1988) 1 R 2 R 3 clock n Addition of two (or more) CA A. Fúster-Sabater Gjøvik University College June 2006

Conclusions LFSR-based structures Cellular Automata Classes of CC Generators are a Subset of Linear Cellular Automata Linear Models describe the behavior of the CC Sequence Generators A. Fúster-Sabater Gjøvik University College June 2006

Conclusions n Very simple algorithm to convert different classes of CC generators into linear CA-based model n A wide class of non-linear binary generators can be expressed as linear models (by concatenation) n A wide class of different binary generators are included in the same cellular automata n The algorithm can be applied to CC generators in a range of cryptographic interest A. Fúster-Sabater Gjøvik University College June 2006

For the Future n Apply the same technique of linearization to other nonlinear LFSR-based keystream generators A. Fúster-Sabater Gjøvik University College June 2006