Linear Transformations 3 1 Introduction to Linear Transformations














































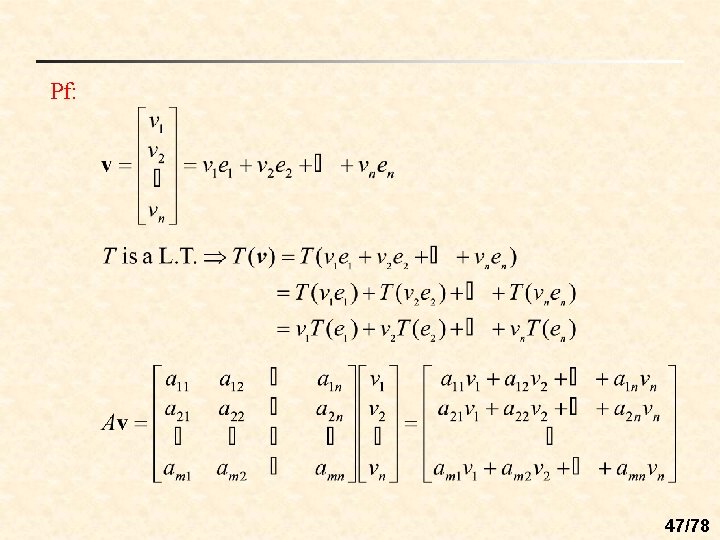


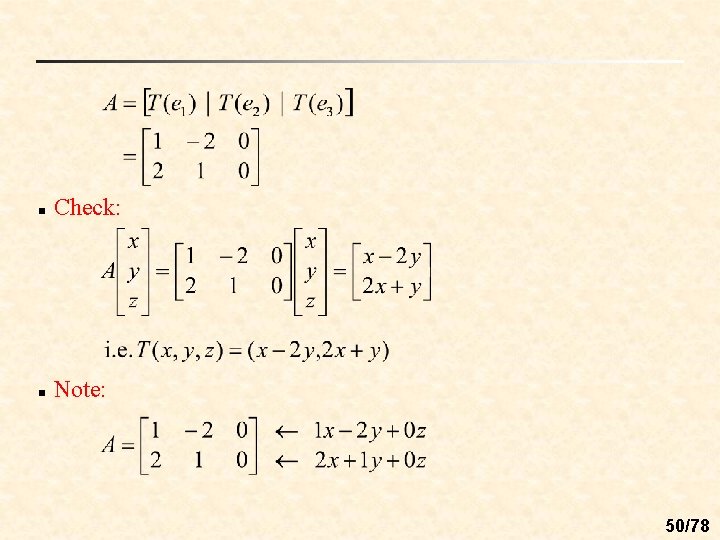


- Slides: 53

Linear Transformations 3. 1 Introduction to Linear Transformations 3. 2 The Kernel and Range of a Linear Transformation 3. 3 Matrices for Linear Transformations 3. 4 Transition Matrices and Similarity

3. 1 Introduction to Linear Transformations n Function T that maps a vector space V into a vector space W: V: the domain of T W: the codomain of T 1/78

n Image of v under T: If v is in V and w is in W such that Then w is called the image of v under T. n n the range of T: The set of all images of vectors in V. the preimage of w: The set of all v in V such that T(v)=w. 2/78

n Ex : (A function from R 2 into R 2 ) (a) Find the image of v=(-1, 2). (b) Find the preimage of w=(-1, 11) Sol: Thus {(3, 4)} is the preimage of w=(-1, 11). 3/78

n Linear Transformation (L. T. ): 4/78

n Notes: (1) A linear transformation is said to be operation preserving. Addition in V Addition in W Scalar multiplication in V (2) A linear transformation itself is called a linear operator. Scalar multiplication in W from a vector space into 5/78

n Ex : (Verifying a linear transformation T from R 2 into R 2) Pf: 6/78

Therefore, T is a linear transformation. 7/78

n Ex : (Functions that are not linear transformations) 8/78

n Notes: Two uses of the term “linear”. (1) is called a linear function because its graph is a line. (2) is not a linear transformation from a vector space R into R because it preserves neither vector addition nor scalar multiplication. 9/78

n Zero transformation: n Identity transformation: n Th : (Properties of linear transformations) 10/78

n Ex : (Linear transformations and bases) Let be a linear transformation such that Find T(2, 3, -2). Sol: (T is a L. T. ) 11/78

n Ex : (A linear transformation defined by a matrix) The function is defined as Sol: (vector addition) (scalar multiplication) 12/78

n Th : (The linear transformation given by a matrix) Let A be an m n matrix. The function T defined by is a linear transformation from Rn into Rm. n Note: 13/78

n Ex : (Rotation in the plane) Show that the L. T. given by the matrix has the property that it rotates every vector in R 2 counterclockwise about the origin through the angle . Sol: (polar coordinates) r: the length of v :the angle from the positive x-axis counterclockwise to the vector v 14/78

r:the length of T(v) + :the angle from the positive x-axis counterclockwise to the vector T(v) Thus, T(v) is the vector that results from rotating the vector v counterclockwise through the angle . 15/78

n Ex : (A projection in R 3) The linear transformation is given by is called a projection in R 3. 16/78

n Ex : (A linear transformation from Mm n into Mn m ) Show that T is a linear transformation. Sol: Therefore, T is a linear transformation from Mm n into Mn m. 17/78

Keywords in Section 3. 1: n function n domain n codomain n image of v under T n range of T n preimage of w n linear transformation n linear operator n zero transformation n identity transformation 18/78

3. 2 The Kernel and Range of a Linear Transformation n Kernel of a linear transformation T: Let be a linear transformation Then the set of all vectors v in V that satisfy called the kernel of T and is denoted by ker(T). n is Ex : (Finding the kernel of a linear transformation) Sol: 19/78

n Ex : (The kernel of the zero and identity transformations) (a) T(v)=0 (the zero transformation ) (b) T(v)=v (the identity transformation n ) Ex : (Finding the kernel of a linear transformation) Sol: 20/78

n Ex : (Finding the kernel of a linear transformation) Sol: 21/78

22/78

n Th : (The kernel is a subspace of V) The kernel of a linear transformation is a subspace of the domain V. Pf: n Note: The kernel of T is sometimes called the nullspace of T. 23/78

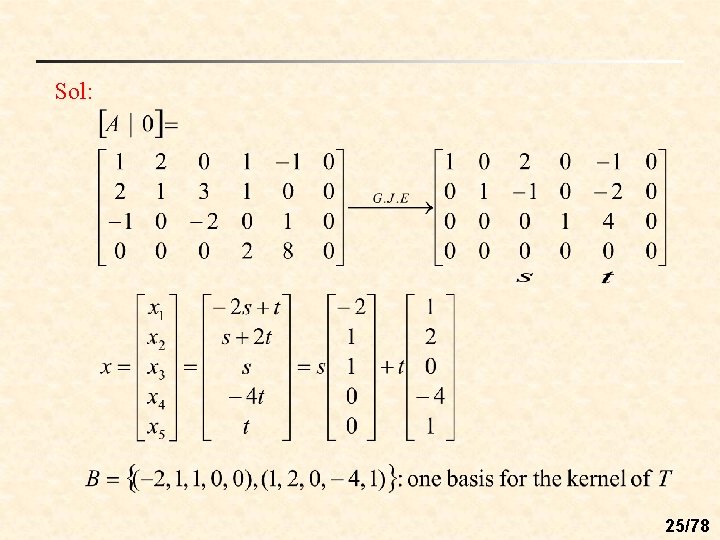
n Ex : (Finding a basis for the kernel) Find a basis for ker(T) as a subspace of R 5. 24/78

Sol: 25/78

n Corollary : n Range of a linear transformation T: 26/78

n Th : (The range of T is a subspace of W) Pf: 27/78

n Notes: n Corollary : 28/78

n Ex : (Finding a basis for the range of a linear transformation) Find a basis for the range of T. 29/78

Sol: 30/78

n Rank of a linear transformation T: V→W: n Nullity of a linear transformation T: V→W: n Note: 31/78

n Thm 6. 5: (Sum of rank and nullity) 32/78

n Ex : (Finding the rank and nullity of a linear transformation) Sol: 33/78

n Ex : (Finding the rank and nullity of a linear transformation) Sol: 34/78

n One-to-one: one-to-one not one-to-one 35/78

n Onto: (T is onto W when W is equal to the range of T. ) 36/78

n Thm : (One-to-one linear transformation) Pf: 37/78

n Ex : (One-to-one and not one-to-one linear transformation) 38/78

n Th : (Onto linear transformation) n Th : (One-to-one and onto linear transformation) Pf: 39/78

n Ex : Sol: T: Rn→Rm dim(domain of T) rank(T) nullity(T) 1 -1 onto (a)T: R 3→R 3 3 3 0 Yes (b)T: R 2→R 3 2 2 0 Yes No (c)T: R 3→R 2 3 2 1 No Yes (d)T: R 3→R 3 3 2 1 No No 40/78

n n Isomorphism: Th : (Isomorphic spaces and dimension) Two finite-dimensional vector space V and W are isomorphic Pf: if and only if they are of the same dimension. 41/78

It can be shown that this L. T. is both 1 -1 and onto. Thus V and W are isomorphic. 42/78

n Ex : (Isomorphic vector spaces) The following vector spaces are isomorphic to each other. 43/78

Keywords in Section 3. 2: n kernel of a linear transformation T n range of a linear transformation T n rank of a linear transformation T n nullity of a linear transformation T n one-to-one n onto n isomorphism(one-to-one and onto) n isomorphic space 44/78

3. 3 Matrices for Linear Transformations n Two representations of the linear transformation T: R 3→R 3 : n Three reasons for matrix representation of a linear transformation: n It is simpler to write. n It is simpler to read. n It is more easily adapted for computer use. 45/78

n Th : (Standard matrix for a linear transformation) 46/78
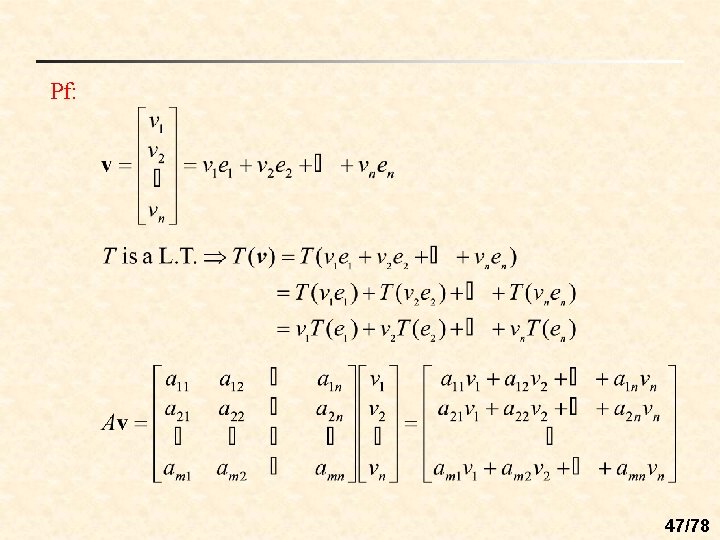
Pf: 47/78

48/78

n Ex 1: (Finding the standard matrix of a linear transformation) Sol: Vector Notation Matrix Notation 49/78
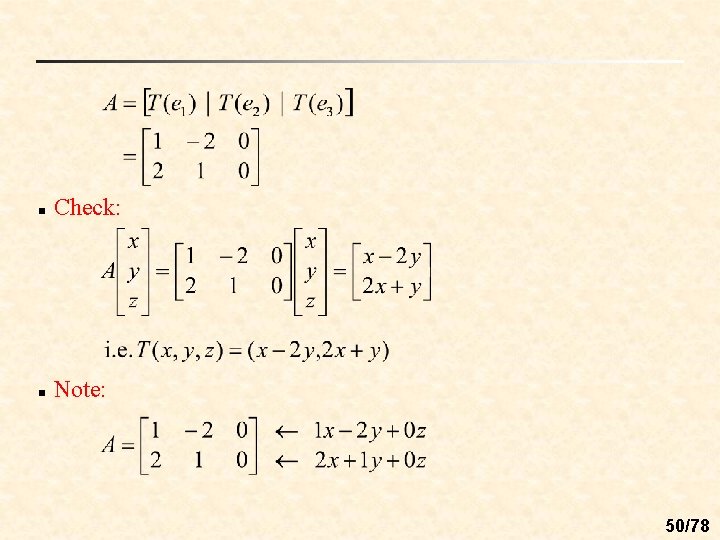
n Check: n Note: 50/78

n Ex 2: (Finding the standard matrix of a linear transformation) Sol: n Notes: (1) The standard matrix for the zero transformation from Rn into Rm is the m n zero matrix. (2) The standard matrix for the zero transformation from Rn into Rn is the n n identity matrix In 51/78

Keywords in Section 3. 3: n standard matrix for T 52/78