Linear Time Graph Partitioning via Fast Simulation of

Linear Time Graph Partitioning via Fast Simulation of Random walks Institute for Advanced Study, April 16 2012 Sushant Sachdeva Princeton University Joint work with Lorenzo Orecchia, Nisheeth K. Vishnoi

Theory of near-linear time algorithms INTRODUCTION

Why linear-time algorithms? Input graphs and data sets are massive. e. g. Web graph (1011 nodes), Social networks (109 nodes) Super-linear algorithms are impractical. Need time algorithms for fundamental problems: e. g. MAX-MATCHING, s-t MINCUT/MAXFLOW, Balanced Graph Partitioning (1 -²) approx. , time (1 -²) approx. , Spectral approx. , time [Duan and Pettie] [This talk] [Christiano et al. ] time Approximate solutions maybe? © 2004– 2012 Michael K. Bergman.

GRAPH PARTITIONING

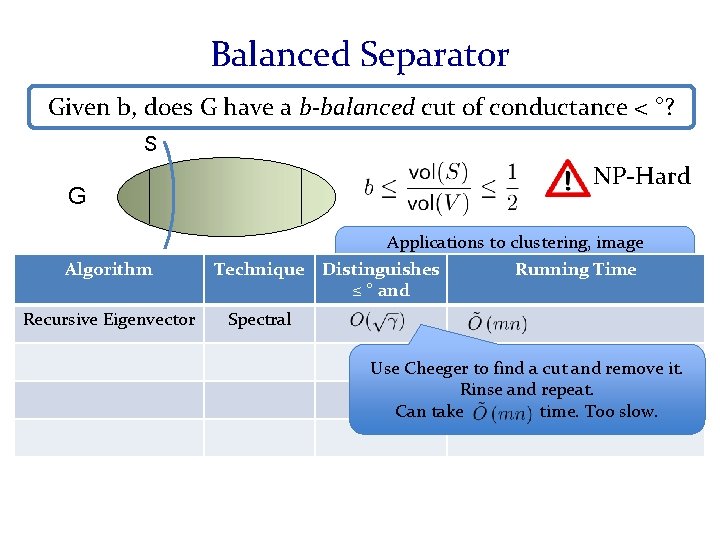
Conductance Given a undirected, unweighted graph Conductance of S Conductance of G [Spielman-Teng] allows us to approximate ¸ 2(L) and find such a cut in time Fundamental quantity in Markov [Cheeger, Alon-Milman] Chains, Riemannian Manifolds Spectral approximation Assume G is d-regular

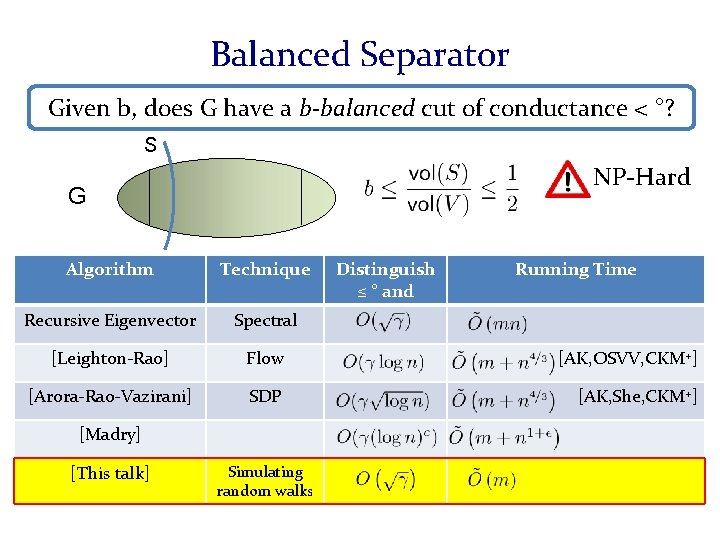
Balanced Separator Given b, does G have a b-balanced cut of conductance < °? S NP-Hard G Algorithm Recursive Eigenvector Applications to clustering, image segmentation, community Technique Distinguishes Runningdetection, Time primitive for divide-and-conquer ≤ ° and Spectral Use Cheeger to find a cut and remove it. Rinse and repeat. Can take time. Too slow.

Balanced Separator Given b, does G have a b-balanced cut of conductance < °? S NP-Hard G Algorithm Technique Distinguishes ≤ ° and Running Time Recursive Eigenvector Spectral [Leighton-Rao] Flow [AK, OSVV, CKM+] [Arora-Rao-Vazirani] SDP [AK, She, CKM+] [Madry]

Balanced Separator Given b, does G have a b-balanced cut of conductance < °? S NP-Hard G Algorithm Technique Recursive Eigenvector Spectral [Spielman-Teng] Local Random walks [Andersen-Peres] Evolving Sets [Orecchia-Vishnoi] SDP Distinguishes ≤ ° and Running Time

Balanced Separator Given b, does G have a b-balanced cut of conductance < °? S NP-Hard G Algorithm Technique Recursive Eigenvector Spectral [Spielman-Teng] Local Random walks [Andersen-Peres] Evolving Sets [Orecchia-Vishnoi] SDP [This talk] Simulating Random walks Distinguishes ≤ ° and Running Time

Balanced Separator Given b, does G have a b-balanced cut of conductance < °? S NP-Hard G Algorithm Technique Recursive Eigenvector Spectral [Leighton-Rao] Flow [AK, OSVV, CKM+] [Arora-Rao-Vazirani] SDP [AK, She, CKM+] [Madry] [This talk] Simulating random walks Distinguish ≤ ° and Running Time

Overview 1. Use continuous-time random walks to give an algorithm 2. Show to simulate continuous-time random walks fast

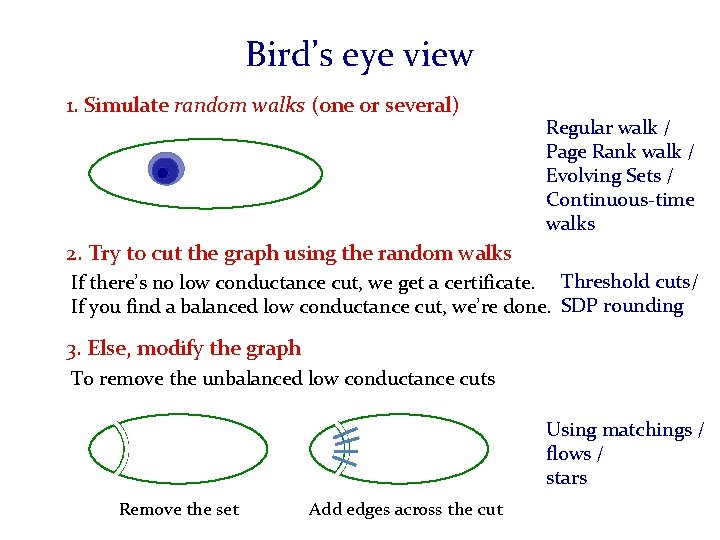
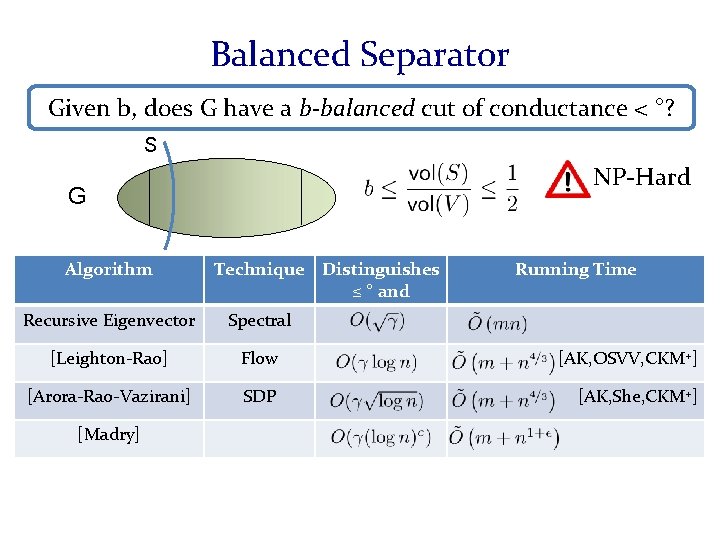
Graph Cuts and Random Walks Intimate connection between Graph cuts and Random walks. [Mihail] Given the distribution of a random walk that has mixed, can find a cut S with in time. [Alon-Milman][Mihail][Lovasz-Simonovits][Spielman-Teng] Page Rank Usual Random [Anderson-Chung-Lang] Evolvingwalks Sets. Walks on a graph Random [Andersen-Peres] Random Walks Continuous Time [Orecchia-Vishnoi][this talk]… Random Walks

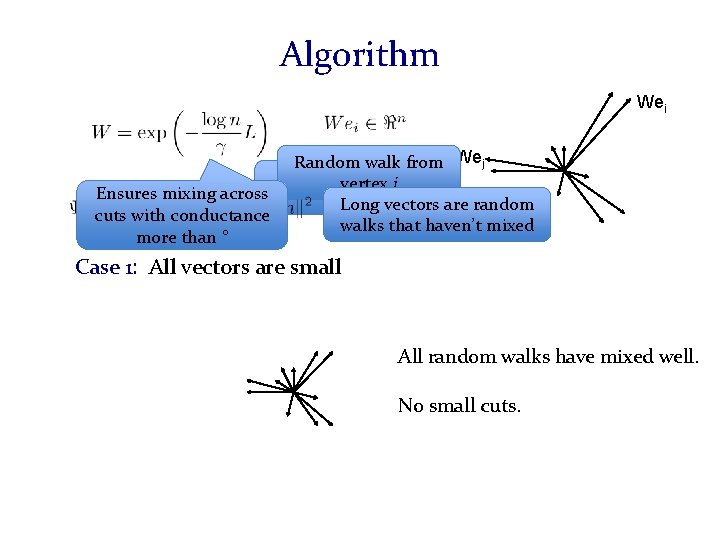
Bird’s eye view 1. Simulate random walks (one or several) Regular walk / Page Rank walk / Evolving Sets / Continuous-time walks 2. Try to cut the graph using the random walks If there’s no low conductance cut, we get a certificate. Threshold cuts/ If you find a balanced low conductance cut, we’re done. SDP rounding 3. Else, modify the graph To remove the unbalanced low conductance cuts Using matchings / flows / stars Remove the set Add edges across the cut

Continuous Time Random Walks Given initial distribution , Heat-Kernel random walk Random walk of Thm. We can reduce Balanced Separator to simulating length l ~ Poisson(t) heat-kernel random walks with e-x is a nice function. Track progress using Previous a Whyresults heat-kernel Techniques fromhad SDPs[OV], Golden Thompson inequality [AK] poly(1/°) dependence randomupdates walk? aka exponential Don’t know such a result for other random walks Matrix Mult. Weights [AK]

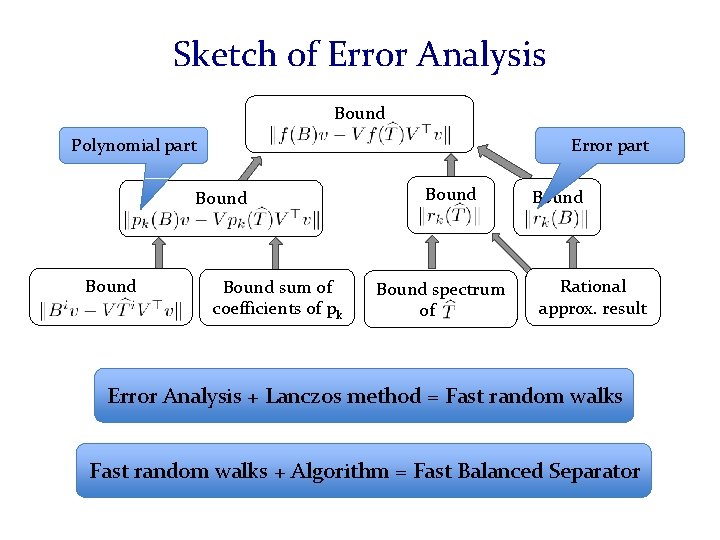
Algorithm Wei Random walk from Wej vertex i Ensures mixing across. An embedding in Long vectors are random cuts with conductance walks that haven’t mixed more than ° Case 1: All vectors are small All random walks have mixed well. No small cuts.

Algorithm Case 2: Walks have not mixed Wei Wej Random Projection + Threshold Cut “Cheeger Rounding” If we find a balanced cut of small conductance , we’re done. ELSE

Algorithm Case 2 b: Walks have not mixed (and we didn’t find a balanced cut) Wei Wej We can find a ball cut S S S is the union of “all unbalanced low conductance cuts”

Algorithm Case 2 b: Walks have not mixed (and we didn’t find a balanced cut) Wei Wej We can find a ball cut S S Add edges from all vertices outside the ball to all inside For efficiency, we use JL lemma and work with of Soft removal Goal: Given L, ¿, v. L, ¿ , v. Compute Approximate O(log n) dimensional embeddings. [AK] cuts unbalanced O(log n) rounds

SIMULATING RANDOM WALKS

Approximating Heat-Kernel Goal: Given ¿, L, v, ±, find u s. t. walk Taylor Series Approx. ? Heat-Kernel random Small Used in previous algorithms Need Too Slow required by algorithm error suffices for the algorithm

Approximating Heat-Kernel Goal: Given ¿, L, v, ±, find u s. t. Better polynomials? YES!! It suffices to approximate e-x on [Thm] There exists a polynomial p of degree such that [Thm] Given G that has a balanced cut of conductance , we can find one of conductance in time Better guarantee, same running Still not near-linear! time as [Andersen-Peres]

Approximating Heat-Kernel Goal: Given ¿, L, v, ±, find u s. t. Even better polynomials? Not Really! [Thm] Any polynomial such that requires degree Simple proof using Markov’s theorem

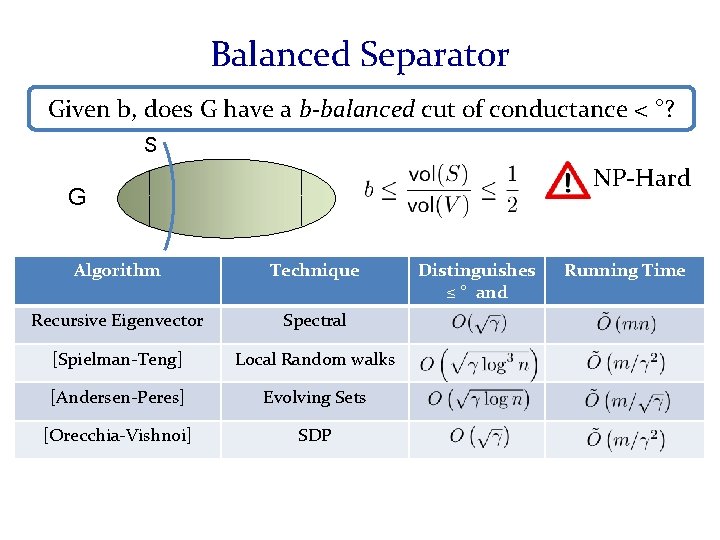
Beyond Polynomials Rational Functions! [Saff-Schönhage-Varga] There is a degree k polynomial pk such that Infinite Interval! Approximating up to error ± Geometric Decay! Computing. Need degree vectors Can use [Spielman-Teng]! [Spielman-Teng] [Thm] Given ¿, L, (Informal) v, ±, we can compute u such that -1 y in We can approximate (c. I+L) time. in time Assume: knew pk is explicitly Two Issues: 1. We [SSV] result existential 2. 2. ST exact STcomputationwas is approximate We’re DONE!

“But we don’t know the polynomial. ” LANCZOS’ METHOD

Lanczos’ Method Let Define f so that Goal: Approximate f(B)v as well as any degree k poly. From real approximation to matrices Lanczos Method Existence of a good approximate poly suffices Small degree implies efficiency

Lanczos’ Method Goal: Approximate f(B)v as well as any degree k poly. p – any degree k polynomial Observe Let Krylov Subspace · of order k be an orthonormal basis for · (k+1) x (k+1) matrix Let T be the operator B restricted to · For any degree k polynomial p, Let Projection on · T is a much smaller matrix! Our guess:

Error Guarantee Goal: Bound the norm of the error Suppose p(x) is a good degree k approximation to f Let the error be Equal! * error of best degree k polynomial approximation Don’t even need to know the polynomial! Bounded by r on B +Spectrum(B) Construct basis +Spectrum(T) Diagonalize Cost = k mult. by for our setting Since T is B restricted to ·, Spectrum(T) is bounded by Spectrum(B) T

What about the error? HANDLING APPROXIMATE COMPUTATION

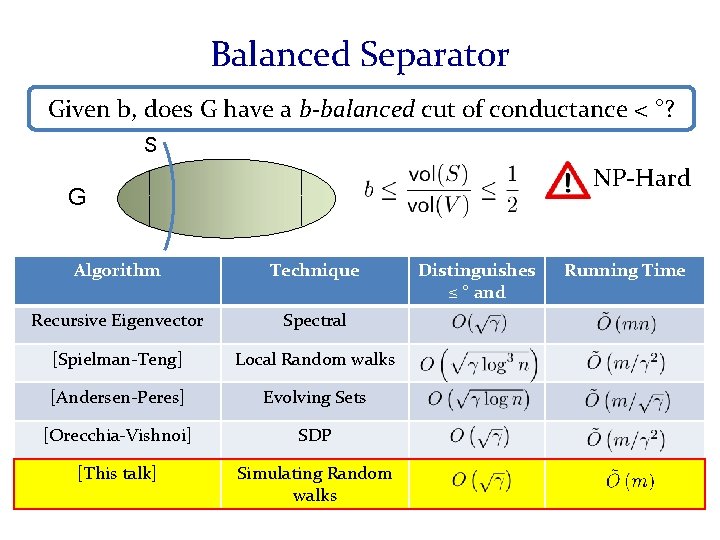
Why Lanczos is insufficient We needed to compute an orthonormal basis for [ST] computation is only approximate Multiplication with is only approximate Subspace · is approximate. & Operator T is approximate T is not even symmetric! We symmetrize. Compute approximation with We bound the error We lose nice spectral properties

Sketch of Error Analysis Bound Polynomial part Error part Bound sum of coefficients of pk Bound spectrum of Bound Rational approx. result Error Analysis + Lanczos method = Fast random walks + Algorithm = Fast Balanced Separator

Conclusions • Reduced balanced separator to simulating heat-kernel random walks • Approximated the heat kernel random walk in time. • Can be used as primitives for designing nearlinear time algorithms.

Open Questions • • Other applications of fast matrix exponentiation Linear-time Graph decomposition? Linear time algorithms for small set expansion? Linear time algorithm for approximation for Balanced Separator

Thank you!

An Important Tool [Christiano et al. ] s-t MAXFLOW s-t MINCUT Solving Laplacian Linear Systems Electrical Flows Solve Linear Systems Lx=y Gaussian Elimination / Direct Methods Cholesky Decomposition is a 3)graph Too slow. LO(n time Laplacian Hopeless Conjugate Gradient Iterative methods Approximate method. time [Spielman-Teng] (Informal) We can approximate L-1 y in time. Other Applications – Approximating second eigenvector Balanced graph partitioning, [Spielman-Teng], Cover times [Ding-Lee-Peres], Generating Simulating continuous-time random walks random spanning trees[Madry-Kelner], Graph Sparsification [This talk] [Spielman-Srivastava]

Beyond Polynomials Rational Functions! [Saff-Schönhage-Varga] There is a degree k polynomial pk such that Infinite Interval! L 1 bound on [0, 1) on [-1, 1] L 1 bound on [-1, 1] Geometric Decay! L 2 bound Small required degree. on [-1, 1] Write. Cauchy Change function Schwarz Interval as an integral Two Assume: Issues: 1. 1. We Wedon’t knewknow pk explicitly 2. 2. STSTSolverwas is approximate exact We’re DONE!

Faster Simulation Polynomials don’t suffice, then, how do we simulate the random walk fast?

Lanczos Method Goal: Given symmetric B, v, k, and function f; approximate f(B)v as well as any degree k poly p – any degree k polynomial Observe Let k-Identity Krylov Subspace · of order k For any degree k polynomial p, be an orthonormal basis for · Projection on · Our guess: T is a much smaller matrix!

Error Guarantee Goal: Bound the norm of the error Write Equal! Any degree k polynomial As good as the best degree k polynomial! The columns of V are orthnormal True for any p!! Since and the columns of V are orthnormal, Cost = k mult. by B + Construct basis + Diagonalize T if B is a Laplacian

Using Lanczos for our Algorithm Goal: Given A, wanted to approximate as Use Lanczos with suffices. Still need to address the issue of approximate multiplication with