Linear Techniques for Regression and Classification on Functional

Linear Techniques for Regression and Classification on Functional Data Gilbert Saporta Chaire de Statistique Appliquée & CEDRIC Conservatoire National des Arts et Métiers 292 rue Saint Martin F 75141 Paris Cedex 03 saporta@cnam. fr http: //cedric. cnam. fr/~saporta Joint work with D. Costanzo (U. Calabria) & C. Preda (U. Lille 2) Open University, Milton Keynes, May 17, 2007

Outline 1. Introduction 2. OLS regression on functional data 3. PLS functional regression 4. Clusterwise regression 5. Discrimination 6. Anticipated prediction 7. Conclusion and perspectives Open University, Milton Keynes, May 17, 2007 2

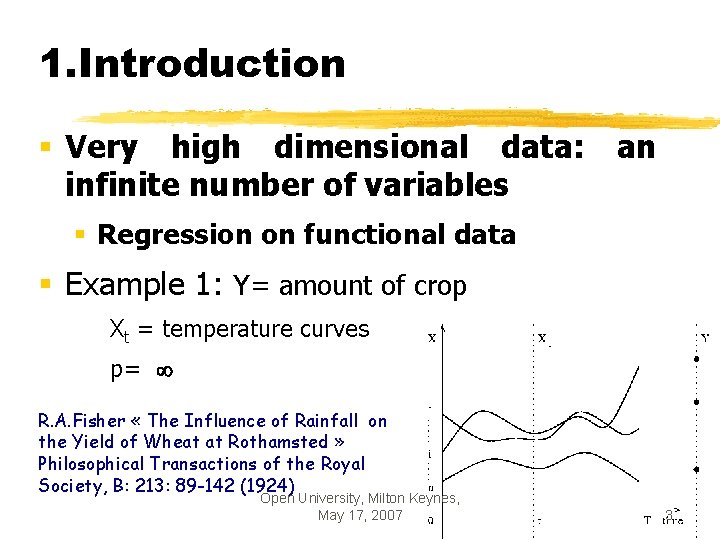
1. Introduction § Very high dimensional data: an infinite number of variables § Regression on functional data § Example 1: Y= amount of crop Xt = temperature curves p= R. A. Fisher « The Influence of Rainfall on the Yield of Wheat at Rothamsted » Philosophical Transactions of the Royal Society, B: 213: 89 -142 (1924) Open University, Milton Keynes, May 17, 2007 3

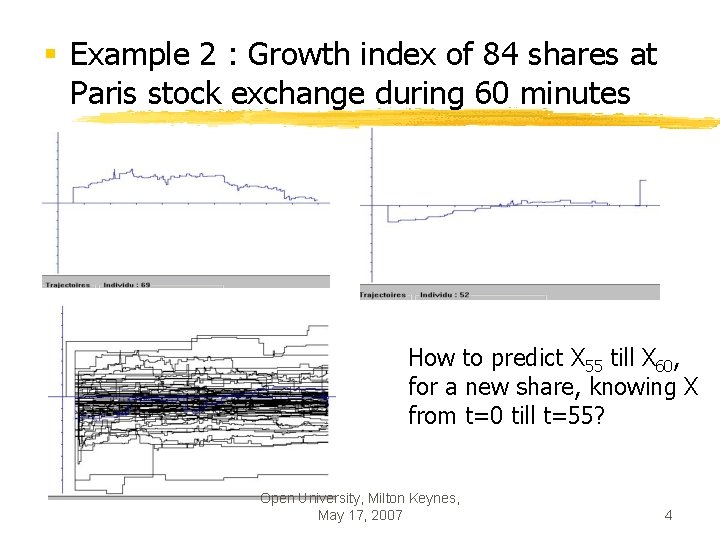
§ Example 2 : Growth index of 84 shares at Paris stock exchange during 60 minutes How to predict X 55 till X 60, for a new share, knowing X from t=0 till t=55? Open University, Milton Keynes, May 17, 2007 4

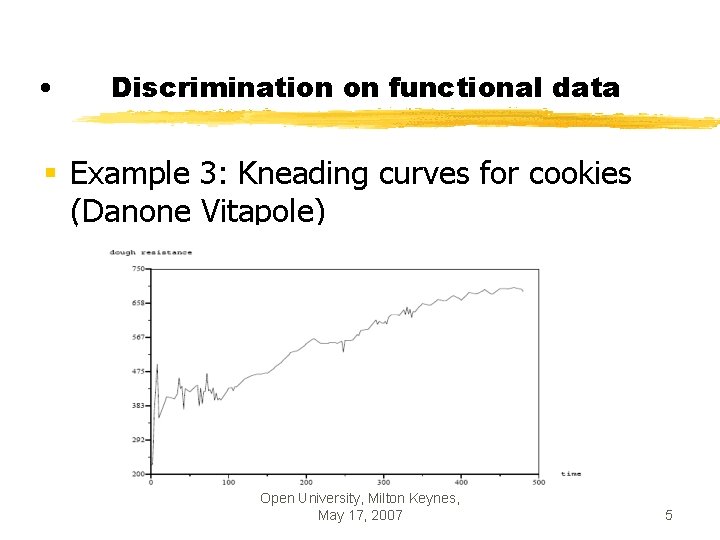
• Discrimination on functional data § Example 3: Kneading curves for cookies (Danone Vitapole) Open University, Milton Keynes, May 17, 2007 5

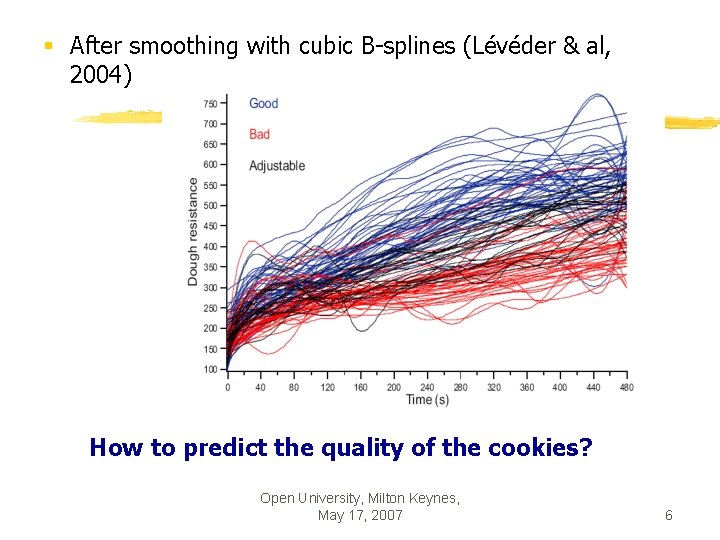
§ After smoothing with cubic B-splines (Lévéder & al, 2004) How to predict the quality of the cookies? Open University, Milton Keynes, May 17, 2007 6

§ Linear combination § « Integral regression » (Fisher 1924) § instead of a finite sum Open University, Milton Keynes, May 17, 2007 7

§ Discrimination on functional data § Particular case of regression when the response is binary § Anticipation § Determine an optimal time t*<T giving a prediction based on [0; t*] almost as good as the prediction using all the data [0; T] Open University, Milton Keynes, May 17, 2007 8

2. OLS regression on functional data § Y ; Xt (with zero mean) 2. 1 The OLS problem § Minimizing leads to normal, or Wiener-Hopf, equations: where C(t, s)= cov(Xt, Xs)=E(Xt. Xs) Open University, Milton Keynes, May 17, 2007 9

2. 2 Karhunen-Loeve decomposition (functional PCA) § factor loadings: § principal components: Open University, Milton Keynes, May 17, 2007 10

§ Picard’s theorem: is unique if and only if: § Generally not true…especially when n is finite: since p >n. Perfect fit when minimizing: Open University, Milton Keynes, May 17, 2007 11

§ Even if is unique, Wiener-Hopf equation is not an ordinary integral equation: the solution is more frequently a distribution than a function § Constrained solutions are needed. (cf Green & Silverman 1994, Ramsay & Silverman 1997). Open University, Milton Keynes, May 17, 2007 12

2. 3 Regression on principal components § Rank q approximation: Open University, Milton Keynes, May 17, 2007 13

Numerical computations § Solve integral equations in the general case § for step functions: finite number of variables and of units: operators are matrices, but with a very high size § Approximations by discretisation of time Open University, Milton Keynes, May 17, 2007 14

§ Which principal components? § First q? § q best correlated with Y? § Principal components are computed irrespective of the response… Open University, Milton Keynes, May 17, 2007 15

3. Functional PLS regression § Use PLS components instead of principal components. § first PLS component : § further PLS components as usual Open University, Milton Keynes, May 17, 2007 16

§ order q approximation of Y by Xt : § Convergence theorem: § q have to be finite in order to get a formula! § Usually q is selected by cross-validation (Preda & Saporta, 2005 a) Open University, Milton Keynes, May 17, 2007 17

§ First PLS component easily interpretable: coefficients with the same sign as r(y; xt) § No integral equation § PLS fits better than PCR: Same proof as in De Jong, 1993 Open University, Milton Keynes, May 17, 2007 18

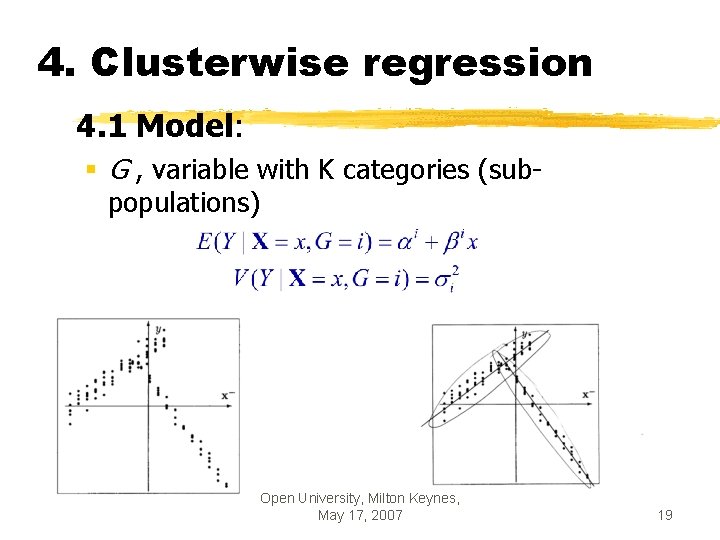
4. Clusterwise regression 4. 1 Model: § G , variable with K categories (subpopulations) Open University, Milton Keynes, May 17, 2007 19

§ 4. 2 OLS and clusterwise regression § Residual variance of global regression= within cluster residual variance + variance due to the difference between local (clusterwise) and global regression (OLS) Open University, Milton Keynes, May 17, 2007 20

§ 4. 3 Estimation (Charles, 1977) § number of clusters k needs to be known § Alternated least squares § For a given partition: estimate linear regressions for each cluster § Reallocate each point to the closest regression line (or surface) § Equivalent to ML for fixed regressors, fixed partition model (Hennig, 2000) § 4. 4 Optimal k § AIC, BIC, crossvalidation Open University, Milton Keynes, May 17, 2007 21

4. 5 Clusterwise functional PLS regression § OLS functional regression not adequate to give estimations in each cluster § Our proposal: estimate local models with functional PLS regression § Is the clusterwise algorithm still consistent? § Proof in Preda & Saporta, 2005 b Open University, Milton Keynes, May 17, 2007 22

§ Prediction: § Allocate a new observation to a cluster (nearest neighbor or other classification technique) § Use the corresponding local model § May be generalised if Y is itself a random vector: Open University, Milton Keynes, May 17, 2007 23

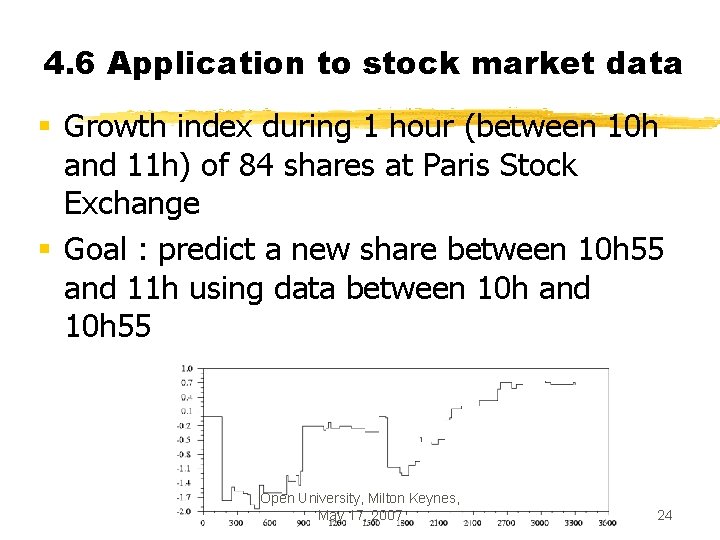
4. 6 Application to stock market data § Growth index during 1 hour (between 10 h and 11 h) of 84 shares at Paris Stock Exchange § Goal : predict a new share between 10 h 55 and 11 h using data between 10 h and 10 h 55 Open University, Milton Keynes, May 17, 2007 24

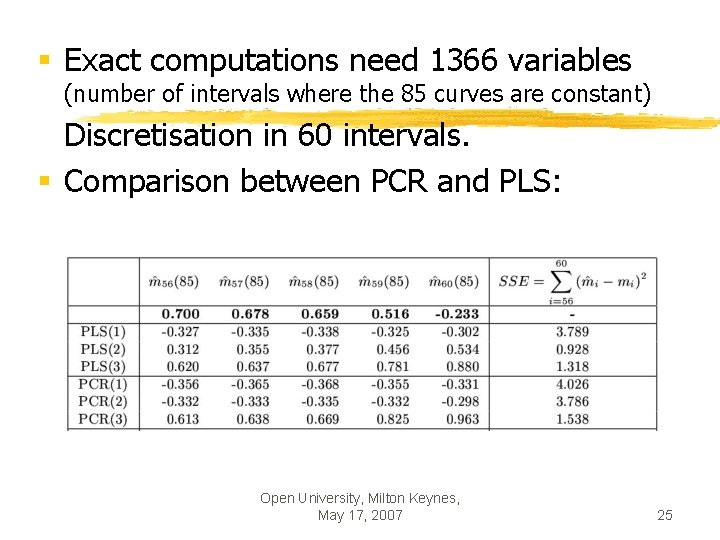
§ Exact computations need 1366 variables (number of intervals where the 85 curves are constant) Discretisation in 60 intervals. § Comparison between PCR and PLS: Open University, Milton Keynes, May 17, 2007 25

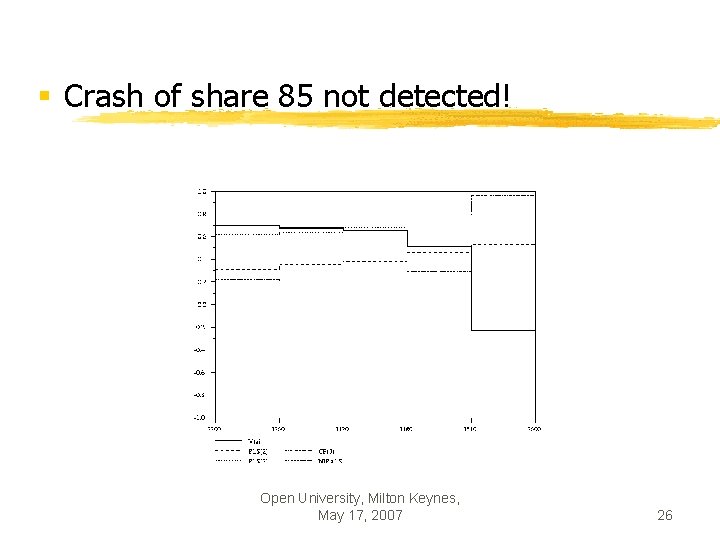
§ Crash of share 85 not detected! Open University, Milton Keynes, May 17, 2007 26

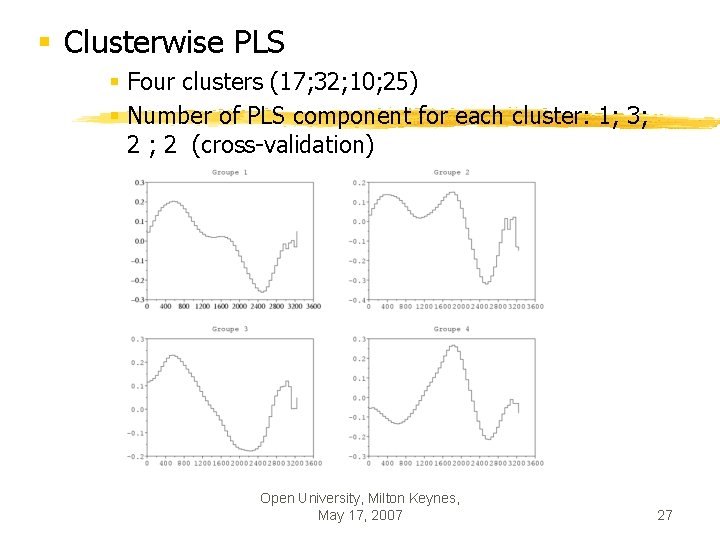
§ Clusterwise PLS § Four clusters (17; 32; 10; 25) § Number of PLS component for each cluster: 1; 3; 2 (cross-validation) Open University, Milton Keynes, May 17, 2007 27

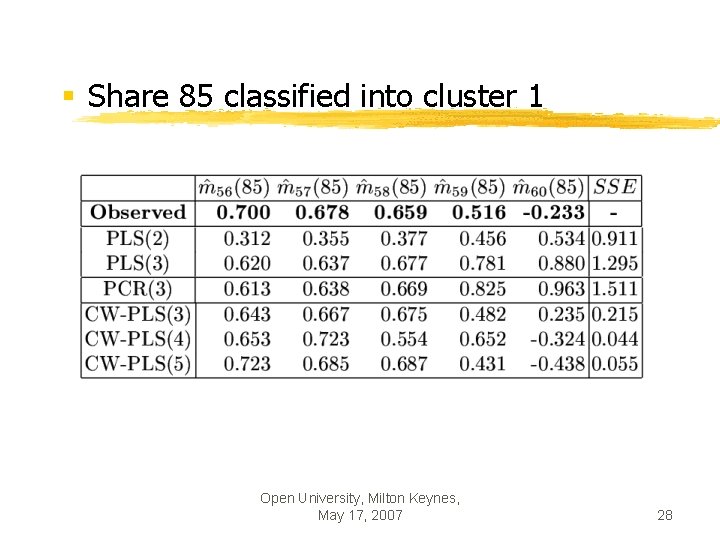
§ Share 85 classified into cluster 1 Open University, Milton Keynes, May 17, 2007 28

3. Functional linear discrimination § LDA : linear combinations maximizing the ratio Between group variance /Within group variance § For 2 groups Fisher’s LDF via a regression between coded Y and Xt eg (Preda & Saporta, 2005 a) Open University, Milton Keynes, May 17, 2007 29

§ PLS regression with q components gives an approximation of β(t) and of the score § For more than 2 groups: PLS 2 regression between k-1 indicators of Y and Xt § First PLS component given by the first eigenvector of the product of Escoufier operators Wx. WY Preda & Saporta, 2002 and Barker & Rayens , 2003 Open University, Milton Keynes, May 17, 2007 30

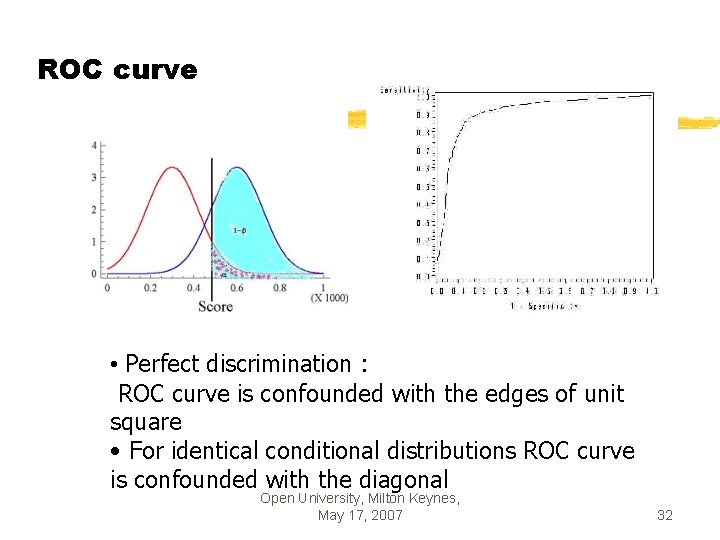
Quality measures § For k=2 : ROC curve and AUC § For a specific threshold, x is classified into G 1 if d. T(x)>s § Sensitivity or true positive rate: P(d. T(x)>s/Y=1)=1 -β § 1 - specificity or 1 - true negative rate: P(d. T(x)>s/Y=0)= Open University, Milton Keynes, May 17, 2007 31

ROC curve • Perfect discrimination : ROC curve is confounded with the edges of unit square • For identical conditional distributions ROC curve is confounded with the diagonal Open University, Milton Keynes, May 17, 2007 32

§ ROC curve invariant for any increasing monotonous transformation § Area under ROC curve: a global measure of performance allowing model comparisons (partially) § X 1 drawn from G 1 and X 2 from G 2 § AUC estimated by the proportion of concordant pairs § nc : Wilcoxon-Mann-Whitney statistic U+W= n 1 n 2+0. 5 n +1) Milton. AUC=U/n 1(n 1 1 n 2 Open University, Keynes, May 17, 2007 33

4. Anticipated prediction § t*<T such that the analysis on [0; t*] give donne predictions almost as good as with [0; T] § Solution: § When increasing s from 0 to T, look for the first value such that AUC(s) does not differ significantly from AUC(T) Open University, Milton Keynes, May 17, 2007 34

§ A bootstrap procedure § Stratified resampling of the data § For each replication b, AUCb(s) and AUCb(T) are computed § Student’s T test or Wilcoxon on the B paired differences b=AUCb(s)- AUCb(T) Open University, Milton Keynes, May 17, 2007 35

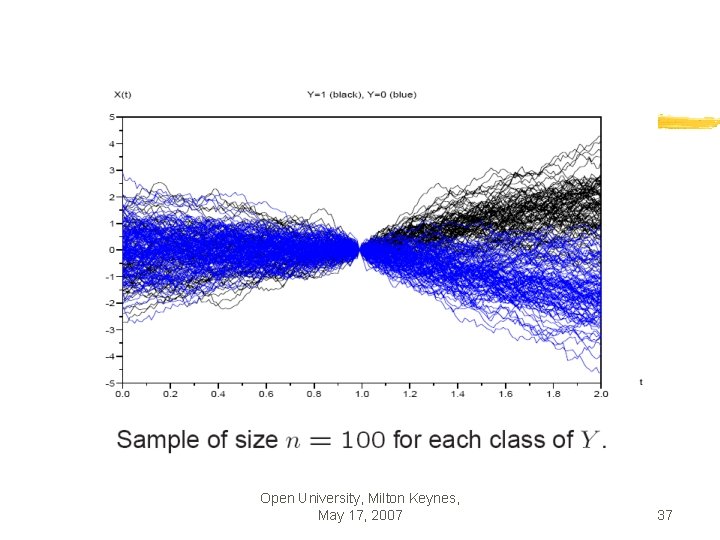
5. Applications § 5. 1 simulated data § Two classes with equal priors § W(t) brownian motion Open University, Milton Keynes, May 17, 2007 36

Open University, Milton Keynes, May 17, 2007 37

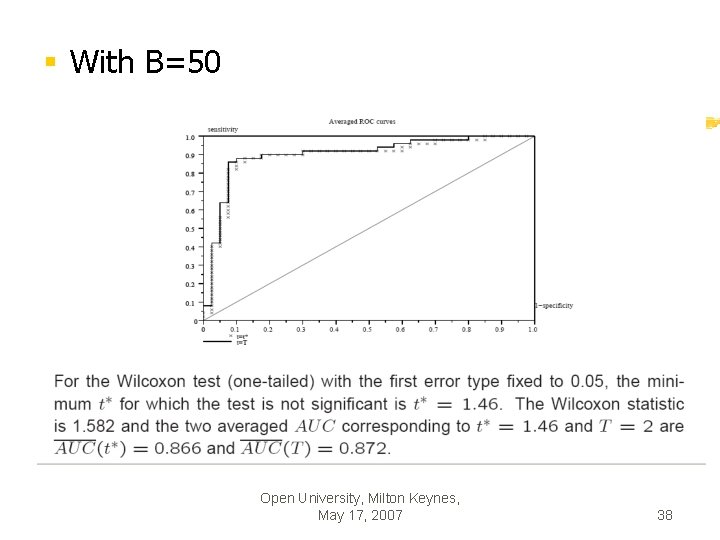
§ With B=50 Open University, Milton Keynes, May 17, 2007 38

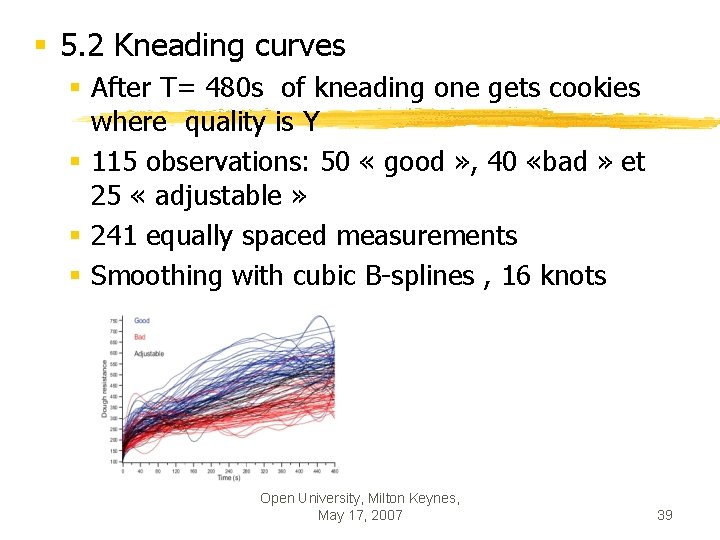
§ 5. 2 Kneading curves § After T= 480 s of kneading one gets cookies where quality is Y § 115 observations: 50 « good » , 40 «bad » et 25 « adjustable » § 241 equally spaced measurements § Smoothing with cubic B-splines , 16 knots Open University, Milton Keynes, May 17, 2007 39

§ Performance for Y={good, bad} § Repeat 100 times the split into learning and test samples of size (60, 30) § Average error rate § 0. 142 with principal components § 0. 112 with PLS components § Average AUC = 0. 746 β(t) Open University, Milton Keynes, May 17, 2007 40

§ Anticipated prediction § B=50 § t*=186 § The recording period of the resistance dough can be reduced to less than half of the current one Open University, Milton Keynes, May 17, 2007 41

6. Conclusions and perspectives § PLS regression is an efficient and simple way to get linear prediction for functional data § We have proposed a bootstrap procedure for the problem of anticipated prediction Open University, Milton Keynes, May 17, 2007 42

§ Works in progress: § « on-line » forecasting: instead of using the same anticipated decision time t* for all data, we could adapt t* to each new trajectory given its incoming measurements. § Clusterwise discrimination § Comparison with functional logistic regression Aguilera et al, 2006 Open University, Milton Keynes, May 17, 2007 43

References § § § § § Aguilera A. M. , Escabias, M. & Valderrama M. J. (2006) Using principal components for estimating logistic regression with high-dimensional multicollinear data, Computational Statistics & Data Analysis, 50, 1905 -1924 Barker M. , Rayens W. (2003) Partial least squares for discrimination. J Chemomet 17: 166– 173 Charles, C. , 1977. Régression typologique et reconnaissance des formes. Ph. D. , Université Paris IX. D. Costanzo, C. Preda et G. Saporta (2006). Anticipated prediction in discriminant analysis on functional data for binary response. In COMPSTAT 2006, p. 821 -828, Physica-Verlag Hennig, C. , (2000). Identifiability of models for clusterwise linear regression. J. Classification 17, 273– 296. Lévéder C. , Abraham C. , Cornillon P. A. , Matzner-Lober E. , Molinari N. (2004): Discrimination de courbes de pétrissage. Chimiometrie 2004, 37– 43. Preda C. , Saporta G. (2005 a): PLS regression on a stochastic process, Computational Statistics and Data Analysis, 48, 149 -158. Preda C. , Saporta G. (2005 b): Clusterwise PLS regression on a stochastic process, Computational Statistics and Data Analysis, 49, 99 -108. Preda C. , Saporta G. & Lévéder C. , (2007) PLS classification of functional data, Computational Statistics Ramsay & Silverman (1997) Functional data analysis, Springer Open University, Milton Keynes, May 17, 2007 44