Linear Systems Numerical Methods Linear equations N unknowns

Linear Systems Numerical Methods

Linear equations • N unknowns, M equations coefficient matrix where

Determinants and Cramer’s Rule [A] : coefficient matrix D : Determinant of A matrix 3

Solving methods • Direct methods – Gauss elimination – Gauss-Jordan elimination – LU decomposition – Singular value decomposition –… • Iterative methods – Jacobi iteration – Gauss-Seidel iteration –…

Linear Systems • Solve Ax=b, where A is an n n matrix and b is an n 1 column vector • Can also talk about non-square systems where A is m n, b is m 1, and x is n 1 – Overdetermined if m>n: “more equations than unknowns” – Underdetermined if n>m: “more unknowns than equations” Can look for best solution using least squares

Gauss Elimination • Solve Ax = b • Consists of two phases: –Forward elimination –Back substitution • Forward Elimination reduces Ax = b to an upper triangular system Tx = b’ • Back substitution can then solve Tx = b’ for x 6 Forward Elimination Back Substitution

Gauss Elimination • Fundamental operations: 1. Replace one equation with linear combination of other equations 2. Interchange two equations 3. Re-label two variables • Combine to reduce to trivial system • Simplest variant only uses #1 operations, but get better stability by adding #2 (partial pivoting) or #2 and #3 (full pivoting)

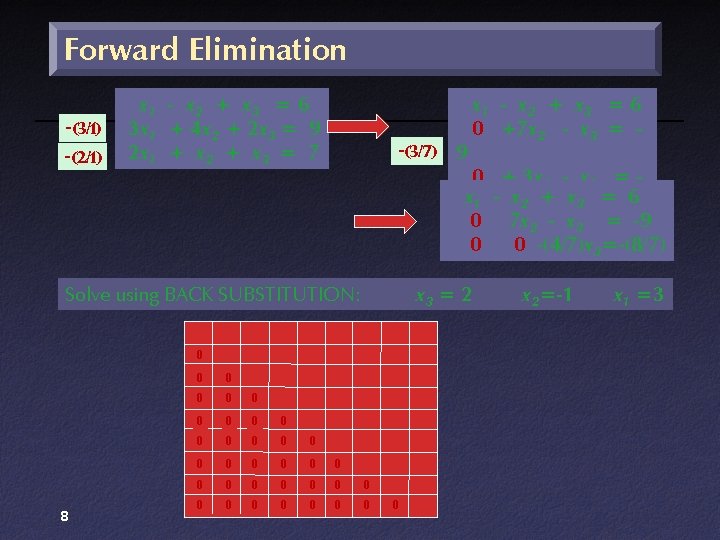
Forward Elimination Gaussian Elimination -(3/1) -(2/1) x 1 - x 2 + x 3 = 6 3 x 1 + 4 x 2 + 2 x 3 = 9 2 x 1 + x 2 + x 3 = 7 -(3/7) x 1 - x 2 + x 3 = 6 0 +7 x 2 - x 3 = 9 0 + 3 x 2 - x 3 = 5 x 1 - x 2 + x 3 = 6 0 7 x 2 - x 3 = -9 0 0 -(4/7)x 3=-(8/7) Solve using BACK SUBSTITUTION: x 3 = 2 0 8 0 0 0 0 0 0 0 0 0 x 2=-1 x 1 =3

Back Substitution 1 x 0 +1 x 1 – 1 x 2 +4 x 3 = 8 – 2 x 1 – 3 x 2 +1 x 3 = 5 2 x 2 – 3 x 3 = 0 2 x 3 = 4 x 3 = 2 9

Back Substitution 1 x 0 +1 x 1 – 1 x 2 = 0 – 2 x 1 – 3 x 2 = 3 2 x 2 = 6 x 2 = 3 10

Back Substitution 1 x 0 x 1 = – 6 11 +1 x 1 = 3 – 2 x 1 = 12

Back Substitution x 0 = 9 1 x 0 = 9

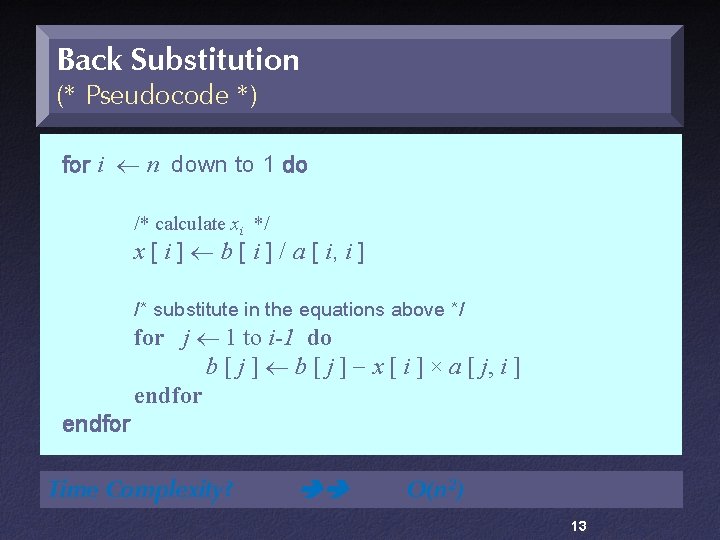
Back Substitution (* Pseudocode *) for i n down to 1 do /* calculate xi */ x [ i ] b [ i ] / a [ i, i ] /* substitute in the equations above */ endfor j 1 to i-1 do b [ j ] x [ i ] × a [ j, i ] endfor Time Complexity? O(n 2) 13

M U L T I P L I E R S Forward Elimination 4 x 0 +6 x 1 +2 x 2 – 2 x 3 = 8 +5 x 2 – 2 x 3 = 4 -(2/4) 2 x 0 -(-4/4) – 4 x 0 – 3 x 1 – 5 x 2 +4 x 3 = 1 -(8/4) 8 x 0 +18 x 1 – 2 x 2 +3 x 3 = 40 14

Forward Elimination M U L T I P L I E R S 15 4 x 0 +6 x 1 +2 x 2 – 2 x 3 = 8 – 3 x 1 +4 x 2 – 1 x 3 = 0 -(3/-3) +3 x 1 – 3 x 2 +2 x 3 = 9 -(6/-3) +6 x 1 – 6 x 2 +7 x 3 = 24

Forward Elimination 4 x 0 M U L T I P L I E R ? ? 16 +6 x 1 +2 x 2 – 2 x 3 = 8 – 3 x 1 +4 x 2 – 1 x 3 = 0 1 x 2 +1 x 3 = 9 2 x 2 +5 x 3 = 24

Forward Elimination 4 x 0 17 +6 x 1 +2 x 2 – 2 x 3 = 8 – 3 x 1 +4 x 2 – 1 x 3 = 0 1 x 2 +1 x 3 = 9 3 x 3 = 6

Gauss-Jordan Elimination a 11 0 0 0 0 b 11 0 x 22 0 0 0 0 b 22 0 0 x 33 0 0 0 b 33 0 0 0 x 44 0 0 0 b 44 0 0 x 55 0 0 b 55 0 0 0 x 66 0 0 0 b 66 0 0 0 x 77 0 0 b 77 0 0 0 0 x 88 0 b 66 0 0 0 0 x 99 b 66 18

Gauss-Jordan Elimination: Example Scaling R 2: R 2/(-1) R 2 - (-1)R 1 R 3 - ( 3)R 1 - (1)R 2 Scaling R 3: R 3/(18) R 3 -(4)R 2 R 1 - (7)R 3 RESULT: R 2 -(-5)R 3 x 1=8. 45, 19 Time Complexity? O(n 3) x 2=-2. 89, x 3=1. 23

Gauss-Jordan Elimination • Solve: • Only care about numbers – form “tableau” or “augmented matrix”:

Gauss-Jordan Elimination • Given: • Goal: reduce this to trivial system and read off answer from right column

Gauss-Jordan Elimination • Basic operation 1: replace any row by linear combination with any other row • Here, replace row 1 with 1/2 * row 1 + 0 * row 2

Gauss-Jordan Elimination • Replace row 2 with row 2 – 4 * row 1 • Negate row 2

Gauss-Jordan Elimination • Replace row 1 with row 1 – 3/2 * row 2 • Read off solution: x 1 = 2, x 2 = 1

Augmented Matrices • Matrices are rectangular arrays of numbers that can aid us by eliminating the need to write the variables at each step of the reduction. • For example, the system Coefficie nt Matrix may be represented by the augmented matrix

Matrices and Gauss-Jordan • Every step in the Gauss-Jordan elimination method can be expressed with matrices, rather than systems of equations, thus simplifying the whole process: • Steps expressed as systems of equations: Toggle slides back and forth to compare before and changes • Steps expressed as augmented matrices:

Matrices and Gauss-Jordan • Every step in the Gauss-Jordan elimination method can be expressed with matrices, rather than systems of equations, thus simplifying the whole process: • Steps expressed as systems of equations: Toggle slides back and forth to compare before and changes • Steps expressed as augmented matrices:

Matrices and Gauss-Jordan • Every step in the Gauss-Jordan elimination method can be expressed with matrices, rather than systems of equations, thus simplifying the whole process: • Steps expressed as systems of equations: Toggle slides back and forth to compare before and changes • Steps expressed as augmented matrices:

Matrices and Gauss-Jordan • Every step in the Gauss-Jordan elimination method can be expressed with matrices, rather than systems of equations, thus simplifying the whole process: • Steps expressed as systems of equations: Toggle slides back and forth to compare before and changes • Steps expressed as augmented matrices:

Matrices and Gauss-Jordan • Every step in the Gauss-Jordan elimination method can be expressed with matrices, rather than systems of equations, thus simplifying the whole process: • Steps expressed as systems of equations: Toggle slides back and forth to compare before and changes • Steps expressed as augmented matrices:

Matrices and Gauss-Jordan • Every step in the Gauss-Jordan elimination method can be expressed with matrices, rather than systems of equations, thus simplifying the whole process: • Steps expressed as systems of equations: Toggle slides back and forth to compare before and changes • Steps expressed as augmented matrices:

Matrices and Gauss-Jordan • Every step in the Gauss-Jordan elimination method can be expressed with matrices, rather than systems of equations, thus simplifying the whole process: • Steps expressed as systems of equations: Toggle slides back and forth to compare before and changes • Steps expressed as augmented matrices:

Matrices and Gauss-Jordan • Every step in the Gauss-Jordan elimination method can be expressed with matrices, rather than systems of equations, thus simplifying the whole process: • Steps expressed as systems of equations: Toggle slides back and forth to compare before and changes • Steps expressed as augmented matrices:

Matrices and Gauss-Jordan • Every step in the Gauss-Jordan elimination method can be expressed with matrices, rather than systems of equations, thus simplifying the whole process: • Steps expressed as systems of equations: Toggle slides back and forth to compare before and changes Row Reduced Form of the Matrix • Steps expressed as augmented matrices: