Linear sorts Counting sort Radix sort cs 333cutler

Linear sorts Counting sort Radix sort cs 333/cutler Counting sort 1

Pigeonhole Sort Pigeonhole-Sort( A, k)//keys range 1. . k, A[1. . n] 1. for i 1 to k //initialize C 2. C[i ] 0 3. for j 1 to length[A] 4. C[A[ j ] ] + 1 //Count keys 5. q 1 6. for j 1 to k //rewrite A 7. while C[j]>0 8. A[q] j 9. C[ j ]-1 10. q q+1 cs 333/cutler Counting sort 2

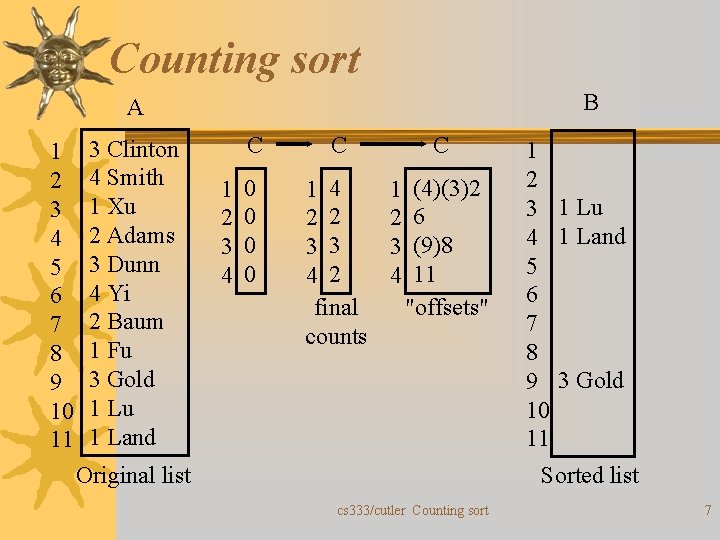
Counting sort ¬ Problem: Sort n records stored in A[1. . n] – Each record contains a key and data – All keys are in the range of 1 to k ¬ Main idea: 1. Count in C, number records with key = i, i = 1, …, k. 2. Use counts in C to compute the offset in sorted B of record with key i for i = 1, …, k. 3. Copy A into sorted B using and updating (decrementing) the computed offsets. To make the sort stable we start at last position of A. cs 333/cutler Counting sort 3

Counting sort ¬ Additional Space – The sorted list is stored in B – Additional array C of size k ¬ Note: Pigeonhole sort does not require array B cs 333/cutler Counting sort 4

How shall we compute the offsets? ¬ Assume C[1]= 3 (then 3 records with key=1 should be stored in positions 1, 2, 3 in the sorted array B). We keep the offset for key 1 = 3. ¬ Let C[2]=2 (then 2 records with key=2 should be in stored in positions 4, 5 in B). ¬ We compute the offset for key 2 to be (C[2] + offset for key 1) = 2 +3 = 5 ¬ In general offset for key i is (C[i] + offset for key i-1). cs 333/cutler Counting sort 5

Counting Sort Counting-Sort( A, B, k) 1. for i 1 to k //initialize C 2. C[i ] 0 3. for j 1 to length[A] 4. C[A[ j ] ] + 1 //Count keys 5. for i 2 to k 6. C[i ] +C[i -1] //Compute offset 7. for j length[A] downto 1 //copy 8. B [ C[A[ j ] ] ] A[ j ] 9. C[A[ j ] ] ] C [A[ j ] ] – 1//update offset cs 333/cutler Counting sort 6

Counting sort B A 1 2 3 4 5 6 7 8 9 10 11 3 Clinton 4 Smith 1 Xu 2 Adams 3 Dunn 4 Yi 2 Baum 1 Fu 3 Gold 1 Lu 1 Land 1 2 3 4 C C 0 0 1 4 2 2 3 3 4 2 final counts C 1 2 3 4 (4)(3)2 6 (9)8 11 "offsets" 1 2 3 1 Lu 4 1 Land 5 6 7 8 9 3 Gold 10 11 Sorted list Original list cs 333/cutler Counting sort 7

Analysis: ¬O(k + n) time – What if k = O(n) ¬Requires k + n extra storage. ¬Stable sort: Preserves the original order of equal keys. ¬Is counting sort stable? ¬Is counting sort good for sorting records with 32 bit keys? cs 333/cutler Counting sort 8

Radix Sort ¬Some history ¬The algorithm cs 333/cutler Counting sort 9

Hollerith’s punched cards ¬Hollerith devised what was to become the computer punched card ¬Each card has 12 rows and 80 columns ¬Each column represents a single alphanumeric character or symbol. ¬The card punching machine punches holes in some of the 12 positions of each column cs 333/cutler Counting sort 10

A punched card cs 333/cutler Counting sort 11

IBM Card card punchingmachine cs 333/cutler Counting sort 12

Hollerith’s tabulating machines ¬ As the cards were fed through a "tabulating machine, " pins passed through the positions where holes were punched completing an electrical circuit and subsequently registered a value. ¬ The 1880 census in the U. S. took seven years to complete ¬ With Hollerith's "tabulating machines" the 1890 census took the Census Bureau six weeks ¬ Through mergers company’s name - IBM cs 333/cutler Counting sort 13

Card sorting machine IBM’s card sorting machine cs 333/cutler Counting sort 14

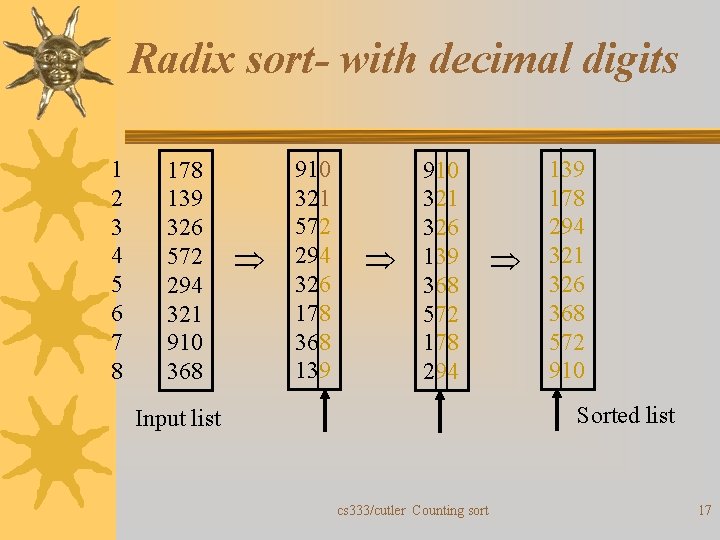
Radix sort ¬ Main idea – Break key into “digit” representation key = id, id-1, …, i 2, i 1 – "digit" can be a number in any base, a character, etc ¬ Radix sort: for i= 1 to d sort “digit” i using a stable sort ¬ Analysis : (d (stable sort time)) where d is the number of “digit”s cs 333/cutler Counting sort 15

Radix sort ¬Which stable sort? – Since the range of values of a digit is small the best stable sort to use is Counting Sort. – When counting sort is used the time complexity is (d (n +k )) where k is the range of a "digit". • When k O(n), (d n) cs 333/cutler Counting sort 16

Radix sort- with decimal digits 1 2 3 4 5 6 7 8 178 139 326 572 294 321 910 368 910 321 572 294 326 178 368 139 910 321 326 139 368 572 178 294 139 178 294 321 326 368 572 910 Sorted list Input list cs 333/cutler Counting sort 17

Lemma 8. 4 ¬ Given n b-bit numbers and any positive integer r<=b, radix sort correctly sorts these numbers in ((b/r)(n + 2 r)) ¬ Proof ¬ Divide the number into b/r “digits”. ¬ Each “digit” has r bits and a range 0 to 2 r-1. ¬ Radix sort executes b/r counting sorts. ¬ Each counting sort is (n + 2 r) ¬ So the total is ((b/r)(n + 2 r)) cs 333/cutler Counting sort 18

Radix sort with unstable digit sort 1 2 17 13 Input list 13 17 17 13 Since unstable List not sorted and both keys equal to 1 cs 333/cutler Counting sort 19

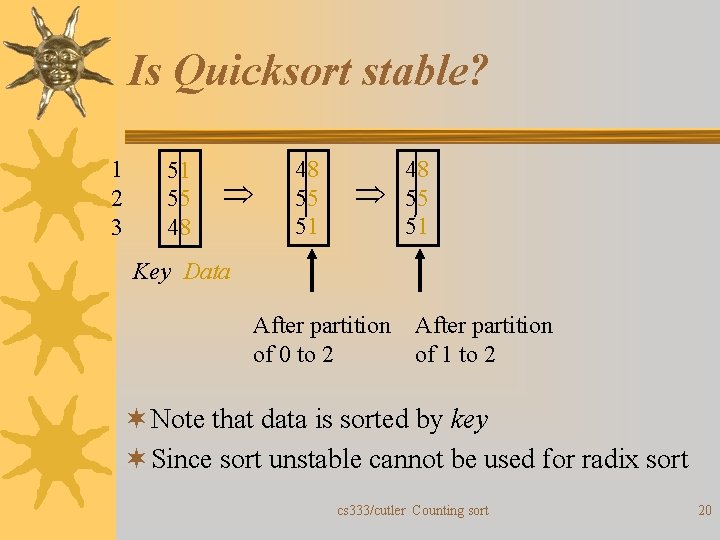
Is Quicksort stable? 1 2 3 51 55 48 48 55 51 Key Data After partition of 0 to 2 After partition of 1 to 2 ¬ Note that data is sorted by key ¬ Since sort unstable cannot be used for radix sort cs 333/cutler Counting sort 20

Is Heapsort stable? 1 51 2 55 51 Key Data 55 Complete binary tree, and max heap Heap Sorted 55 51 After swap ¬ Note that data is sorted by key ¬ Since sort unstable cannot be used for radix sort cs 333/cutler Counting sort 21