LINEAR RELATIONS AND EQUATIONS GENERAL MATHEMATICS UNIT ONE

LINEAR RELATIONS AND EQUATIONS GENERAL MATHEMATICS UNIT ONE

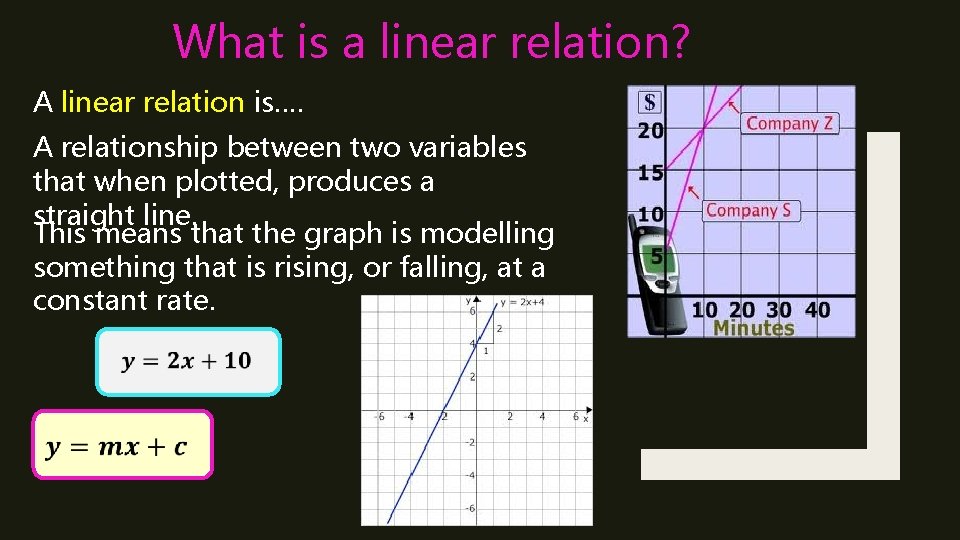
What is a linear relation? A linear relation is…. A relationship between two variables that when plotted, produces a straight line. This means that the graph is modelling something that is rising, or falling, at a constant rate.

What is a linear equation? When a linear relation is expressed as an equation, the highest power of both variables in the equation is 1. What does a linear equation look like?

What is a linear equation? When a linear relation is expressed as an equation, the highest power of both variables in the equation is 1. Which of the following are linear equations? X XX X

Number Patterns – Linear vs Non. Linear patterns have a common difference – this means the Linear numbers in the sequence increase or decrease by the same amount each time. We can look at number patterns and decide if they’re linear or non-linear, by seeing if the sequence has a common difference. Every value increases by +2 Common Difference = 2 Pattern is Linear Every value increases by x 2 No common difference Pattern is non-linear

Number Patterns – Linear vs Nona) Fill in the missing numbers. Linear in the sequences. b) Decide if the sequence is linear. Every value increases by adding 3 Common Difference = 3 Pattern is Linear Values increase by doubling the number before it. No common difference Pattern is non-linear

Number Patterns – Linear vs Nona) Fill in the missing numbers in the sequences. Linear b) Decide if the sequence is linear. Values decrease by halving each number. No common Difference Pattern is Non-Linear Values decrease by subtracting 5 from the number before it. Common Difference = -5 Pattern is Linear

Transposing Linear Equations

NOW TRY EXERCISE 1. 2 IDENTIFYING AND TRANSPOSING LINEAR EQUATIONS QUESTIONS 1, 2, 5, 6, 9, 12, 13, 14, 15

Solving Linear Equations

Solving Linear Equations

Solving Linear Equations Using the classpad “solve” function

Solving Linear Equations Using the classpad to solve equations – showing working

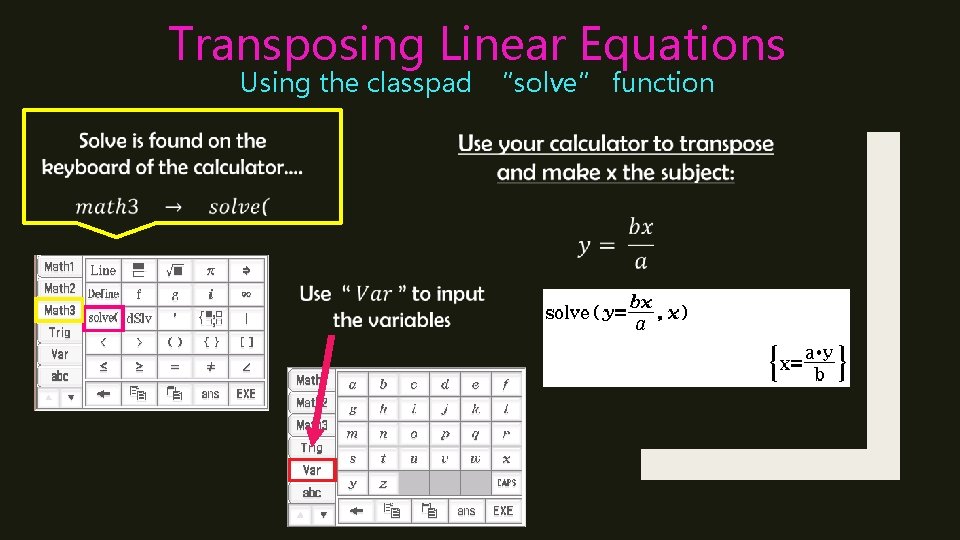
Transposing Linear Equations Using the classpad “solve” function

NOW TRY WORKSHEET ONE TRANSPOSING AND SOLVING LINEAR EQUATIONS

Substitution

Substitution

Substitution

Substitution Using the classpad to solve substitution problems “ | ” means “given that”

NOW TRY EXERCISE 1. 3 SOLVING LINEAR EQUATIONS QUESTIONS 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13 AB, 14, 17 AB, 18 AB

Developing Linear Equations from Worded Descriptions To write a worded statement as a linear equation, we must first identify the unknown and choose a pronumeral (letter) to represent it. We can then use the information given in the statement to write a linear equation in terms of the pronumeral. The linear equation can then be solved as before and we can use the result to answer the question.

Developing Linear Equations from Worded Identify the unknown and choose a pronumeral (letter) to represent it. Descriptions Use the information given in the statement to write a linear equation in terms of the pronumeral. Solve the equation and use the result to answer the question. eg 1. Pencils are sold at Officeworks in a packet of 8, costing $3. 60. Write a linear equation to represent the scenario and solve to determine the cost of one pencil. … … …

Developing Linear Equations from Worded Identify the unknown and choose a pronumeral (letter) to represent it. Descriptions Use the information given in the statement to write a linear equation in terms of the pronumeral. Solve the equation and use the result to answer the question. eg 2. Bunches of flowers are sold at the market. A bunch of 14 roses costs $21. 00. A bunch of 12 tulips costs $18. 50. Form and solve linear equations to find the cost of each individual flower. … Which is the cheaper flower? … … …

Developing Linear Equations from Worded Identify the unknown and choose a pronumeral (letter) to represent it. Descriptions Use the information given in the statement to write a linear equation in terms of the pronumeral. Solve the equation and use the result to answer the question. eg 3. One pair of sides of a rectangle are each double the size of the other pair. If the rectangle has a perimeter of 66 cm, calculate the side lengths of the rectangle. … … …

eg 4. eg 5. Developing Linear Equations from Worded 10 is added to a number and the result is 26. Descriptions Write a linear equation for this statement, then solve. 4 times a number is 32. Write a linear equation for this statement, then solve.

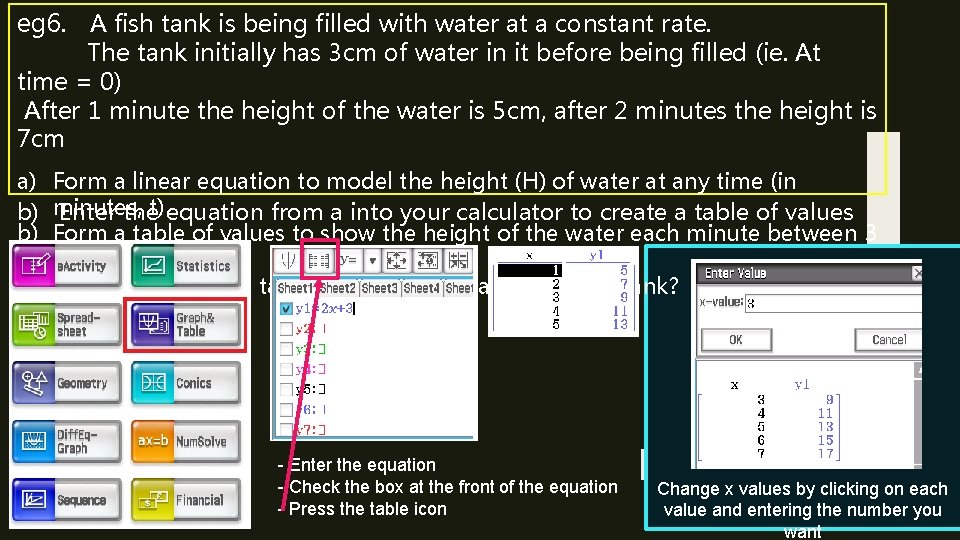
Developing Linear Equations from Worded Descriptions eg 6. A fish tank is being filled with water at a constant rate. Forming a table of values The tank initially has 3 cm of water in it before being filled (ie. At time = 0) After 1 minute the height of the water is 5 cm, after 2 minutes the height is 7 cm a) Form a linear equation to model the height (H) of water at any time (in minutes, t) b) Form a table of values to show the height of the water each minute between 3 y-intercept – 10 mins. (Initial starting point at t=0) c) If the tank is 30 cm tall, how long will it take to fill the tank? gradient (rate of change each minute)

eg 6. A fish tank is being filled with water at a constant rate. The tank initially has 3 cm of water in it before being filled (ie. At time = 0) After 1 minute the height of the water is 5 cm, after 2 minutes the height is 7 cm a) b) b) Form a linear equation to model the height (H) of water at any time (in minutes, Enter thet) equation from a into your calculator to create a table of values Form a table of values to show the height of the water each minute between 3 – 10 mins. c) If the tank is 30 cm tall, how long will it take to fill the tank? - Enter the equation - Check the box at the front of the equation - Press the table icon Change x values by clicking on each value and entering the number you want

eg 6. A fish tank is being filled with water at a constant rate. The tank initially has 3 cm of water in it before being filled (ie. At time = 0) After 1 minute the height of the water is 5 cm, after 2 minutes the height is 7 cm a) b) b) Form a linear equation to model the height (H) of water at any time (in minutes, Enter thet) equation from a into your calculator to create a table of values Form a table of values to show the height of the water each minute between 3 – 10 mins. c) If the tank is 30 cm tall, how long will it take to fill the tank?

NOW TRY EXERCISE 1. 4 SOLVING LINEAR EQUATIONS QUESTIONS 1, 2, 11, 12, 15, 16, 18, 21

Linear Relations defined recursively Linear patterns have a common difference, d – this means the numbers in the sequence increase (by adding) or decrease (by subtracting) by the same amount as we progress through the number sequence. Every value increases by +2 Common Difference = 2 Every value decreases by 5 Common Difference = -5

Linear Relations defined recursively For the following sequences, how could we find the next 4 terms in the sequence? Eg 1. Every value increases by 2. 5 Common Difference = +2. 5 Using your calculator….

Linear Relations defined recursively For the following sequences, how could we find the next 4 terms in the sequence? Eg 2. Every value decreases by 3. 5 Common Difference = - 3. 5 Using your calculator….

Linear Relations defined recursively

Linear Relations defined recursively The first term in the sequence The next term The current term The common difference Lets look at the examples we just did before and write their recurrence relation… a=4 d = 2. 5

Linear Relations defined recursively The first term in the sequence The next term The current term The common difference Given the following recurrence relation equations, write the first 5 terms in the sequence…. a=8 d=4 a = 50 d = -3. 5

Linear Relations defined recursively

Linear Relations defined recursively

NOW TRY EXERCISE 1. 4 LINEAR RELATIONS DEFINED RECURSIVELY QUESTIONS 7, 8, 9, 10, 13, 19 PLEASE USE THE DOCUMENT MRS AMSING GAVE YOU FOR THESE PROBLEMS – NOT THE TEXT BOOK

Solving Simultaneous Equations involve: • A set of two equations. • Both equations have the two variables that we need to solve for. We can solve simultaneous equations using a few different methods • Graphically – Plotting both equations on the same graph and finding where the two lines intersect (Point of Intersection). • Algebraically – Using either the: • Substitution Method • Elimination Method

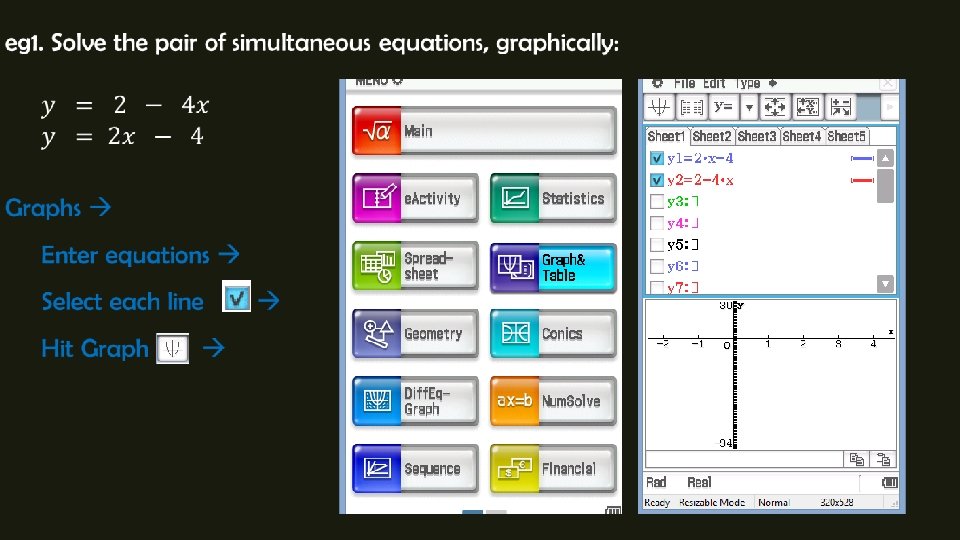
Solving Simultaneous Equations Graphically To solve these problems, we must be very accurate with our graphs, so it’s a good idea to use your calculator.

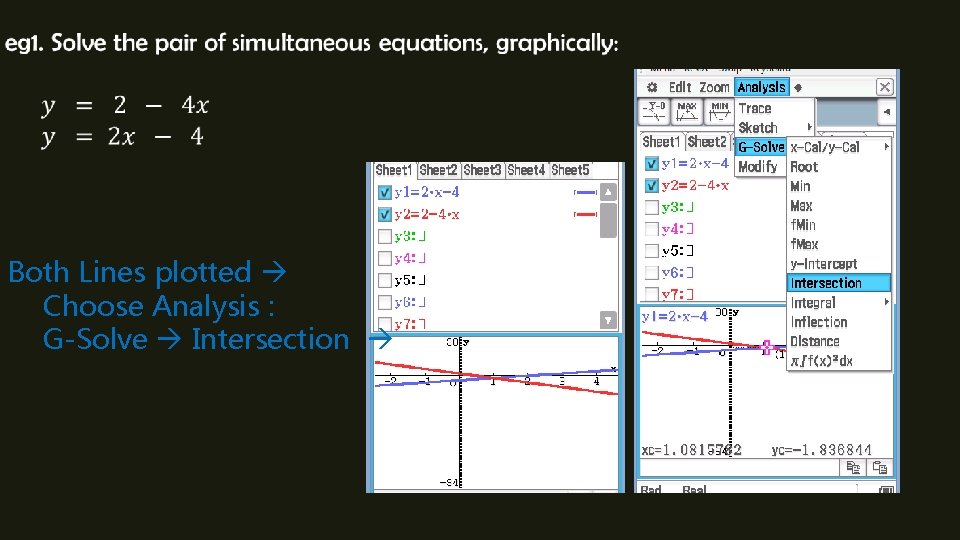
Both Lines plotted Choose Analysis : G-Solve Intersection

Solving Simultaneous Equations Graphically

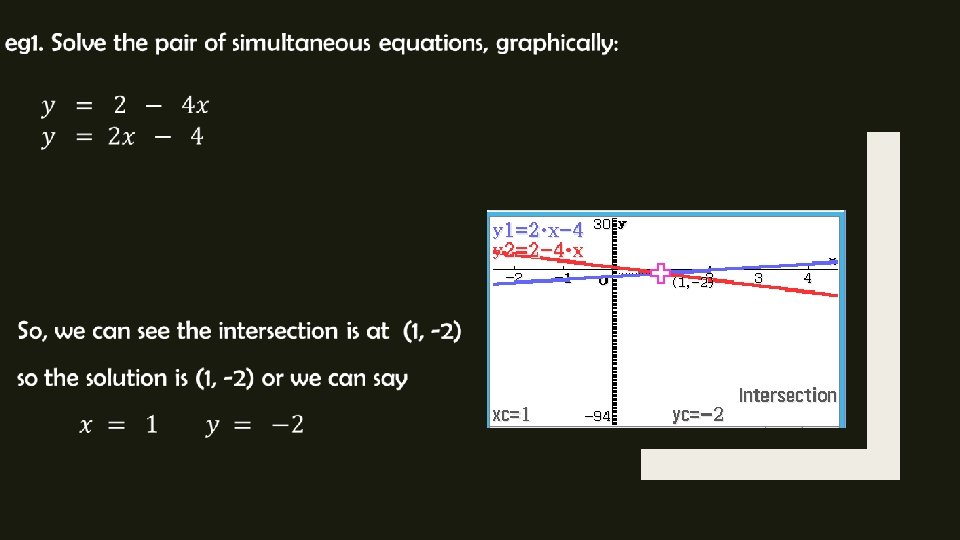
Solving Simultaneous Equations Graphically

We take the “y=” equation & substitute this into the other equation

We take the “y=” equation & substitute this into the other equation

We remove the ‘y’ and let the equations equal each other

NOW TRY SUBSTITUTION WORKSHEET

Solving Simultaneous Equations using Elimination Solving simultaneous equations using elimination requires the equations to be added or subtracted so that one of the pronumerals is eliminated or removed. Simultaneous equations that have both pronumerals on the same side are often solved using elimination. For example: 3 x + y = 5 and 4 x − y = 2 These both have x and y on the same side of the equation, so they should be solved with this method.

Solving Simultaneous Equations using Elimination SSS RULE: Signs Same Subtract The signs in front of the ‘ 3’s are not the same, so we ADD the 2 equations

Solving Simultaneous Equations using Elimination SSS RULE: Signs Same Subtract The signs in front of the ‘ 4’s are the same, so we SUBTRACT

NOW TRY ELIMINATION WORKSHEET PAGE ONE

Solving Simultaneous Equations using Elimination SSS RULE: Signs Same Subtract The signs in front of the ‘ 3’s are the same, so we SUBTRACT We multiply the whole equation by this number X 3 X 1

Solving Simultaneous Equations using Elimination SSS RULE: Signs Same Subtract The signs in front of the ‘ 6’s are the same, so we SUBTRACT We multiply the whole equation by this number X 3 X 2

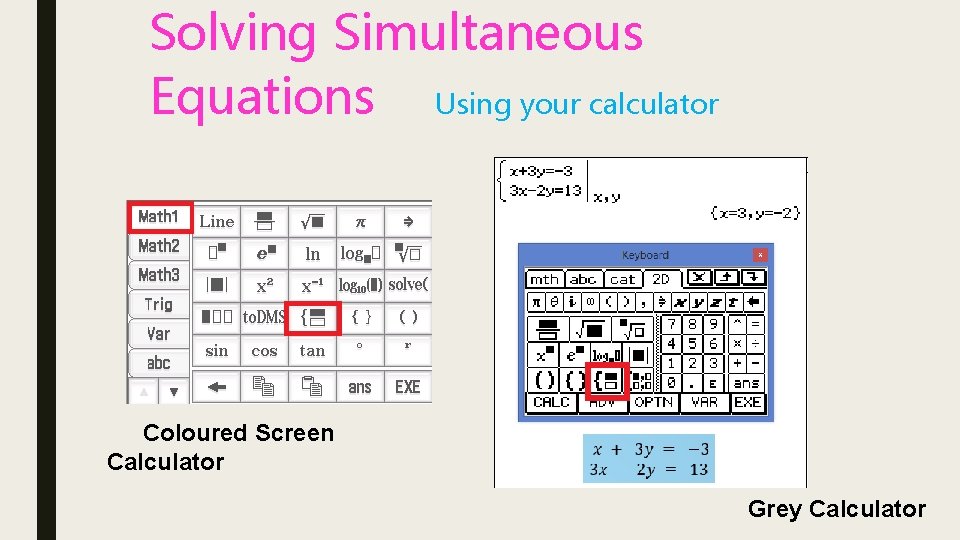
Solving Simultaneous Equations Using your calculator Coloured Screen Calculator Grey Calculator

NOW TRY ELIMINATION WORKSHEET PAGE TWO THEN TRY EXERCISE 1. 5

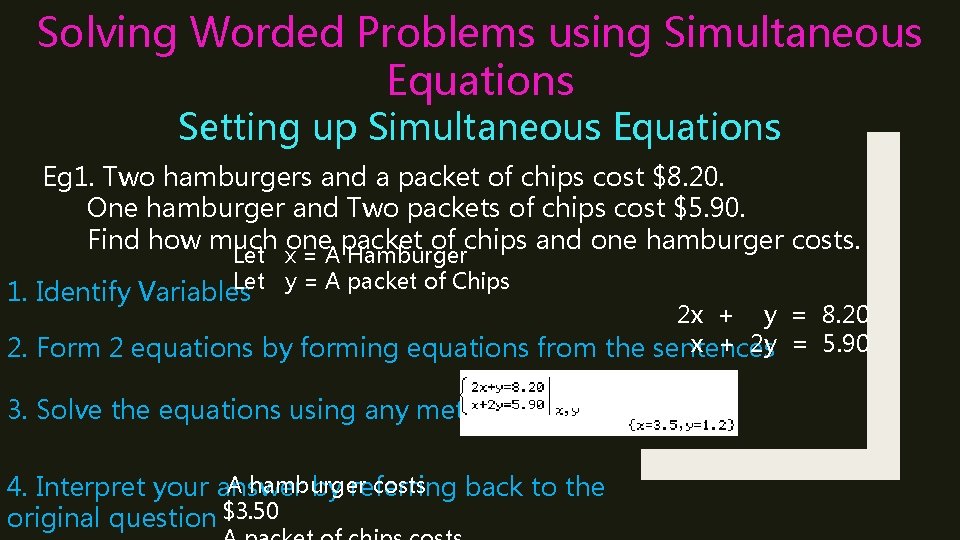
Solving Worded Problems using Simultaneous Equations Setting up Simultaneous Equations Eg 1. Two hamburgers and a packet of chips cost $8. 20. One hamburger and Two packets of chips cost $5. 90. Find how much one packet of chips and one hamburger costs. Let x = A Hamburger Let y = A packet of Chips 1. Identify Variables 2 x + y = 8. 20 x + 2 y = 5. 90 2. Form 2 equations by forming equations from the sentences 3. Solve the equations using any method A hamburger costs 4. Interpret your answer by referring back to the original question $3. 50

Setting up simultaneous equations Eg 2. The total number of adult and children watching a movie at cinema is 120. The ticket price for an adult is $18, a child is $14. The total takings for this screening was $1860. Form simultaneous equations to represent this and solve to find how many adults and Let a = number of children went to thisadults screening. Let c = number of 1. Identify Variables children 2. Form 2 equations by forming equations from the sentences 3. Solve the equations 4. Interpret your answer by referring back to the original question 45 Adults, 75 Children attended

Breakeven Points In the sales world, a breakeven point is a point where the costs = the selling price. Eg. A jeweller makes bracelets which she sells for $25 each. Her setup costs are the purchase of tools for $90 and materials for $10 per bracelet. Her costs can be represented by Her revenue (the money she takes from sales) can be represented by The break-even point is the number of bracelets that need to be sold to cover all costs. To find the break-even point, Cost and Revenue equations are solved simultaneously.

Breakeven Points How many bracelets does she need to sell to breakeven? 1. Write the equations: costs: 2. Let Cost = Revenue revenue: and solve: 3. Substitute the value into either equation & determine the value of both R and C. 4. Interpret your answer: The seller breaks even when she sells 6 bracelets, covering production costs of $150.

Breakeven Points Determine the profit or loss, in dollars, for the following bracelet orders… a) 5 bracelets costs: a) 5 Bracelets b) 30 bracelets revenue: P/L = Revenue – Cost = 125 – 140 = -15 Loss of $15 b) 30 Bracelets P/L = Revenue – Cost = 750 – 390 = $360 Profit of $360

NOW TRY EXERCISE 1. 6 Q 1, 2, 5, 6, 8, 9, 11, 12, 15