Linear Regression with Correlations Coefficient WarmUp 2 a

Linear Regression, with Correlations Coefficient

Warm-Up #2 a) Complete the missing values in the two way table. b) What is the sample space? c) How many people prefer vanilla? d) What percent of the people polled are children? ** Bonus e) Given that a person selected is an adult, what is the probability they prefer vanilla?

Essential Question #2 �How can we represent linear data using an equation and how do we know what type of correlation the data has?

Correlation �Correlation describes the relationship between two variables. �EX: How much you study verse how well you do on a test. We can say that these two variables have a relationship, therefore they are correlated.

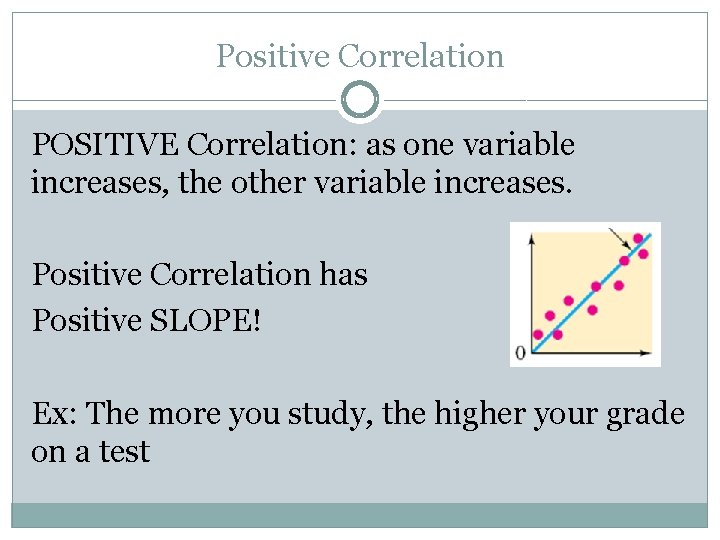
Positive Correlation POSITIVE Correlation: as one variable increases, the other variable increases. Positive Correlation has Positive SLOPE! Ex: The more you study, the higher your grade on a test

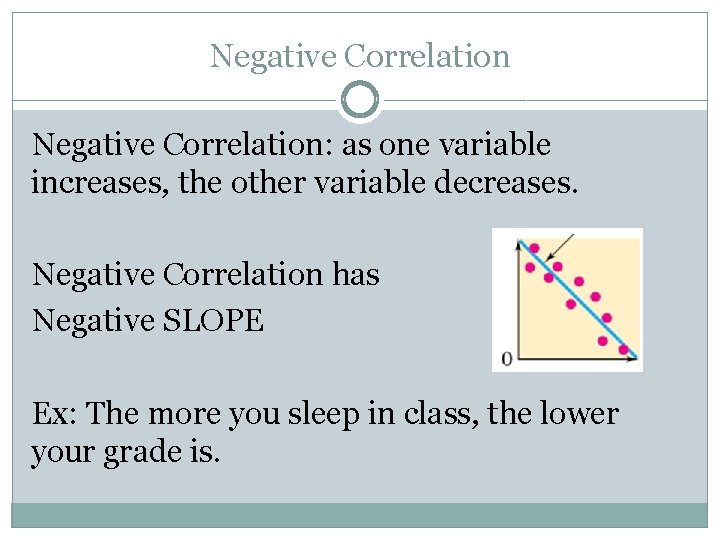
Negative Correlation: as one variable increases, the other variable decreases. Negative Correlation has Negative SLOPE Ex: The more you sleep in class, the lower your grade is.

No Correlation: When two variables are not related at all. Ex: How tall you are, and how high your grade is in English class.

Correlation Describe the following as POSITIVE, NEGATIVE or NO Correlation. 1. Hours you work, how much you get paid 2. Money you spend, Money in your savings 3. Amount of Music you listen to, How much you eat.

Correlation Coefficient: (r) is a number that tells how well a line of best fit, fits the data. - Closer to 1 or -1, the stronger the relationship - If r is close to 1, then positive correlation -If r is close to -1, then negative correlation -If r is closer to 0, then no correlation R only applies for LINEAR MODELS!!!!

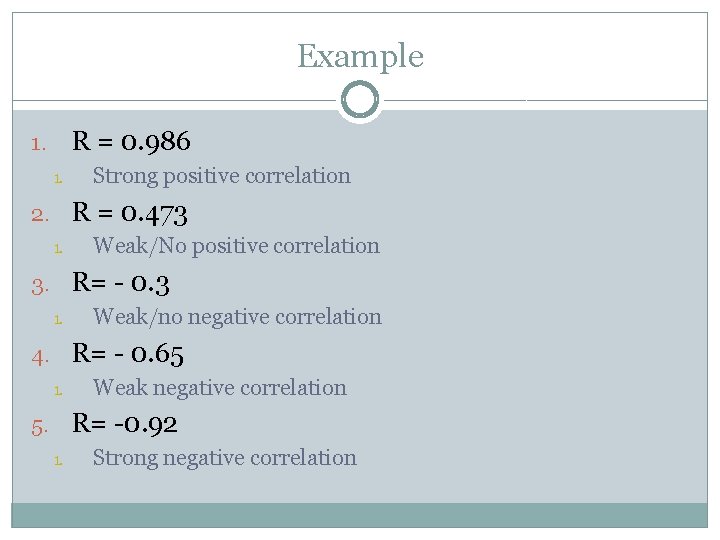
Example R = 0. 986 1. 1. Strong positive correlation 2. R = 0. 473 1. Weak/No positive correlation 3. R= - 0. 3 1. Weak/no negative correlation 4. R= - 0. 65 1. Weak negative correlation 5. R= -0. 92 1. Strong negative correlation

Turning on Correlation Coefficient Your calculator will give your Correlation Coefficient! Calculator commands: 2 nd Zero Diagnostic. On Enter

RECALL: Linear Regression To enter the data: STAT EDIT L 1 is independent variable; L 2 is dependent variable Calculator Steps: STAT CALC 4: Lin. Reg

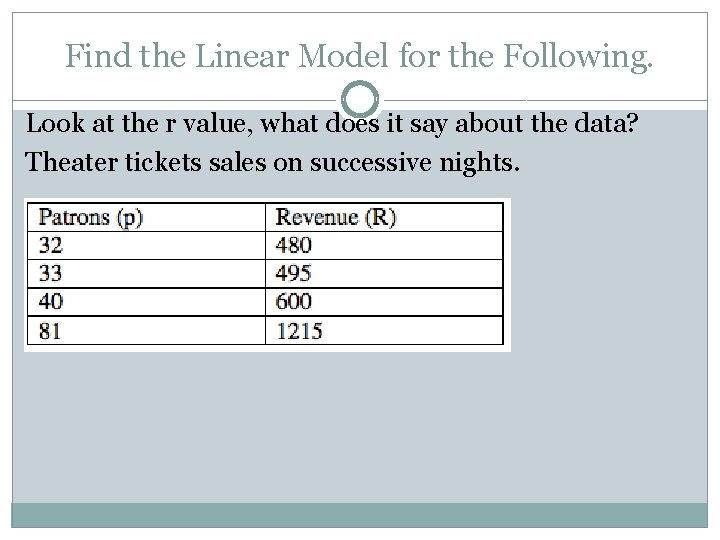
Find the Linear Model for the Following. �

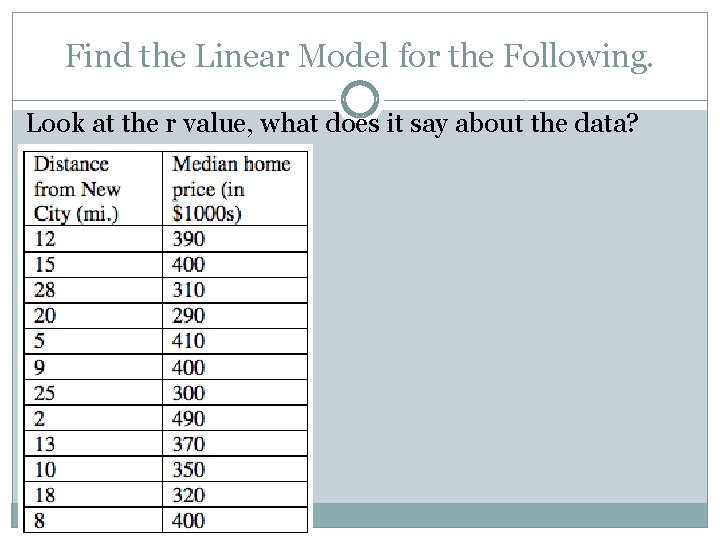
Find the Linear Model for the Following. � Look at the r value, what does it say about the data?

Find the Linear Model for the Following. Look at the r value, what does it say about the data?

Find the Linear Model for the Following. Look at the r value, what does it say about the data? Theater tickets sales on successive nights.