Linear Regression Two Variable Model Shaun Bray Math

Linear Regression: Two Variable Model Shaun Bray Math 480 April 24, 2013 The

Goal for Today: ▪ What is regression? ▪ Population Regression Function (PRF) ▪ Sample Regression Function (SRF) ▪ The Method of Ordinary Least Squares ▪ How to interpret regression function

What is Regression Analysis? ▪ Concerned with the study of the relationship between one variable (dependent) and one or more other variables (independent). ▪ Examples: – Quantity demanded of a commodity in terms of the price of the commodity, income of the consumer, and prices of competing commodities. – Sales of a product related to advertising expenditure incurred.

Regression analysis may have one of the following objectives: ▪ To estimate the mean value of the dependent variable, given the values of the independent variables. ▪ To test hypotheses about the nature of dependence. ▪ Predict the mean value of the dependent variable, given the value(s) of the independent variables(s) beyond the sample range. ▪ A combination of one or more of these objectives.

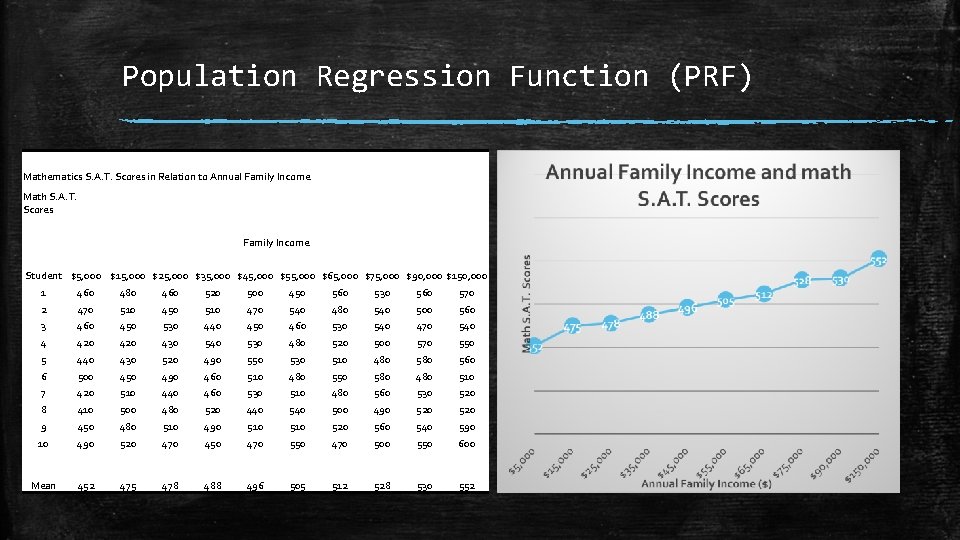
Population Regression Function (PRF) Mathematics S. A. T. Scores in Relation to Annual Family Income Math S. A. T. Scores Family Income Student $5, 000 $15, 000 $25, 000 $35, 000 $45, 000 $55, 000 $65, 000 $75, 000 $90, 000 $150, 000 1 460 480 460 520 500 450 560 530 560 570 2 470 510 450 510 470 540 480 540 500 560 3 460 450 530 440 450 460 530 540 470 540 4 420 430 540 530 480 520 500 570 550 5 440 430 520 490 550 530 510 480 560 6 500 450 490 460 510 480 550 580 480 510 7 420 510 440 460 530 510 480 560 530 520 8 410 500 480 520 440 500 490 520 9 450 480 510 490 510 520 560 540 590 10 490 520 470 450 470 500 550 600 Mean 452 475 478 488 496 505 512 528 530 552

Population Regression Function (PRF) ▪

Sample Regression Function (SRF) ▪ The PRF is relatively easy to find if we have data of an entire population. ▪ In practice, this is hardly ever the case, so we often look for a sample of a population. ▪ The task here is to estimate the PRF on the basis of the sample information.

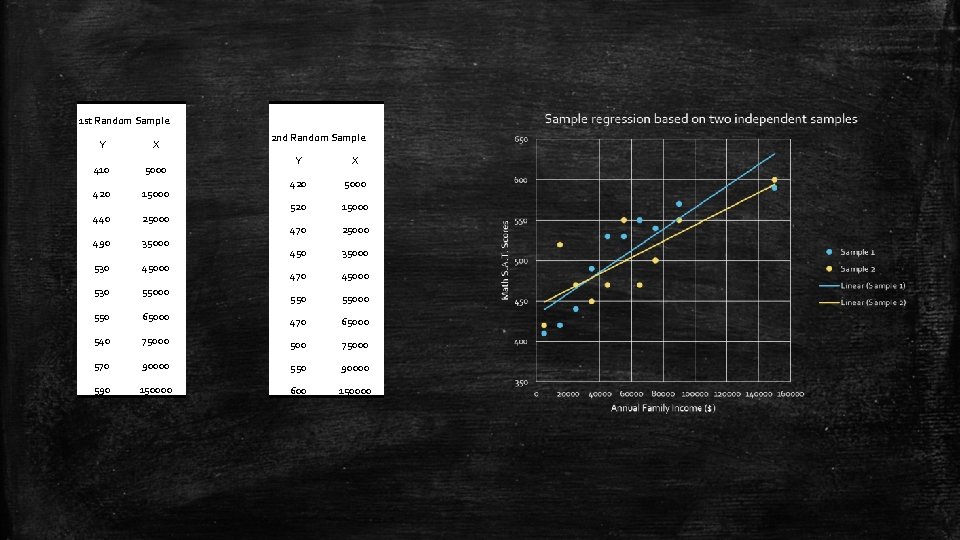
1 st Random Sample Y X 410 5000 420 15000 440 25000 490 35000 530 45000 530 55000 550 2 nd Random Sample Y X 420 5000 520 15000 470 25000 450 35000 470 45000 55000 65000 470 65000 540 75000 500 75000 570 90000 550 90000 590 150000 600 150000

Sample Regression Function (SRF) ▪

Method of Ordinary Least Squares ▪

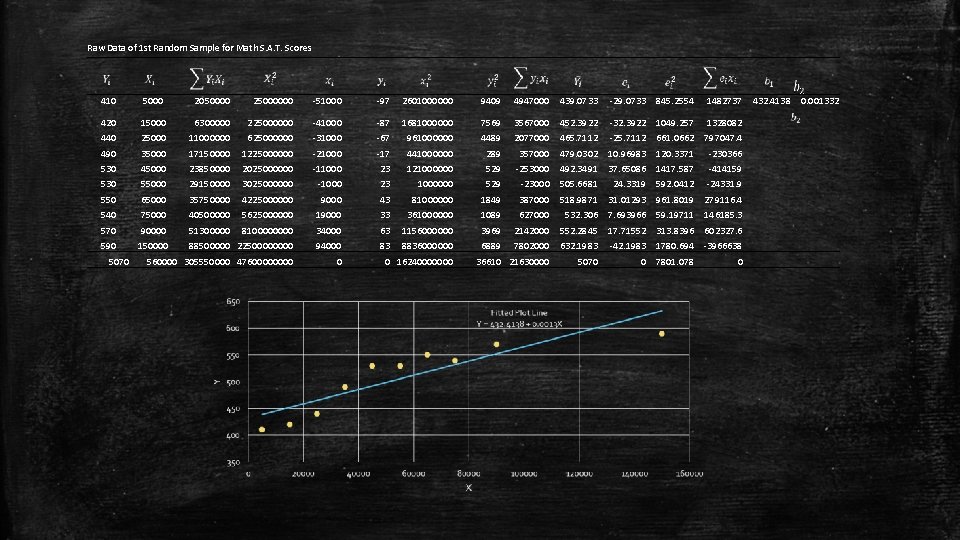
Raw Data of 1 st Random Sample for Math S. A. T. Scores 410 5000 2050000 25000000 -51000 -97 2601000000 9409 4947000 439. 0733 -29. 0733 845. 2554 1482737 420 15000 6300000 225000000 -41000 -87 1681000000 7569 3567000 452. 3922 -32. 3922 1049. 257 1328082 440 25000 11000000 625000000 -31000 -67 961000000 4489 2077000 465. 7112 -25. 7112 661. 0662 797047. 4 490 35000 17150000 1225000000 -21000 -17 441000000 289 357000 479. 0302 10. 96983 120. 3371 -230366 530 45000 23850000 2025000000 -11000 23 121000000 529 -253000 492. 3491 37. 65086 1417. 587 -414159 530 55000 29150000 3025000000 -1000 23 1000000 529 -23000 505. 6681 24. 3319 592. 0412 -24331. 9 550 65000 35750000 4225000000 9000 43 81000000 1849 387000 518. 9871 31. 01293 961. 8019 279116. 4 540 75000 40500000 5625000000 19000 33 361000000 1089 627000 532. 306 7. 693966 59. 19711 146185. 3 570 90000 51300000 810000 34000 63 1156000000 3969 2142000 552. 2845 17. 71552 313. 8396 602327. 6 590 150000 88500000 2250000 94000 83 8836000000 6889 7802000 632. 1983 -42. 1983 1780. 694 -3966638 560000 305550000 4760000 0 36610 21630000 5070 0 16240000000 0 7801. 078 0 432. 4138 0. 001332

Conclusion ▪ What is regression analysis and what are its objectives? ▪ Population and Sample Regression Functions ▪ The Method of Ordinary Least Squares