Linear Regression The relationship between two variables e

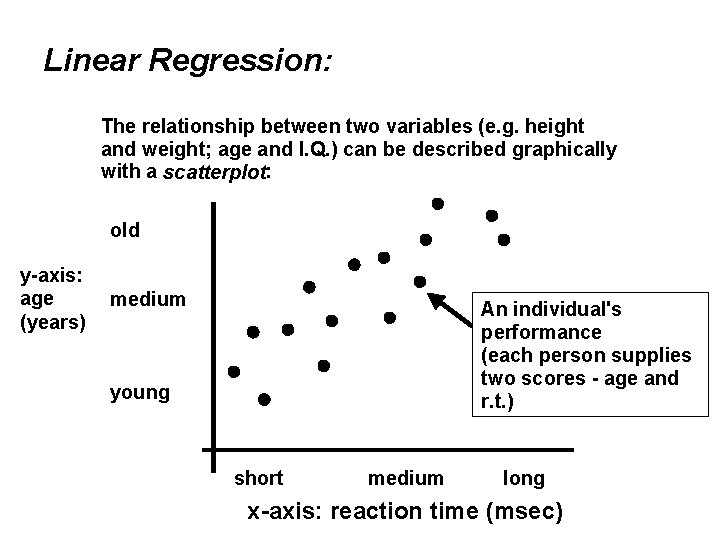
Linear Regression: The relationship between two variables (e. g. height and weight; age and I. Q. ) can be described graphically with a scatterplot: old y-axis: age (years) medium An individual's performance (each person supplies two scores - age and r. t. ) young short medium long x-axis: reaction time (msec)

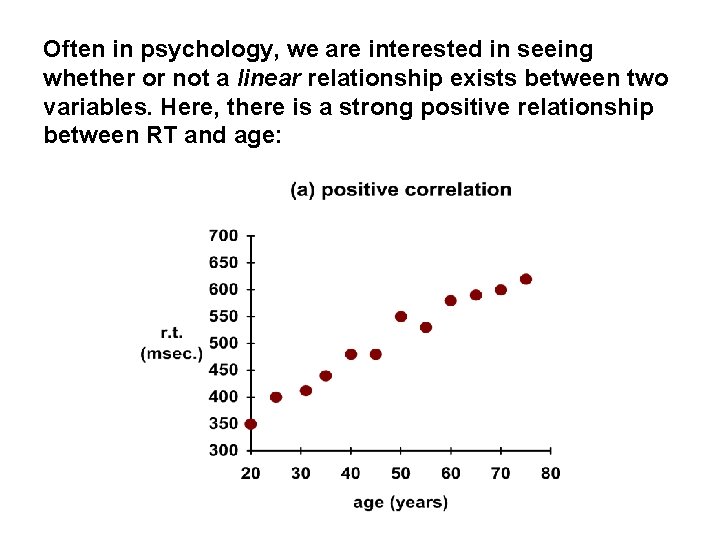
Often in psychology, we are interested in seeing whether or not a linear relationship exists between two variables. Here, there is a strong positive relationship between RT and age:

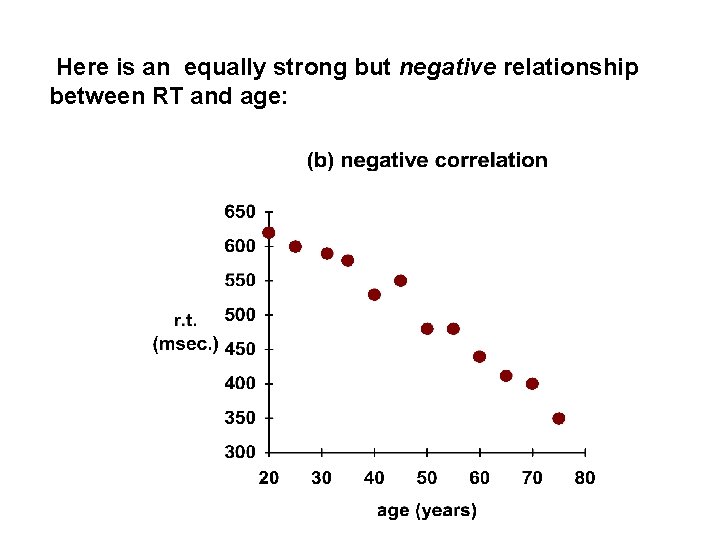
Here is an equally strong but negative relationship between RT and age:

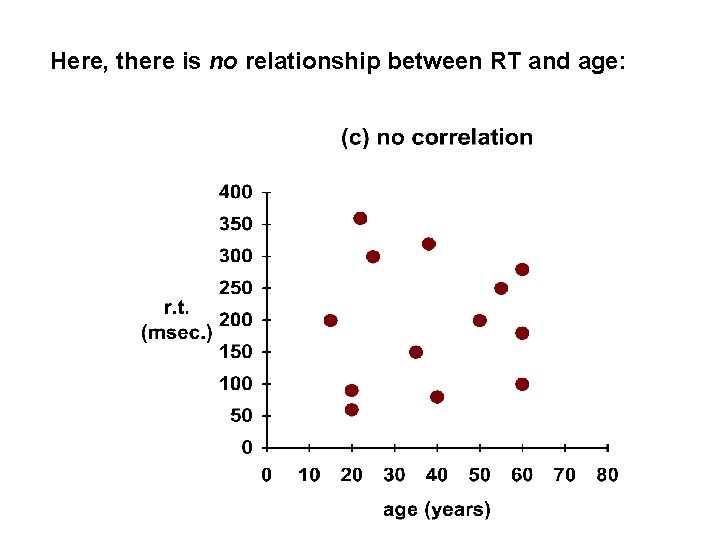
Here, there is no relationship between RT and age:

If we find a reasonably strong linear relationship between two variables, we might want to fit a straight line to the scatterplot. There are two reasons for wanting to do this: (a) for description: the line acts as a succinct description of the "idealised" relationship between our two variables, a relationship which we assume the real data reflect somewhat imperfectly. (b) for prediction: we could use the line to obtain estimates of values for one of the variables, on the basis of knowledge of the value of the other variable (e. g. if we knew a person's height, we could predict their weight).

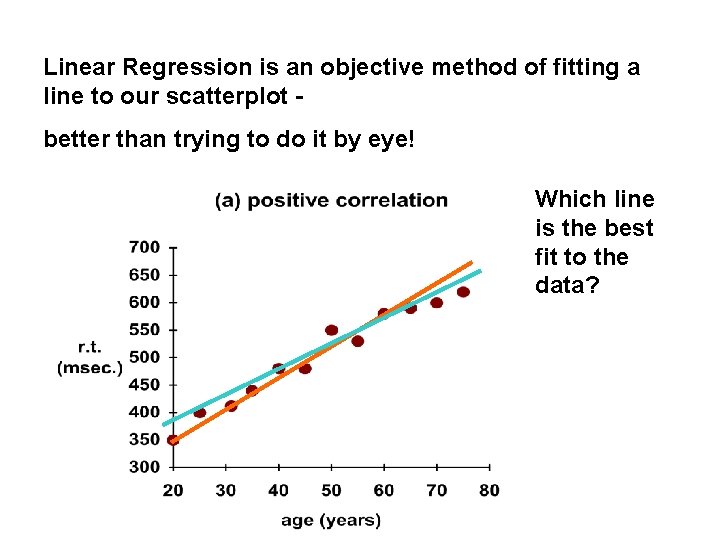
Linear Regression is an objective method of fitting a line to our scatterplot better than trying to do it by eye! Which line is the best fit to the data?

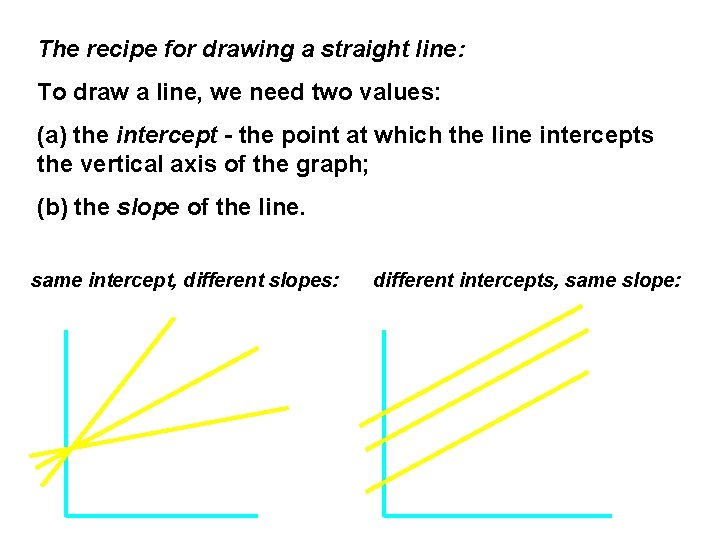
The recipe for drawing a straight line: To draw a line, we need two values: (a) the intercept - the point at which the line intercepts the vertical axis of the graph; (b) the slope of the line. same intercept, different slopes: different intercepts, same slope:

The formula for a straight line: Y = a+ b * X Y is a value on the vertical (Y) axis; a is the intercept (the point at which the line intersects the vertical axis of the graph); b is the slope of the line; X is any value on the horizontal (X) axis.

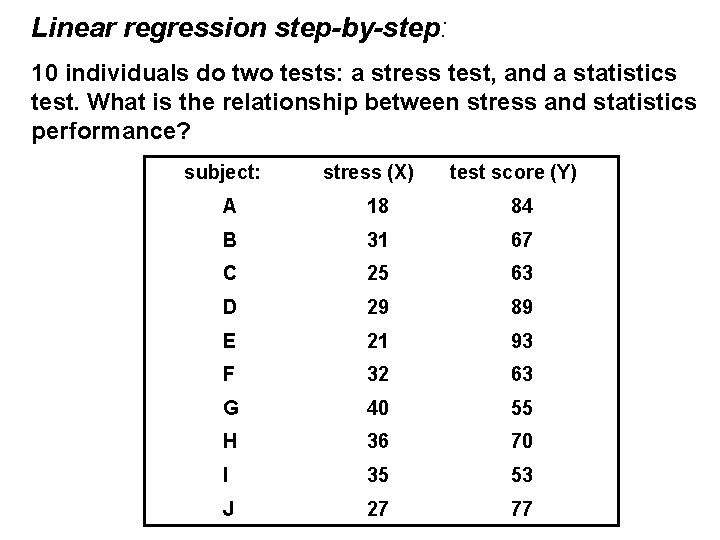
Linear regression step-by-step: 10 individuals do two tests: a stress test, and a statistics test. What is the relationship between stress and statistics performance? subject: stress (X) test score (Y) A 18 84 B 31 67 C 25 63 D 29 89 E 21 93 F 32 63 G 40 55 H 36 70 I 35 53 J 27 77

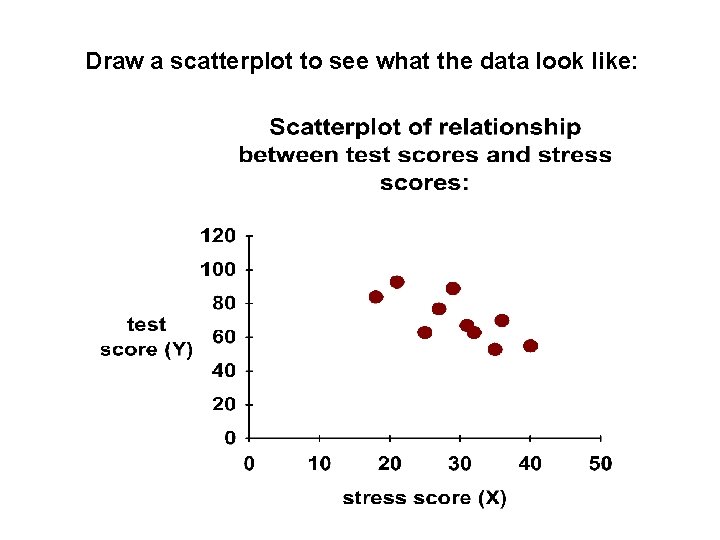
Draw a scatterplot to see what the data look like:

There is a negative relationship between stress scores and statistics scores: people who scored high on the statistics test tend to have low stress levels, and people who scored low on the statistics test tend to have high stress levels.

Calculating the regression line: We need to find "a" (the intercept) and "b" (the slope) of the line. Work out "b" first, and "a" second.

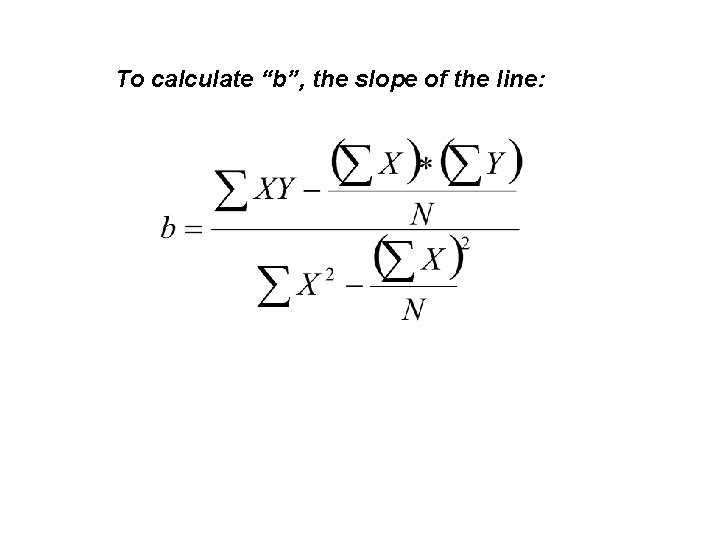
To calculate “b”, the slope of the line:

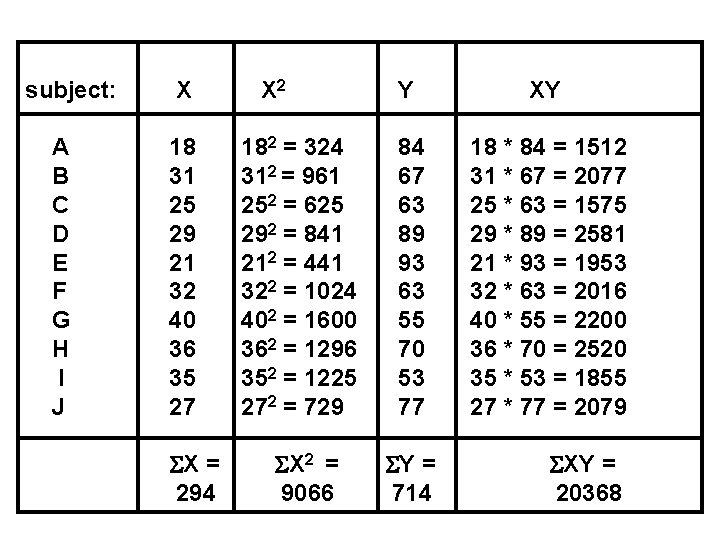
subject: A B C D E F G H I J X 18 31 25 29 21 32 40 36 35 27 X = 294 X 2 182 = 324 312 = 961 252 = 625 292 = 841 212 = 441 322 = 1024 402 = 1600 362 = 1296 352 = 1225 272 = 729 X 2 = 9066 Y XY 84 67 63 89 93 63 55 70 53 77 18 * 84 = 1512 31 * 67 = 2077 25 * 63 = 1575 29 * 89 = 2581 21 * 93 = 1953 32 * 63 = 2016 40 * 55 = 2200 36 * 70 = 2520 35 * 53 = 1855 27 * 77 = 2079 Y = 714 XY = 20368

We also need: N = the number of pairs of scores, = 10 in this case. ( X)2 = "the sum of X squared" = 294 * 294 = 86436. NB: ( X)2 means "square the sum of X"; add together all of the X values to get a total, and then square this total. X 2 means "sum the squared X values"; square each X value, and then add together these squared X values to get a total.

Working through the formula for b: = - 623. 60 422. 40 = - 1. 476

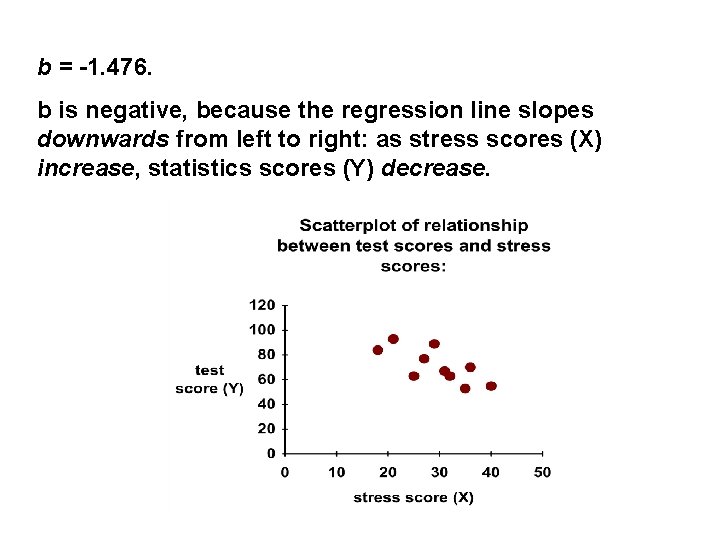
b = -1. 476. b is negative, because the regression line slopes downwards from left to right: as stress scores (X) increase, statistics scores (Y) decrease.

Now work out a: Y is the mean of the Y scores: = 71. 4. X is the mean of the X scores: = 29. 4. b = -1. 476 Therefore a = 71. 4 - (-1. 476 * 29. 4) = 114. 80.

The complete regression equation: Y' = 114. 80 + ( -1. 476 * X) To draw the line, input any three different values for X, in order to get associated values for Y'. For X = 10, Y' = 114. 80 + (-1. 476 * 10) = 100. 04. For X = 30, Y' = 114. 80 + (-1. 476 * 30) = 70. 52. For X = 50, Y' = 114. 80 + (-1. 476 * 50) = 41. 00.

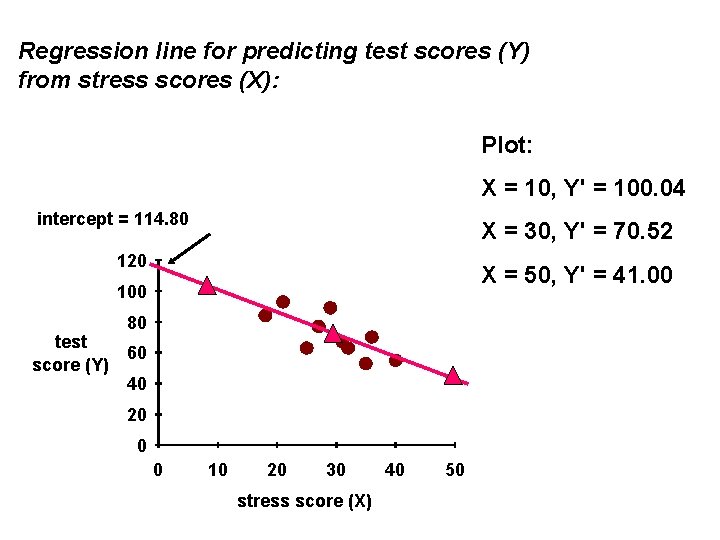
Regression line for predicting test scores (Y) from stress scores (X): Plot: X = 10, Y' = 100. 04 intercept = 114. 80 X = 30, Y' = 70. 52 120 X = 50, Y' = 41. 00 100 80 test 60 score (Y) 40 20 0 0 10 20 30 stress score (X) 40 50

This is the regression line for predicting test score on the basis of knowledge of a person's stress score; this is the "regression of Y on X". To predict stress score on the basis of knowledge of test score (the "regression of X on Y"), we can't use this regression line! To predict Y from X requires a line that minimises the deviations of the predicted Y's from actual Y's. To predict X from Y requires a line that minimises the deviations of the predicted X's from actual X's - a different task! Solution: to calculate regression of X on Y, swap the column labels (so that the "X" values are now the "Y" values, and vice versa); and re-do the calculations.

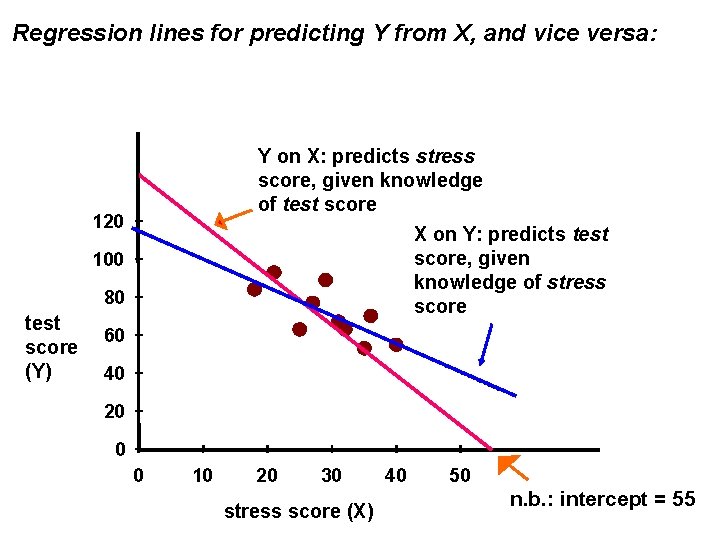
Regression lines for predicting Y from X, and vice versa: Y on X: predicts stress score, given knowledge of test score X on Y: predicts test score, given knowledge of stress score 120 100 80 test score (Y) 60 40 20 0 0 10 20 30 stress score (X) 40 50 n. b. : intercept = 55