Linear Regression and Correlation Analysis Scatter Diagrams A

Linear Regression and Correlation Analysis

Scatter Diagrams A scatter plot is a graph that may be used to represent the relationship between two variables. Also referred to as a scatter diagram

Dependent and Independent Variables A dependent variable is the variable to be predicted or explained in a regression model. This variable is assumed to be functionally related to the independent variable.

Dependent and Independent Variables An independent variable is the variable related to the dependent variable in a regression equation. The independent variable is used in a regression model to estimate the value of the dependent variable.

Two Variable Relationships (Figure 11 -1) Y X (a) Linear

Two Variable Relationships (Figure 11 -1) Y X (b) Linear

Two Variable Relationships (Figure 11 -1) Y X (c) Curvilinear

Two Variable Relationships (Figure 11 -1) Y X (d) Curvilinear

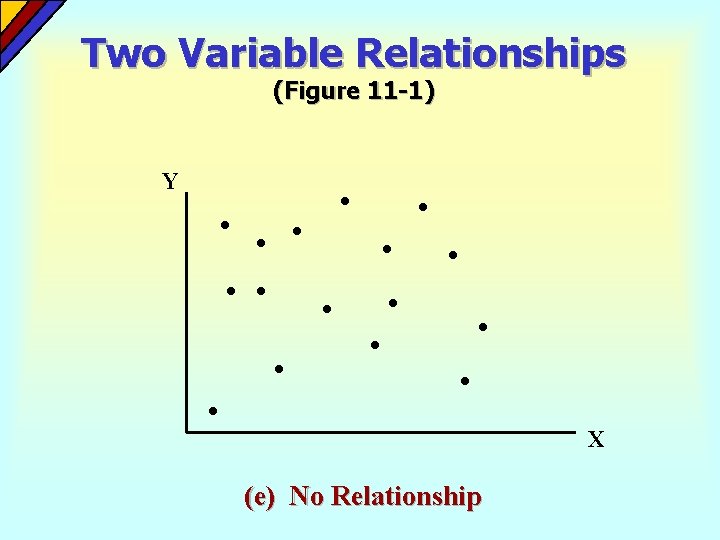
Two Variable Relationships (Figure 11 -1) Y X (e) No Relationship

Correlation The correlation coefficient is a quantitative measure of the strength of the linear relationship between two variables. The correlation ranges from + 1. 0 to - 1. 0. A correlation of 1. 0 indicates a perfect linear relationship, whereas a correlation of 0 indicates no linear relationship.

Correlation SAMPLE CORRELATION COEFFICIENT where: r = Sample correlation coefficient n = Sample size x = Value of the independent variable y = Value of the dependent variable

Correlation SAMPLE CORRELATION COEFFICIENT or the algebraic equivalent:

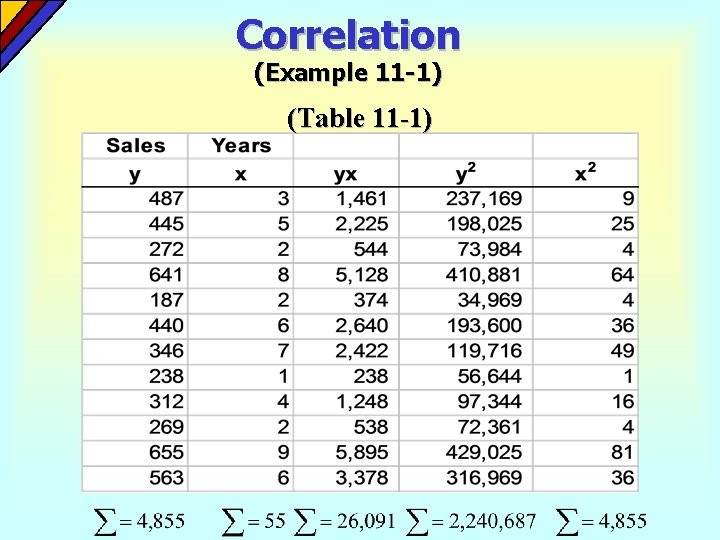
Correlation (Example 11 -1) (Table 11 -1)

Correlation (Example 11 -1)

Correlation TEST STATISTIC FOR CORRELATION where: t = Number of standard deviations r is from 0 r = Simple correlation coefficient n = Sample size

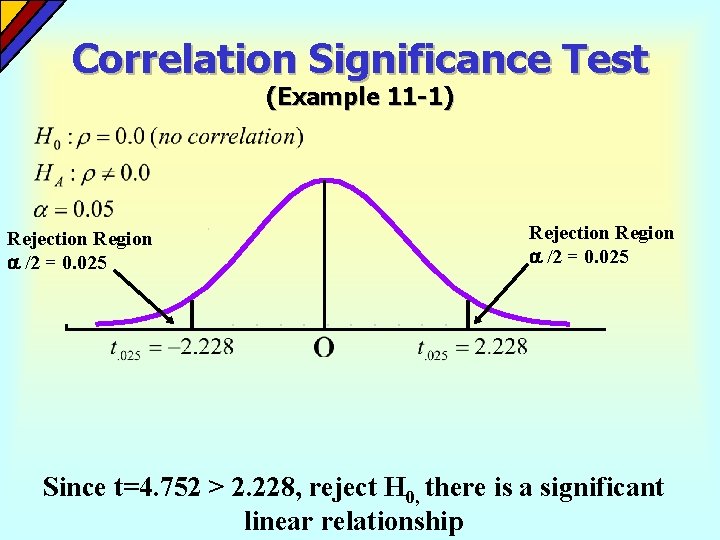
Correlation Significance Test (Example 11 -1) Rejection Region /2 = 0. 025 Since t=4. 752 > 2. 228, reject H 0, there is a significant linear relationship

Simple Linear Regression Analysis Simple linear regression analysis analyzes the linear relationship that exists between a dependent variable and a single independent variable.

Simple Linear Regression Analysis SIMPLE LINEAR REGRESSION MODEL (POPULATION MODEL) where: y = Value of the dependent variable x = Value of the independent variable = Population’s y-intercept = Slope of the population regression line = Error term, or residual

Simple Linear Regression Analysis The simple linear regression model has four assumptions: 4 Individual values of the error terms, i, are statistically independent of one another. 4 The distribution of all possible values of is normal. 4 The distributions of possible i values have equal variances for all value of x. 4 The means of the dependent variable, for all specified values of the independent variable, y, can be connected by a straight line called the population regression model.

Simple Linear Regression Analysis REGRESSION COEFFICIENTS In the simple regression model, there are two coefficients: the intercept and the slope.

Simple Linear Regression Analysis The interpretation of the regression slope coefficient is that is gives the average change in the dependent variable for a unit increase in the independent variable. The slope coefficient may be positive or negative, depending on the relationship between the two variables.

Simple Linear Regression Analysis The least squares criterion is used for determining a regression line that minimizes the sum of squared residuals.

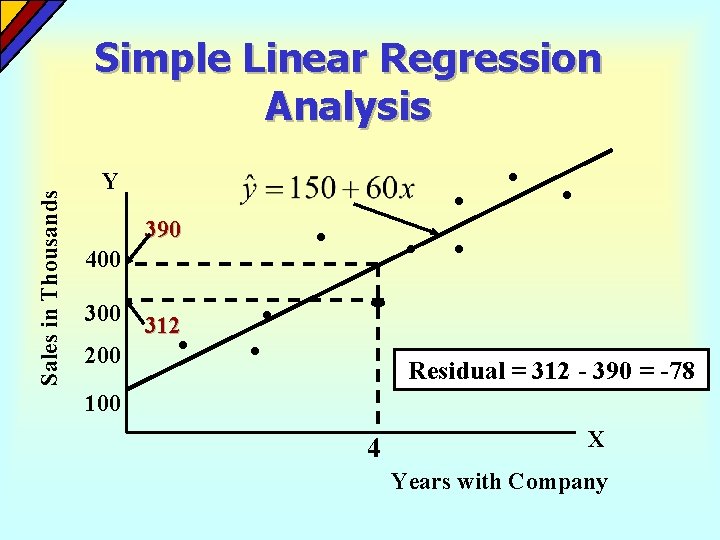
Simple Linear Regression Analysis A residual is the difference between the actual value of the dependent variable and the value predicted by the regression model.

Sales in Thousands Simple Linear Regression Analysis Y 390 400 312 200 Residual = 312 - 390 = -78 100 4 X Years with Company

Simple Linear Regression Analysis ESTIMATED REGRESSION MODEL (SAMPLE MODEL) where: = Estimated, or predicted, y value b 0 = Unbiased estimate of the regression intercept b 1 = Unbiased estimate of the regression slope x = Value of the independent variable

Simple Linear Regression Analysis LEAST SQUARES EQUATIONS algebraic equivalent: and

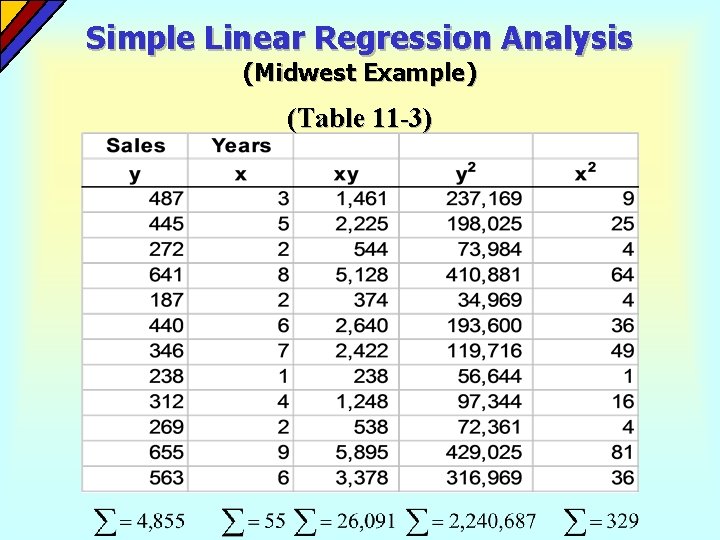
Simple Linear Regression Analysis (Midwest Example) (Table 11 -3)

Simple Linear Regression Analysis (Table 11 -3) The least squares regression line is:

Least Squares Regression Properties 4 The sum of the residuals from the least squares regression line is 0. 4 The sum of the squared residuals is a minimum. 4 The simple regression line always passes through the mean of the y variable and the mean of the x variable. 4 The least squares coefficients are unbiased estimates of 0 and 1.

Simple Linear Regression Analysis SUMS OF SQUARES

Simple Linear Regression Analysis TOTAL SUM OF SQUARES where: TSS = Total sum of squares n = Sample size y = Values of the dependent variable = Average value of the dependent variable

Simple Linear Regression Analysis SUM OF RESIDUALS SUM OF SQUARED RESIDUALS

Simple Linear Regression Analysis SUM OF SQUARES ERROR (RESIDUALS) where: SSE = Sum of squares error n = Sample size y = Values of the dependent variable = Estimated value for the average of y for the given x value

Simple Linear Regression Analysis SUM OF SQUARED ERRORS

Simple Linear Regression Analysis SUM OF SQUARES REGRESSION where: SSR = Sum of squares regression = Average value of the dependent variable y = Values of the dependent variable = Estimated value for the average of y for the given x value

Simple Linear Regression Analysis The coefficient of determination is the portion of the total variation in the dependent variable that is explained by its relationship with the independent variable. The coefficient of determination is also called R-squared and is denoted as R 2.

Simple Linear Regression Analysis COEFFICIENT OF DETERMINATION (R 2)

Simple Linear Regression Analysis (Midwest Example) COEFFICIENT OF DETERMINATION (R 2) 69. 31% of the variation in the sales data for this sample can be explained by the linear relationship between sales and years of experience.

Simple Linear Regression Analysis COEFFICIENT OF DETERMINATION SINGLE INDEPENDENT VARIABLE CASE where: R 2 = Coefficient of determination r = Sample correlation coefficient

Simple Linear Regression Analysis STANDARD DEVIATION OF THE REGRESSION SLOPE COEFFICIENT (POPULATION) where: = Standard deviation of the regression slope (Called the standard error of the slope) = Population standard error of the estimate

Simple Linear Regression Analysis ESTIMATOR FOR THE STANDARD ERROR OF THE ESTIMATE where: SSE = Sum of squares error n = Sample size k = number of independent variables in the model

Simple Linear Regression Analysis ESTIMATOR FOR THE STANDARD DEVIATION OF THE REGRESSION SLOPE where: = Estimate of the standard error of the least squares slope = Sample standard error of the estimate

Simple Linear Regression Analysis TEST STATISTIC FOR TEST OF SIGNIFICANCE OF THE REGRESSION SLOPE where: b 1 = Sample regression slope coefficient 1 = Hypothesized slope sb 1 = Estimator of the standard error of the slope

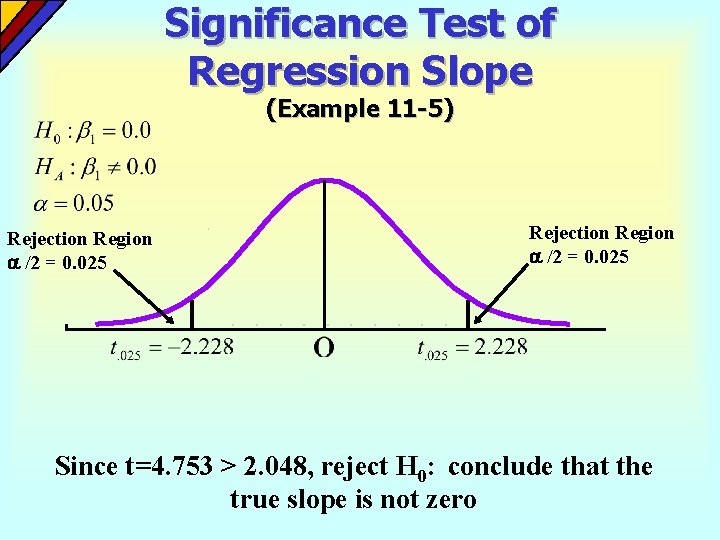
Significance Test of Regression Slope (Example 11 -5) Rejection Region /2 = 0. 025 Since t=4. 753 > 2. 048, reject H 0: conclude that the true slope is not zero

Simple Linear Regression Analysis MEAN SQUARE REGRESSION where: SSR = Sum of squares regression k = Number of independent variables in the model

Simple Linear Regression Analysis MEAN SQUARE ERROR where: SSE = Sum of squares error n = Sample size k = Number of independent variables in the model

Significance Test (Example 11 -6) Rejection Region = 0. 05 Since F= 22. 59 > 4. 96, reject H 0: conclude that the regression model explains a significant amount of the variation in the dependent variable

Simple Regression Steps ¬Develop a scatter plot of y and x. You are looking for a linear relationship between the two variables. Calculate the least squares regression line for the sample data. ®Calculate the correlation coefficient and the simple coefficient of determination, R 2. ¯Conduct one of the significance tests.

Simple Linear Regression Analysis CONFIDENCE INTERVAL ESTIMATE FOR THE REGRESSION SLOPE or equivalently: where: sb 1 = Standard error of the regression slope coefficient s = Standard error of the estimate

Simple Linear Regression Analysis CONFIDENCE INTERVAL FOR where: = Point estimate of the dependent variable t = Critical value with n - 2 d. f. s = Standard error of the estimate n = Sample size xp = Specific value of the independent variable = Mean of independent variable observations

Simple Linear Regression Analysis PREDICTION INTERVAL FOR

Residual Analysis Before using a regression model for description or prediction, you should do a check to see if the assumptions concerning the normal distribution and constant variance of the error terms have been satisfied. One way to do this is through the use of residual plots