Linear ProgrammingBellwork Algebra 2 Multiple Choice What values

Linear Programming-Bellwork Algebra 2 Multiple Choice: What values of x and y minimize P for the objective function P = 3 x + 2 y? A. (2, 0) B. ( 2, 6) C. (4, 3) D. (4, 4)

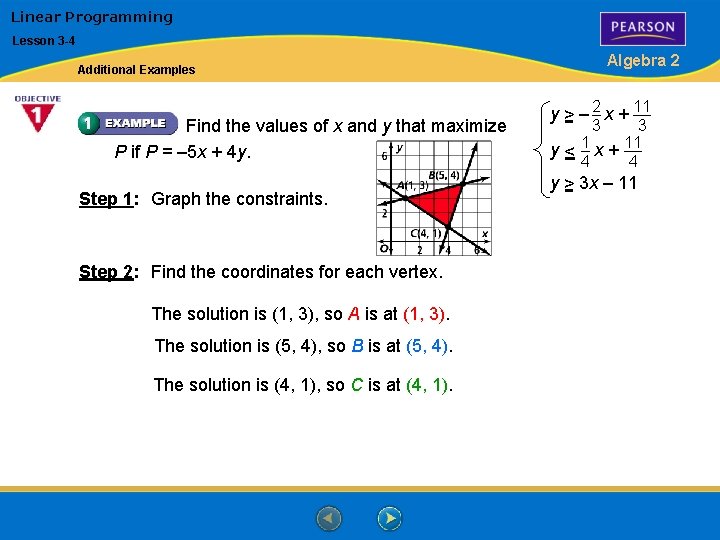
Linear Programming Lesson 3 -4 Algebra 2 Additional Examples Find the values of x and y that maximize P if P = – 5 x + 4 y. Step 1: Graph the constraints. Step 2: Find the coordinates for each vertex. The solution is (1, 3), so A is at (1, 3). The solution is (5, 4), so B is at (5, 4). The solution is (4, 1), so C is at (4, 1). y > – 2 x + 11 3 3 y < 1 x + 11 4 4 y > 3 x – 11

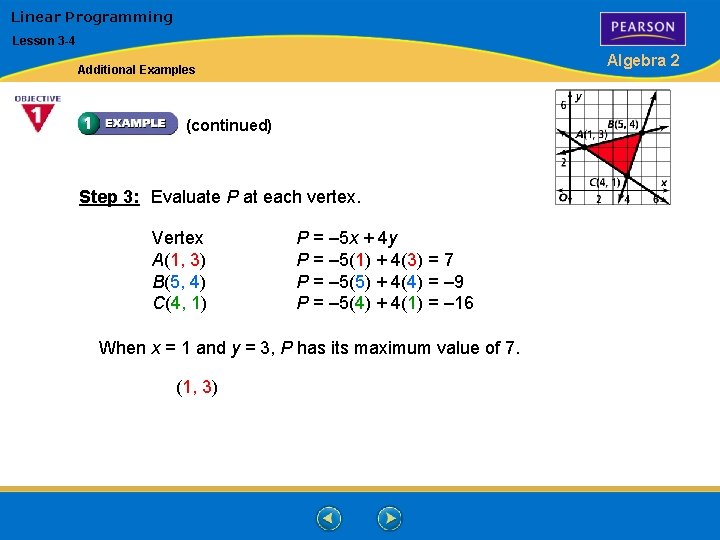
Linear Programming Lesson 3 -4 Algebra 2 Additional Examples (continued) Step 3: Evaluate P at each vertex. Vertex A(1, 3) B(5, 4) C(4, 1) P = – 5 x + 4 y P = – 5(1) + 4(3) = 7 P = – 5(5) + 4(4) = – 9 P = – 5(4) + 4(1) = – 16 When x = 1 and y = 3, P has its maximum value of 7. (1, 3)

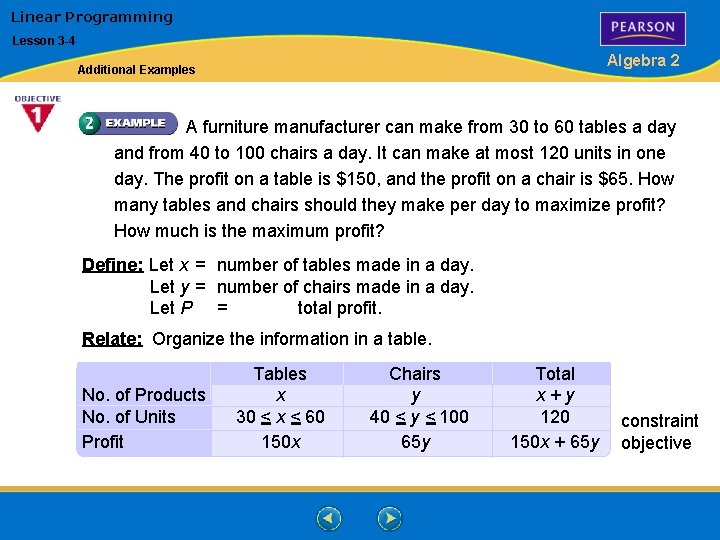
Linear Programming Lesson 3 -4 Algebra 2 Additional Examples A furniture manufacturer can make from 30 to 60 tables a day and from 40 to 100 chairs a day. It can make at most 120 units in one day. The profit on a table is $150, and the profit on a chair is $65. How many tables and chairs should they make per day to maximize profit? How much is the maximum profit? Define: Let x = number of tables made in a day. Let y = number of chairs made in a day. Let P = total profit. Relate: Organize the information in a table. No. of Products No. of Units Profit Tables x 30 < x < 60 150 x Chairs y 40 < y < 100 65 y Total x+y 120 150 x + 65 y constraint objective

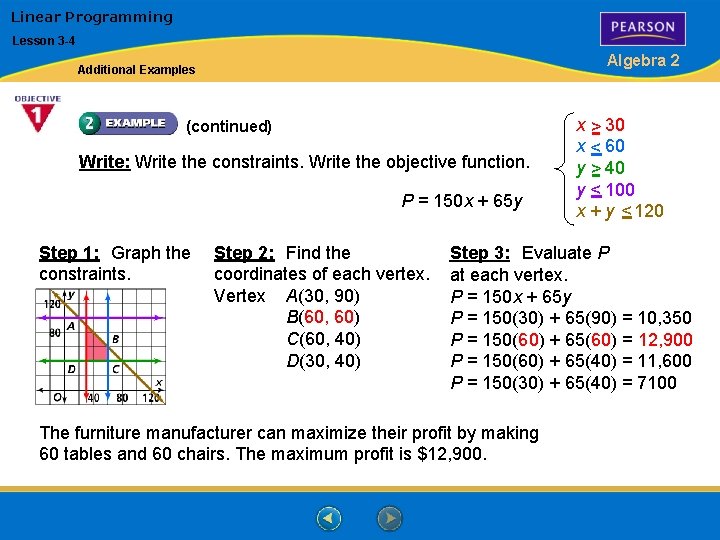
Linear Programming Lesson 3 -4 Algebra 2 Additional Examples (continued) Write: Write the constraints. Write the objective function. P = 150 x + 65 y Step 1: Graph the constraints. Step 2: Find the coordinates of each vertex. Vertex A(30, 90) B(60, 60) C(60, 40) D(30, 40) x > 30 x < 60 y > 40 y < 100 x + y < 120 Step 3: Evaluate P at each vertex. P = 150 x + 65 y P = 150(30) + 65(90) = 10, 350 P = 150(60) + 65(60) = 12, 900 P = 150(60) + 65(40) = 11, 600 P = 150(30) + 65(40) = 7100 The furniture manufacturer can maximize their profit by making 60 tables and 60 chairs. The maximum profit is $12, 900.

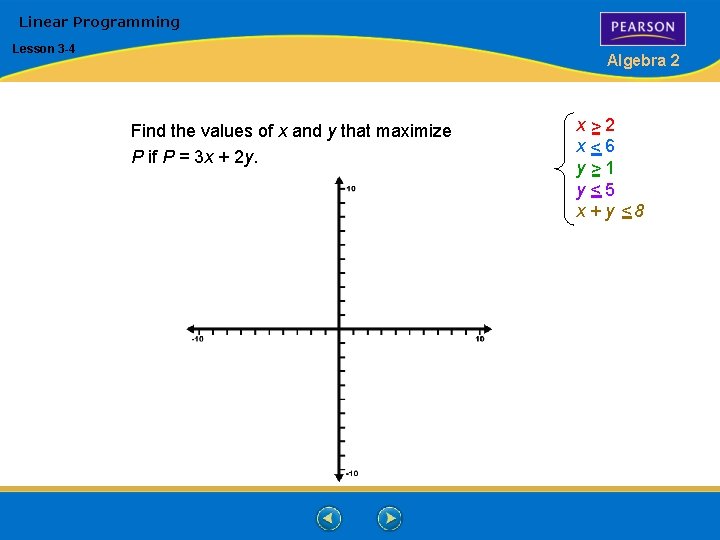
Linear Programming Lesson 3 -4 Algebra 2 Find the values of x and y that maximize P if P = 3 x + 2 y. x >2 x <6 y >1 y <5 x + y <8

Linear Programming Algebra 2 Homework pg 142 1, 5, 7, 10