Linear Programming Wyndor Glass Co 3 plants 2

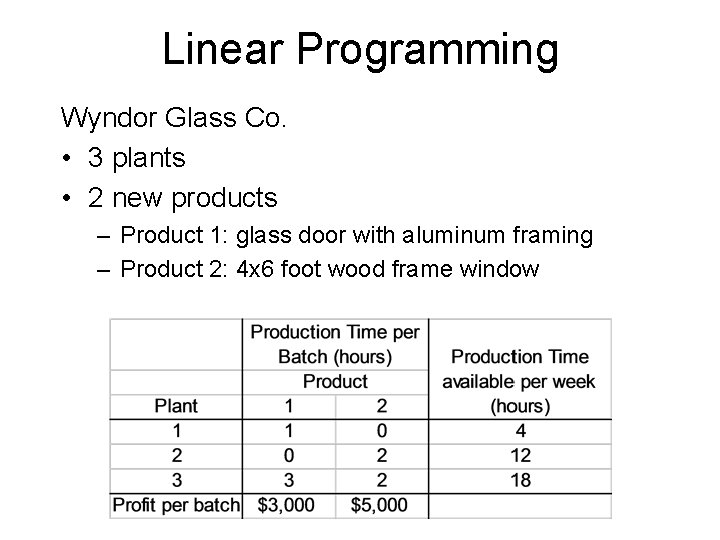
Linear Programming Wyndor Glass Co. • 3 plants • 2 new products – Product 1: glass door with aluminum framing – Product 2: 4 x 6 foot wood frame window

Wyndor Glass Problem cont. Objective: Determine what the production rates should be for the two products in order to maximize their total profit, subject to the restrictions imposed by the limited production capacities at each plant.

Wyndor Glass Problem cont. Optimal Solution: Product 1 – 2 batches/week Product 2 – 6 batches/week Profit - $36, 000

Intro. To Linear Programming Definition: Programming Problems Concerned with the use or allocation of scarce resources (labor, materials, machines, and capital), in the “best” possible manner so that costs are minimized or profit is maximized.

Intro. To Linear Programming Definition: Linear Programming Problems – The decision variables are non-negative – The objective function is linear – The constraint set is a set of linear equations Other programming problems: - Integer Non-linear (quadratic) Goal Paramteric

Why wide use of Linear Programming? • Wide variety of problems can be represented by an LP. • There exist efficient techniques for solving LPs. • Ease of analysis of data variation (sensitivity analysis)

Formulation of LP Model • Identify the decision variables. • Identify the problem constraints and express the constraints as a series of linear equations. • Identify the objective functions as a linear equation, and state whether the objective is maximization or minimization.

Formulation of Wyndor Glass Model • Identify the decision variables. x 1 – Number of batches of product 1 produced per week. x 2 – Number of batches of product 2 produced per week. • Identify the problem constraints and express the constraints as a series of linear equations. • Identify the objective functions as a linear equation, and state whether the objective is maximization or minimization.

Formulation of Wyndor Glass Model cont. •