LINEAR PROGRAMMING WORD PROBLEMS WITH ANSWERS 1 Mary

LINEAR PROGRAMMING WORD PROBLEMS WITH ANSWERS

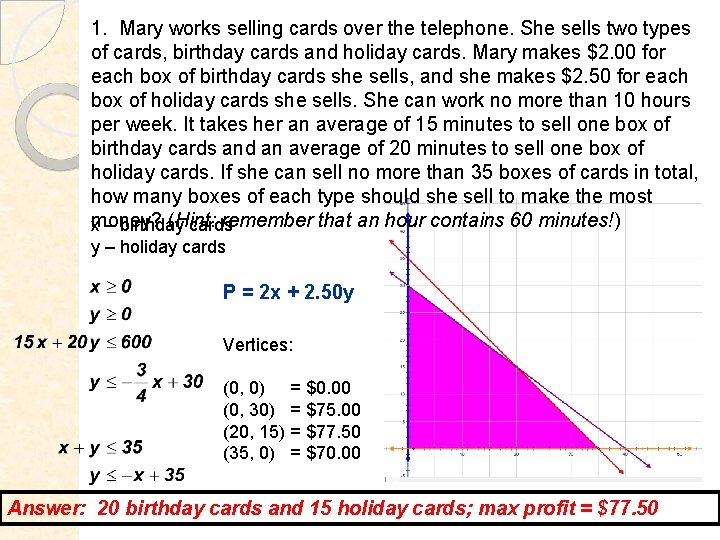
1. Mary works selling cards over the telephone. She sells two types of cards, birthday cards and holiday cards. Mary makes $2. 00 for each box of birthday cards she sells, and she makes $2. 50 for each box of holiday cards she sells. She can work no more than 10 hours per week. It takes her an average of 15 minutes to sell one box of birthday cards and an average of 20 minutes to sell one box of holiday cards. If she can sell no more than 35 boxes of cards in total, how many boxes of each type should she sell to make the most (Hint: remember that an hour contains 60 minutes!) xmoney? – birthday cards y – holiday cards P = 2 x + 2. 50 y Vertices: (0, 0) = $0. 00 (0, 30) = $75. 00 (20, 15) = $77. 50 (35, 0) = $70. 00 Answer: 20 birthday cards and 15 holiday cards; max profit = $77. 50

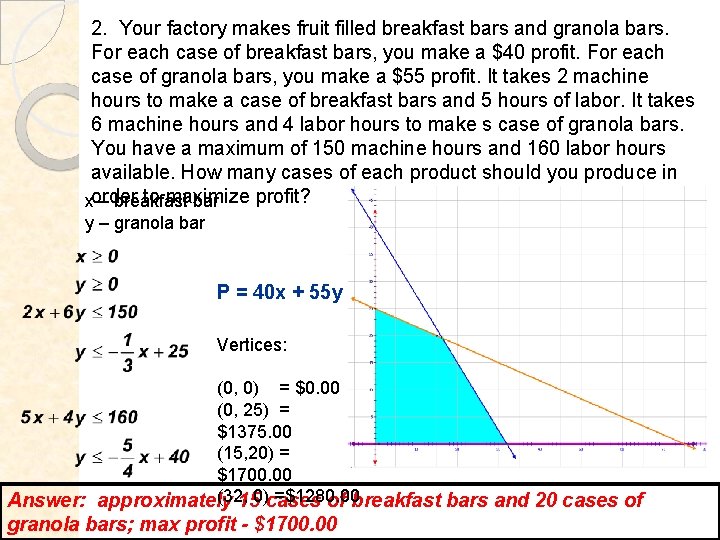
2. Your factory makes fruit filled breakfast bars and granola bars. For each case of breakfast bars, you make a $40 profit. For each case of granola bars, you make a $55 profit. It takes 2 machine hours to make a case of breakfast bars and 5 hours of labor. It takes 6 machine hours and 4 labor hours to make s case of granola bars. You have a maximum of 150 machine hours and 160 labor hours available. How many cases of each product should you produce in to maximize profit? xorder – breakfast bar y – granola bar P = 40 x + 55 y Vertices: (0, 0) = $0. 00 (0, 25) = $1375. 00 (15, 20) = $1700. 00 (32, =$1280. 00 Answer: approximately 150)cases of breakfast bars and 20 cases of granola bars; max profit - $1700. 00

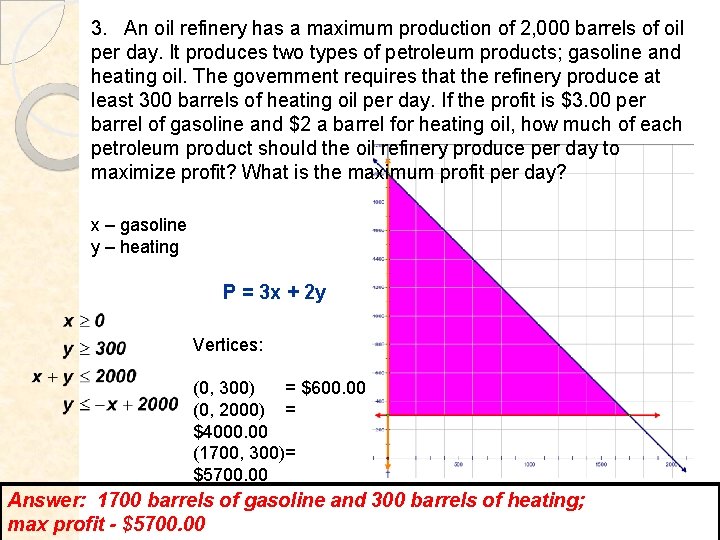
3. An oil refinery has a maximum production of 2, 000 barrels of oil per day. It produces two types of petroleum products; gasoline and heating oil. The government requires that the refinery produce at least 300 barrels of heating oil per day. If the profit is $3. 00 per barrel of gasoline and $2 a barrel for heating oil, how much of each petroleum product should the oil refinery produce per day to maximize profit? What is the maximum profit per day? x – gasoline y – heating P = 3 x + 2 y Vertices: (0, 300) = $600. 00 (0, 2000) = $4000. 00 (1700, 300)= $5700. 00 Answer: 1700 barrels of gasoline and 300 barrels of heating; max profit - $5700. 00

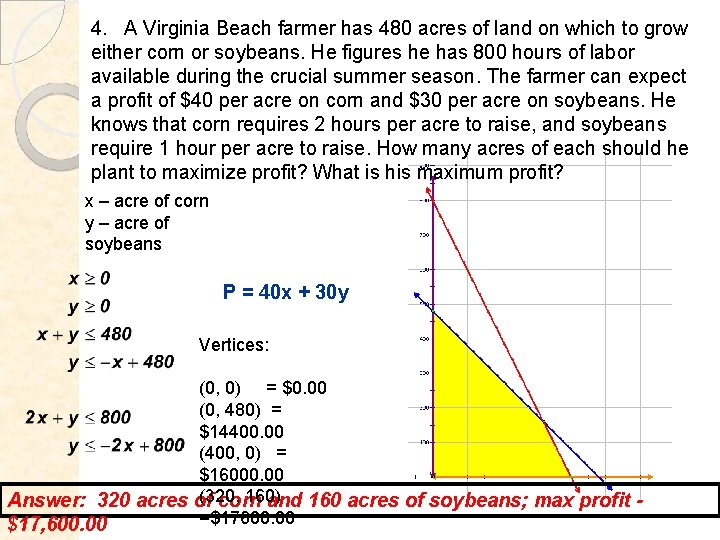
4. A Virginia Beach farmer has 480 acres of land on which to grow either corn or soybeans. He figures he has 800 hours of labor available during the crucial summer season. The farmer can expect a profit of $40 per acre on corn and $30 per acre on soybeans. He knows that corn requires 2 hours per acre to raise, and soybeans require 1 hour per acre to raise. How many acres of each should he plant to maximize profit? What is his maximum profit? x – acre of corn y – acre of soybeans P = 40 x + 30 y Vertices: (0, 0) = $0. 00 (0, 480) = $14400. 00 (400, 0) = $16000. 00 (320, 160) Answer: 320 acres of corn and 160 acres of soybeans; max profit =$17600. 00 $17, 600. 00

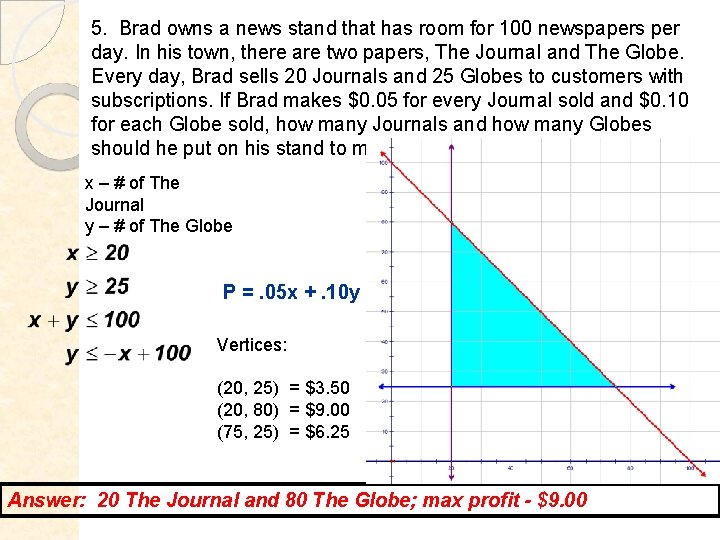
5. Brad owns a news stand that has room for 100 newspapers per day. In his town, there are two papers, The Journal and The Globe. Every day, Brad sells 20 Journals and 25 Globes to customers with subscriptions. If Brad makes $0. 05 for every Journal sold and $0. 10 for each Globe sold, how many Journals and how many Globes should he put on his stand to make the most money? x – # of The Journal y – # of The Globe P =. 05 x +. 10 y Vertices: (20, 25) = $3. 50 (20, 80) = $9. 00 (75, 25) = $6. 25 Answer: 20 The Journal and 80 The Globe; max profit - $9. 00

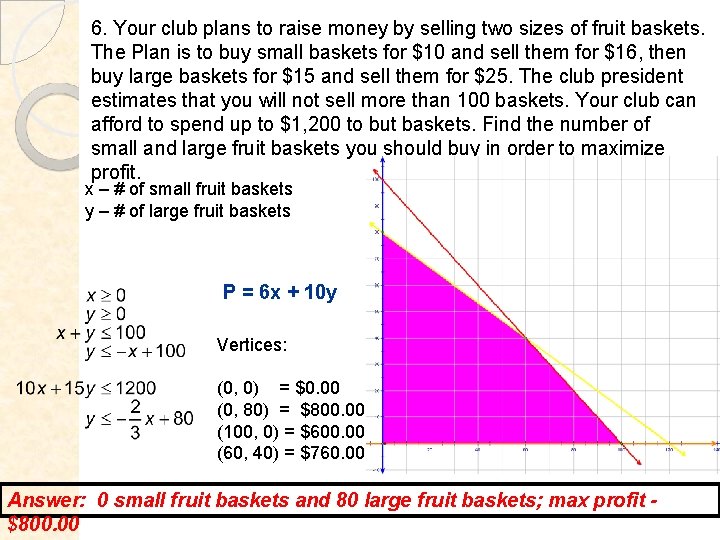
6. Your club plans to raise money by selling two sizes of fruit baskets. The Plan is to buy small baskets for $10 and sell them for $16, then buy large baskets for $15 and sell them for $25. The club president estimates that you will not sell more than 100 baskets. Your club can afford to spend up to $1, 200 to but baskets. Find the number of small and large fruit baskets you should buy in order to maximize profit. x – # of small fruit baskets y – # of large fruit baskets P = 6 x + 10 y Vertices: (0, 0) = $0. 00 (0, 80) = $800. 00 (100, 0) = $600. 00 (60, 40) = $760. 00 Answer: 0 small fruit baskets and 80 large fruit baskets; max profit $800. 00

LINEAR PROGRAMMING ACTIVITY SHEET WORD PROBLEMS WITH ANSWERS

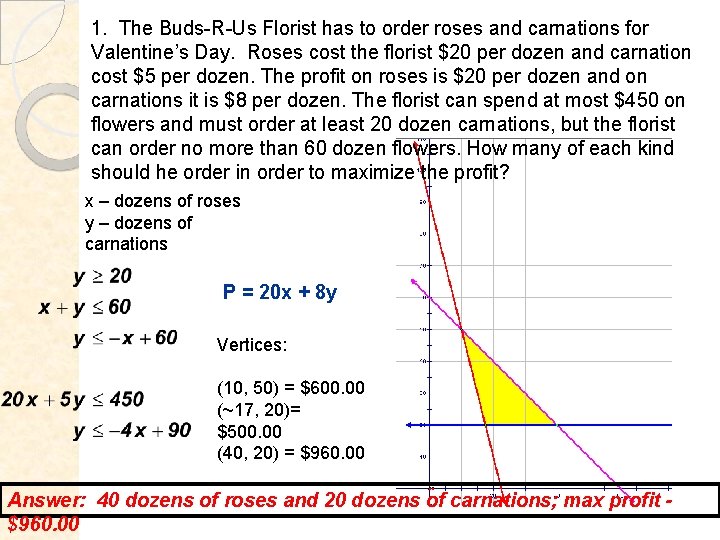
1. The Buds-R-Us Florist has to order roses and carnations for Valentine’s Day. Roses cost the florist $20 per dozen and carnation cost $5 per dozen. The profit on roses is $20 per dozen and on carnations it is $8 per dozen. The florist can spend at most $450 on flowers and must order at least 20 dozen carnations, but the florist can order no more than 60 dozen flowers. How many of each kind should he order in order to maximize the profit? x – dozens of roses y – dozens of carnations P = 20 x + 8 y Vertices: (10, 50) = $600. 00 (~17, 20)= $500. 00 (40, 20) = $960. 00 Answer: 40 dozens of roses and 20 dozens of carnations; max profit $960. 00

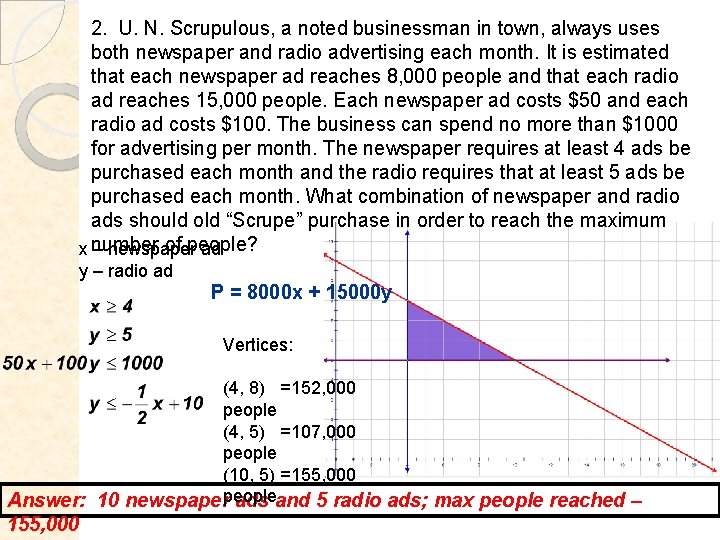
2. U. N. Scrupulous, a noted businessman in town, always uses both newspaper and radio advertising each month. It is estimated that each newspaper ad reaches 8, 000 people and that each radio ad reaches 15, 000 people. Each newspaper ad costs $50 and each radio ad costs $100. The business can spend no more than $1000 for advertising per month. The newspaper requires at least 4 ads be purchased each month and the radio requires that at least 5 ads be purchased each month. What combination of newspaper and radio ads should old “Scrupe” purchase in order to reach the maximum of people? x number – newspaper ad y – radio ad P = 8000 x + 15000 y Vertices: (4, 8) =152, 000 people (4, 5) =107, 000 people (10, 5) =155, 000 Answer: 10 newspaperpeople ads and 5 radio ads; max people reached – 155, 000

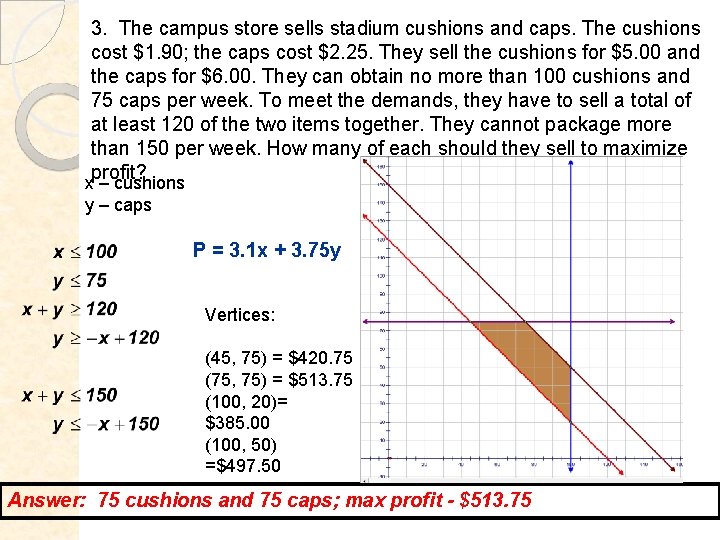
3. The campus store sells stadium cushions and caps. The cushions cost $1. 90; the caps cost $2. 25. They sell the cushions for $5. 00 and the caps for $6. 00. They can obtain no more than 100 cushions and 75 caps per week. To meet the demands, they have to sell a total of at least 120 of the two items together. They cannot package more than 150 per week. How many of each should they sell to maximize profit? x – cushions y – caps P = 3. 1 x + 3. 75 y Vertices: (45, 75) = $420. 75 (75, 75) = $513. 75 (100, 20)= $385. 00 (100, 50) =$497. 50 Answer: 75 cushions and 75 caps; max profit - $513. 75