Linear Programming Topics General optimization model LP model

Linear Programming Topics • General optimization model • LP model and assumptions • Manufacturing example • Characteristics of solutions • Sensitivity analysis • Excel add-ins

Deterministic OR Models Most of the deterministic OR models can be formulated as mathematical programs. "Program" in this context, has to do with a “plan” and not a computer program. Mathematical Program Maximize / Minimize Subject to z = f (x 1, x 2, …, xn) gi(x 1, x 2, …, xn) {} xj ≥ 0, j = 1, …, n = bi , i =1, …, m

Model Components • xj are called decision variables. These are things that you control • gi(x 1, x 2, …, xn) {} = bi are called structural (or functional or technological) constraints • xj ≥ 0 are nonnegativity constraints • f (x 1, x 2, …, xn) is the objective function

Feasibility and Optimality ( ) x 1 • A feasible solution x = . . . satisfies all the xn constraints (both structural and nonnegativity) • The objective function ranks the feasible solutions; call them x 1, x 2, . . . , xk. The optimal solution is the best among these. For a minimization objective, we have z* = min{ f (x 1), f (x 2), . . . , f (xk) }.

Linear Programming A linear program is a special case of a mathematical program where f(x) and g 1(x) , …, gm(x) are linear functions Linear Program: Maximize/Minimize z = c 1 x 1 + c 2 x 2 + • • • + cnxn Subject to ai 1 x 1 + ai 2 x 2 + • • • + ainxn xj uj, j = 1, …, n xj 0, j = 1, …, n {} = bi , i = 1, …, m

LP Model Components xj uj are called simple bound constraints x = decision vector = "activity levels" aij , cj , bi , uj are all known data goal is to find x = (x 1, x 2, …, xn)T (the symbol “ T ” means)

Linear Programming Assumptions (i) proportionality (ii) additivity (iii) divisibility (iv) certainty linearity

Explanation of LP Assumptions (i) activity j’s contribution to objective function is cjxj and usage in constraint i is aijxj both are proportional to the level of activity j (volume discounts, set-up charges, and nonlinear efficiencies are potential sources of violation) (ii) no “cross terms” such as x 112 x 5 may not appear in the objective or constraints.

Explanation of LP Assumptions (iii) Fractional values for decision variables are permitted (iv) Data elements aij , cj , bi , uj are known with certainty • Nonlinear or integer programming models should be used when some subset of assumptions (i), (ii) and (iii) are not satisfied. • Stochastic models should be used when a problem has significant uncertainties in the data that must be explicitly taken into account [a relaxation of assumption (iv)].

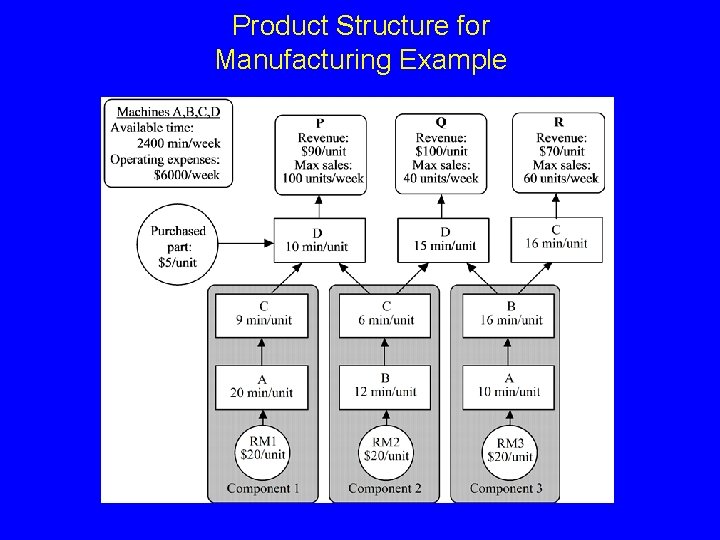
Product Structure for Manufacturing Example

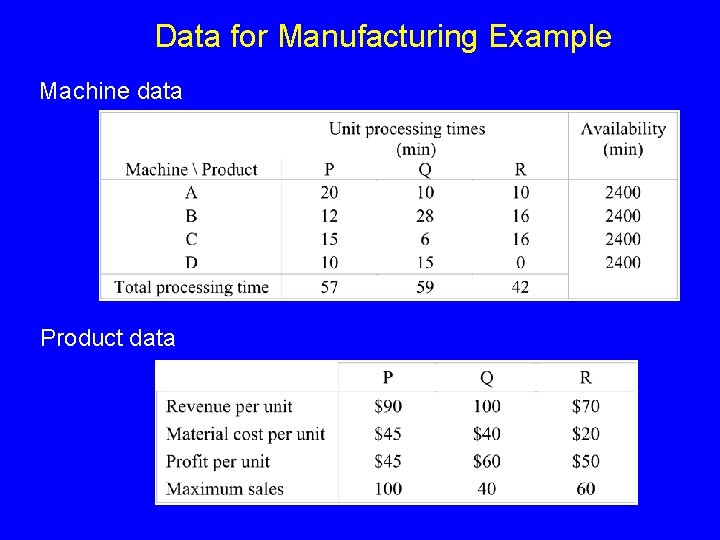
Data for Manufacturing Example Machine data Product data

Data Summary Selling price/unit Raw Material cost/unit Maximum sales Minutes/unit on A B C D P Q R 90 45 100 20 12 15 10 100 40 40 10 28 6 15 70 20 60 10 16 16 0 Machine Availability: 2400 min/wk Structural coefficients Operating Expenses = $6, 000/wk (fixed cost) Decision Variables x. P = # of units of product P to produce per week x. Q = # of units of product Q to produce per week x. R = # of units of product R to produce per week

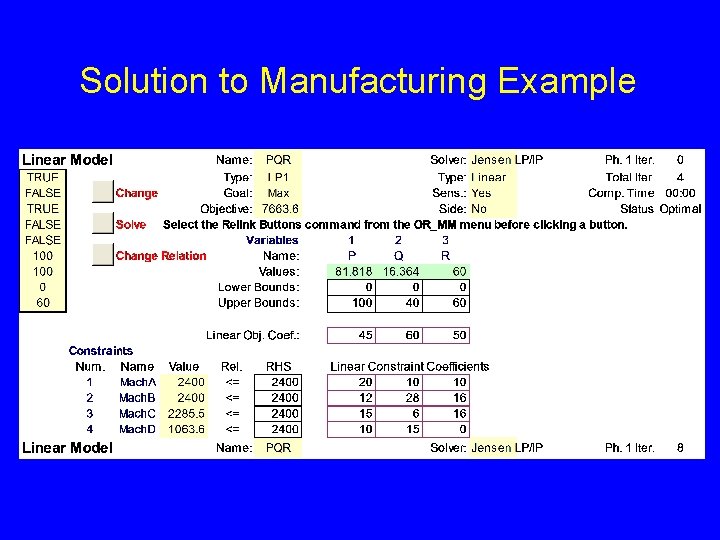
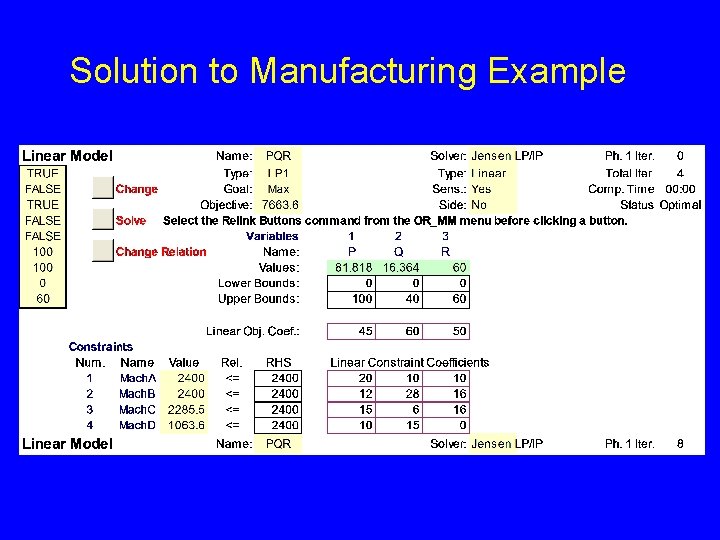
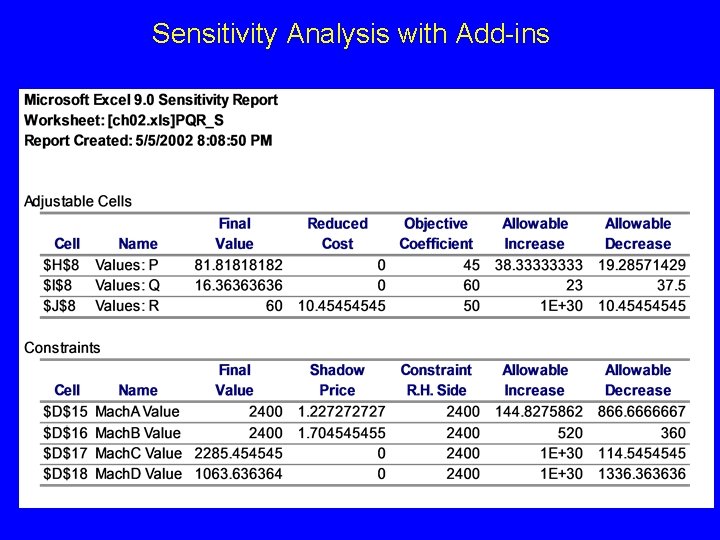
LP Formulation max z = 45 x. P s. t. 20 x. P 12 x. P 15 x. P 10 x. P + 60 x. Q + 50 x. R – 6000 + 10 x. Q + 10 x. R 2400 + 28 x. Q + 16 x. R 2400 + 6 x. Q + 16 x. R 2400 + 15 x. Q + 0 x. R 2400 x. P 100, x. Q 40, x. R 60 Are we done? x. P 0, x. Q 0, x. R 0 Objective Function Structural constraints demand nonnegativity Are the LP assumptions valid for this problem? Optimal solution x P* = 81. 82, * = 16. 36, x. Q x *R = 60

Discussion of Results for Manufacturing Example • Optimal objective value is $7, 664 but when we subtract the weekly operating expenses of $6, 000 we obtain a weekly profit of $1, 664. • Machines A & B are being used at maximum level and are bottlenecks. • There is slack production capacity in Machines C & D. How would we solve model using Excel Add-ins ?

Solution to Manufacturing Example

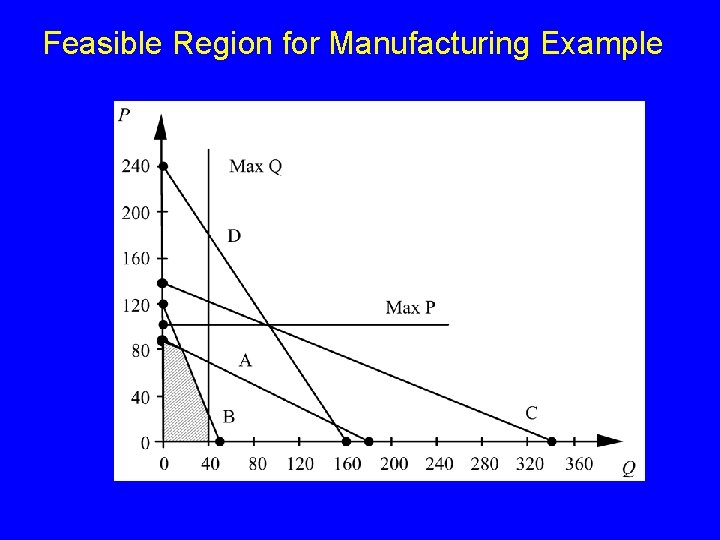
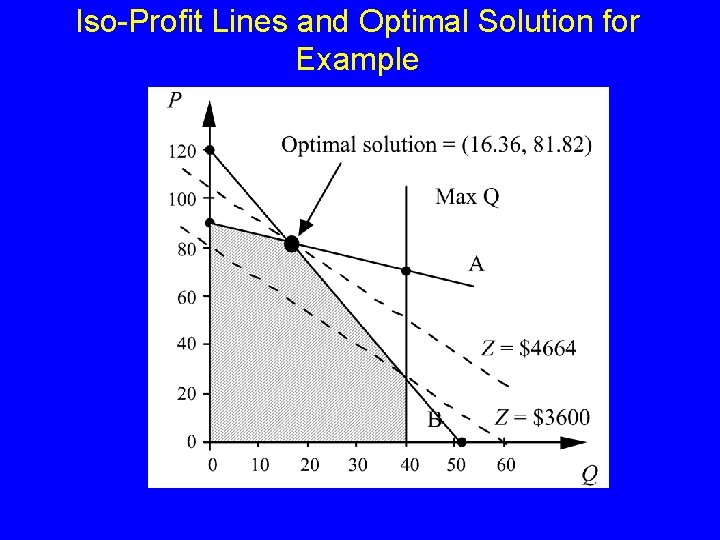
Characteristics of Solutions to LPs A Graphical Solution Procedure (LPs with 2 decision variables can be solved/viewed this way. ) 1. Plot each constraint as an equation and then decide which side of the line is feasible (if it’s an inequality). 2. Find the feasible region. 3. Plot two iso-profit (or iso-cost) lines. 4. Imagine sliding the iso-profit line in the improving direction. The “last point touched” as the iso-profit line leaves the feasible region is optimal.

Two-Dimensional Machine Scheduling Problem -- let x. R = 60 max z = 45 x. P s. t. 20 x. P 12 x. P 15 x. P 10 x. P + 60 x. Q + 3000 + + 10 x. Q 28 x. Q 6 x. Q 15 x. Q 1800 1440 2040 2400 Objective Function Structural constraints x. P 100, x. Q 40 demand x. P 0, x. Q 0 nonnegativity

Feasible Region for Manufacturing Example

Iso-Profit Lines and Optimal Solution for Example

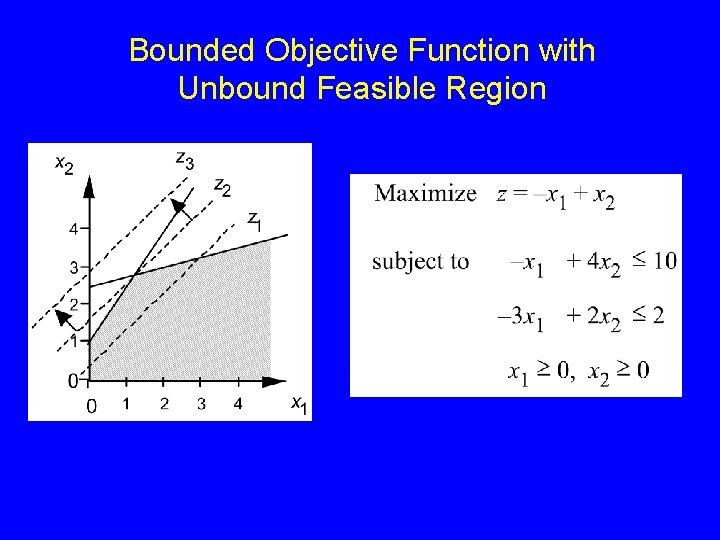
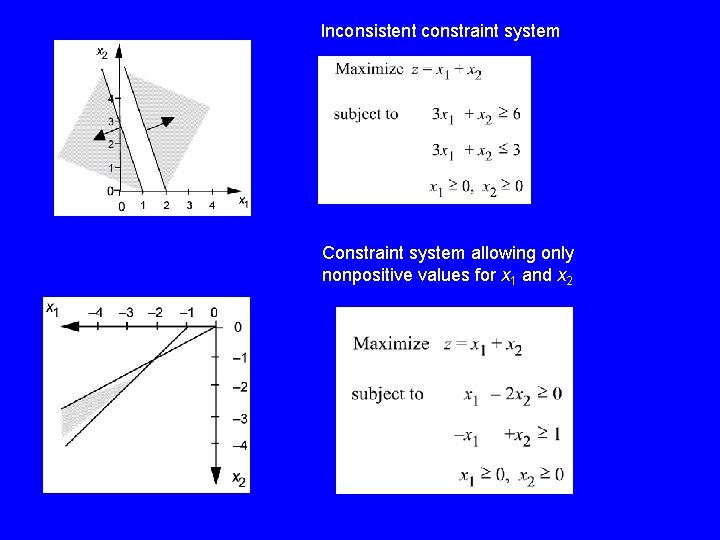
Possible Outcomes of an LP 1. Unique Optimal Solution 2. Multiple optimal solutions : Max 3 x 1 + 3 x 2 s. t. x 1+ x 2 1 x 1, x 2 0 3. Infeasible : feasible region is empty; e. g. , if the constraints include x 1+ x 2 6 and x 1+ x 2 7 4. Unbounded : Max 15 x 1+ 7 x 2 s. t. x 1 + x 2 1 x 1, x 2 0 (no finite optimal solution) Note: multiple optimal solutions occur in many practical (real-world) LPs.

Example with Multiple Optimal Solutions

Bounded Objective Function with Unbound Feasible Region

Inconsistent constraint system Constraint system allowing only nonpositive values for x 1 and x 2

Sensitivity Analysis Shadow Price on Constraint i Amount object function changes with unit increase in RHS, all other coefficients held constant Objective Function Coefficient Ranging Allowable increase & decrease for which current optimal solution is valid RHS Ranging Allowable increase & decrease for which shadow prices remain valid

Solution to Manufacturing Example

Sensitivity Analysis with Add-ins

What You Should Know About Linear Programming • • What the components of a problem are. How to formulate a problem. What the assumptions are underlying an LP. How to find a solution to a 2 -dimensional problem graphically. • Possible solutions. • How to solve an LP with the Excel add-in.