Linear Programming Problems 1 Definitions and terms in

Linear Programming Problems 1 Definitions and terms in LPP 2 Formulae of LPP 3 Solution by graphical method

Introduction Ø Linear programming (LP or linear optimisation) is a mathematical method for determining a way to achieve the best outcome (such as maximum profit or lowest cost) in a given mathematical model for some list of requirements represented as linear relationships. Ø Linear programming is a specific case of mathematical programming (mathematical optimisation). More formally, linear programming is a technique for the optimisation of a linear objective function, subject to linear equality and linear inequality constraints. Ø Its feasible region is a convex polyhedron, which is a set defined as the intersection of finitely many half spaces, each of which is defined by a linear inequality. Ø Its objective function is a real-valued affine function defined on this polyhedron.

5. 1. Definition and Terms of LPP 1) Linear Function : Definition : A function f(x 1, x 2, . . . xn) of x 1, x 2, . . . xn is a linear function if and only if for some set of constants c 1, c 2, . . . . cn f(x 1, x 2, . . . xn) = c 1 x 1 + c 2 x 2 +. . + cnxn Examples: i) x 1 ii) 5 x 1+ 6 x 4 - 2 x 2+1 iii) 3

5. 1. Definition and Terms of LPP 2)Linear Inequalities : Definition : For any linear functions f(x 1, x 2, . . . xn) and any number b, the inequalities. f(x 1, x 2, . . . xn) £ b and f(x 1, x 2, . . . xn) > b are linear inequalities. Examples : i) x 1 + x 2£ 4 ii) 5 x 1 - 4 > 0 Note : If an inequality can be rewritten as a linear inequality then it is one. Thus x 1 + x 2£ 3 x 3 is a linear inequality because it can be rewritten as x 1+x 2 -3 x 3£ 0. Even x 1 / x 2 £ 4 is a linear inequality because it can be rewritten as x 1 - 4 x 2£ 0. Note that x 1 / x 2 + x 3£ 4 is not a linear inequality, however.

5. 1. Definition and Terms of LPP 3) Linear Equalities : Definition : For any linear function f(x 1, x 2, . . . xn) and any number b, the equality f(x 1, x 2, . . . xn) = b is a linear equality. 4)LP (Linear Programming) : Definition: A linear Programming problem (LP) is an optimisation problem for which : a)We attempt to maximize (or minimize) a linear function of the decision variables. (objective function) b)The values of the decision variables must satisfy a set of constraints, each of which must be a linear inequality or linear equality. c)A sign restriction on each variable. For each variable xi the sign restriction can either say i) xi> 0, ii) xi£ 0, iii) xi unrestricted (urs).

5. 1. Definition and Terms of LPP 5) Solution : A Solution to a linear program is a setting of the variables. 6)Feasible region: The feasible region in a linear program is the set of all possible feasible solutions. 7)Feasible solution: A feasible solution to a linear program is a solution that satisfies all constraints. 8)Basic and Non basic variables and solutions : Consider a linear programming problem in which all the constraints are equalities (conversion can be accomplished with slack and excess variables. ) Definitions : 1)If there are n variables and m constraints, a solution with at most m non-zero values is a basic solution. 2)In a basic solution, n-m of the zero-valued variables are considered non-basic variables and the remaining m variables are considered basic variables.

5. 1. Definition and Terms of LPP 9) Dual of LPP : a)Meaning : Duality is the state of having two distinct but related parts. The concept represents the possibility of an intriguing universal state that has been proposed and debated in diverse disciplines. For example, philosophers speak of mind and matter as underlying all known phenomena; theologians propose the underlying principles of good and bad, and the doctrine that people have both a physical and a spiritual nature; and chemists have proved that every definite compound consists of two parts having opposite electrical activity. It turns out that every LP problem has a related problem called the dual problem or dual. The dual is formulated from information contained in the original problem called the primal problem or primal and when solved, the dual provides all essential information about the solution to the primal.

5. 1. Definition and Terms of LPP b) Dual Problem Formulation: The parameters of an original (primal) LP problem provide all of the information needed to formulate the corresponding dual problem. The following example illustrates the formulation of the dual for a simple primal. Let us make some observations about the primal and dual problems in the above example. 1) The primal is maximization problem, and the dual is minimization problem. The sense of optimisation is always opposite for corresponding primal and dual problems. 2) The primal has three variables and two constraints; the dual has two variables and three constraints. The number of variables in the primal (n) always equals the number of constraints in the dual and vice versa. 3) The coefficients in constraint 1 of the primal are the column coefficients for the first dual variable (y 1) in the three dual constraints. The same relationship is true for constraint 2 of the primal and the column for y 2 in the dual. The technological coefficients (aij) in the primal are transposed to ajiin the dual; that is, row coefficients in primal constraints become column coefficients in dual constraints and vice versa, or the matrix A in the primal becomes the transposed matrix AT in the dual.

5. 1. Definition and Terms of LPP 4) The objective function coefficients for variables x 1, x 2, and x 3 in the primal become the RHS constants for constraints 1 -3 of the dual. The objective function coefficient for the jth primal variable (cj) equals the RHS constant for the ith dual constraint. 5) The RHS constants in constraints 1 and 2 of the primal equal the objective function coefficients for y 1 and y 2 in the dual. The RHS constant for the ith primal constraint (bi) equals the objective function coefficient for the ith dual variable. The above example illustrates the formulation of the dual problem from as so called canonical primal problem, that is, a maximization problem having all constraints and all variables non negative. Given a canonical primal, the resulting dual is a canonical dual problem, that is a minimization problem with all constraints and all variables non-negative. The symmetry between a canonical primal and its canonical dual is illustrated by the following generalisations.

5. 1. Definition and Terms of LPP c) Symmetry between Canonical Primal Problem and Canonical Dual Problem : Canonical Primal Canonical Dual Maximize Minimize Subject to i = 1, . . . , m j = 1, . . . , n Thus the transformation from primal to dual is perfectly symmetric: In the objective function, max becomes min, cj becomes bi, and xj becomes y; in the constraints, aij becomes aji, xj becomes yi, bi becomes cj, and becomes. Interesting phenomenon, isn't it ? d) Dual Transformation Rules : Obviously, original problems are not usually canonical primal. In such cases the rules formulating the dual are more comprehensive the following table presents primal / dual transformation rules formulating the dual of any primal. Note that in this case the primal is the right column, and the dual is the left column in table of rules. In effect, we ''mapped'' from right to left in transforming a min primal to a max dual.

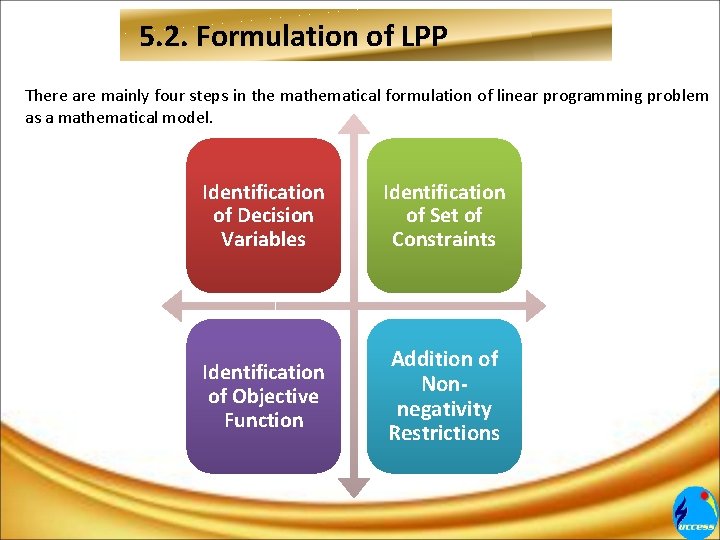
5. 2. Formulation of LPP There are mainly four steps in the mathematical formulation of linear programming problem as a mathematical model. Identification of Decision Variables Identification of Set of Constraints Identification of Objective Function Addition of Nonnegativity Restrictions

5. 2. Formulation of LPP a)Identification of Decision Variables : Identify the decision variables and assign symbols x and y to them. These decision variables are those quantities whose values we wish to determine. b)Identification of Set of Constraints : Identify the set of constraints and express them as linear equations/ inequations in terms of the decision variables. These constraints are the given conditions. c)Identification of Objective Function : Identify the objective function and express it as a linear function of decision variables. It might take the form of maximizing profit or production or minimizing cost. d)Addition of Non-negativity Restrictions : Add the non-negativity restrictions on the decision variables, as in the physical problems, negative values of decision variables have no valid interpretation.

5. 3. Solution by Graphical Method Linear programming with two decision variables can be solved graphically, Although the method is quite simple the principle of solution is based on certain analytical concepts. This is one of the simplest method to solve Linear Programming Problems : Steps: 1)Treat each inequality into equality. 2)Plot the point and Draw line on Graph for equality. 3)Draw the region whether it is towards the origin i. e. (0, 0) or away from origin shown by ( ) arrow. 4)Find out common feasible region. This may be open region or closed polygon. 5)The optimum value is always at vertices of polygon. 6)Substitute the values of vertices in minimize or maximize objective and find the optimum solution. That is for maximize objective where the solution is maximum and for minimize objective where the solution is minimum

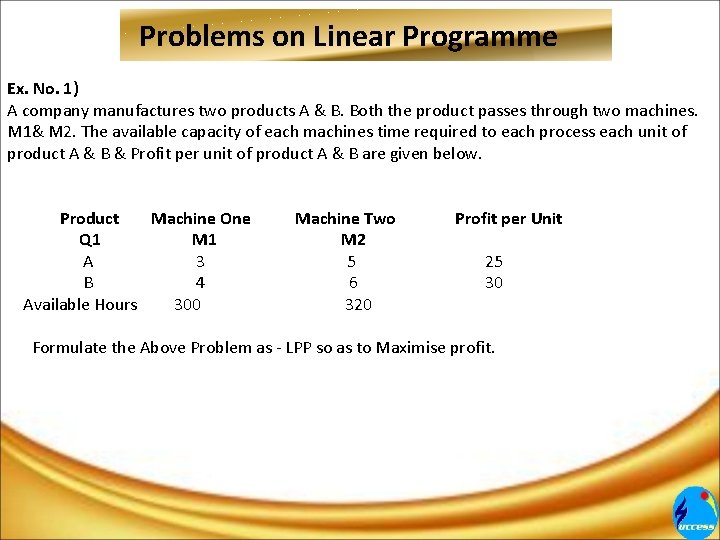
Problems on Linear Programme Ex. No. 1) A company manufactures two products A & B. Both the product passes through two machines. M 1& M 2. The available capacity of each machines time required to each process each unit of product A & B & Profit per unit of product A & B are given below. Product Machine One Q 1 M 1 A 3 B 4 Available Hours 300 Machine Two M 2 5 6 320 Profit per Unit 25 30 Formulate the Above Problem as - LPP so as to Maximise profit.

5. 4. Problems on Linear Programme Solution : I)Decision Variable : The profit is depend upon the No. of products A & B to be produced. Let the No. of products A be produced = X & Let the No. of product B be produce = y. II)Objective Function : Our objectives is to maximize profit. To Maximize profit = f = 25 x + 30 y. . . (I) III)Constraints : M 1 = M 1 requires 3 hours for product A and 4 hours for product B but available Hours are 300. 3 x + 4 y must be 300. . . (II) M 2 = M 2 requires 5 hours for product A and 6 hours for product B but available hours are 320. 5 x + 6 y 320. . . (III) IV)Formulation of L. P. P : To maximize profit = f = 25 x + 30 y Subject to = 3 x + 4 y 300 5 x + 6 y 320 x> 0 y> 0

5. 4. Problems on Linear Programme Ex. No. 2) A manufacturer make two types of Lamps A & B requiring treatment by a cutter a finisher. Lamp A requires 2 hours of cultures time & 1 hour of finisher's time. Lamp B requires 1 hour of cutter & 2 hours of finishers time. The cutter has 104 hours & Finisher has 76 hours of available time; each month profit on 1 Lakh. A is Rs 6 & on Lamp B is Rs. 11. Formulate the given problem as L. L. P. Production Culture Finisher Profit per hr. A 2 1 6 B 1 2 11 Available Hours 104 76

5. 4. Problems on Linear Programme

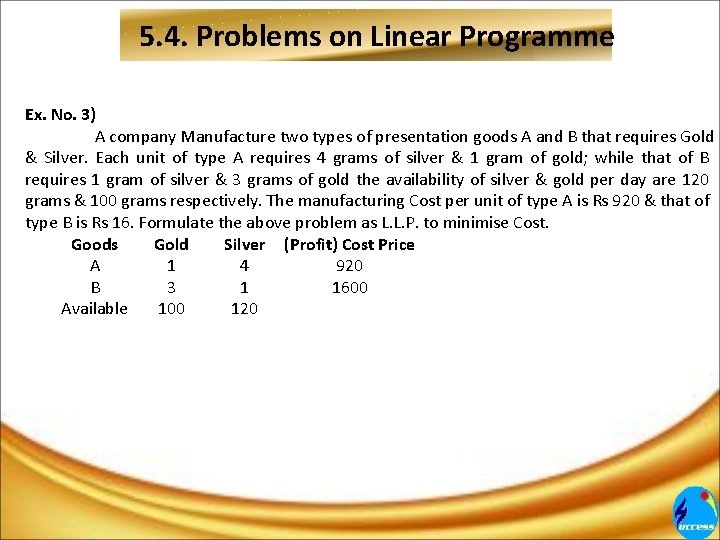
5. 4. Problems on Linear Programme Ex. No. 3) A company Manufacture two types of presentation goods A and B that requires Gold & Silver. Each unit of type A requires 4 grams of silver & 1 gram of gold; while that of B requires 1 gram of silver & 3 grams of gold the availability of silver & gold per day are 120 grams & 100 grams respectively. The manufacturing Cost per unit of type A is Rs 920 & that of type B is Rs 16. Formulate the above problem as L. L. P. to minimise Cost. Goods Gold Silver (Profit) Cost Price A 1 4 920 B 3 1 1600 Available 100 120

5. 4. Problems on Linear Programme Solution:

5. 4. Problems on Linear Programme

5. 4. Problems on Linear Programme Ex. No. 4) A dealer wishes to purchase a No. of fans &Sewning Machine he had only Rs 5760 to invest & he has space for almost 20 items a fan cost Rs. 360 & a sewn machine Rs. 240 his expectation is that he can sale a fan at a profit of Rs. 22 and sewning machine at a profit of Rs. 18 assuming that he can raise all the items can by formulate his problem L. L. P to maximize his profit. Fans 350 Sewing 240 Available 5760

5. 4. Problems on Linear Programme

5. 4. Problems on Linear Programme

5. 4. Problems on Linear Programme Ex. No. 5) A company Manufactures two types of toys A and B. Each Toy of type A requires 1 minutes for costing and 1 minutes of for assembling. Each toy of type B requires 3 min for cutting and 4 min for assembling. Their are 150 min available for cutting and 160 min for assembling on selling a toy of type A company gets a profit of Rs. 10 and that on selling a toy of type B company gets a profit of Rs. 20 formulates the problem as L. P. P. to maximize the profit. Toys Cutting Assembling Profit A 2 1 10 B 3 4 20 Available Time 180 160

5. 4. Problems on Linear Programme

5. 4. Problems on Linear Programme