Linear Programming Presented By Kuldeep Kumar So C

Linear Programming Presented By: Kuldeep Kumar, So. C, NUS

Contents � Introduction Ø A Linear Programming Problem Ø Formulating a LP Problem Ø Some LP Terminologies Ø Standard and Slack form � Solution to LP problems Ø Solution to a LP problem ( a geometric overview) Ø Simplex Method Ø Pivoting Ø Formal Simplex algorithm Ø Finding Initial solution Ø Duality � Conclusion 2 Linear Programming 21 -10 -2021

Text Book ØCormen H. T. , Leiserson C. E. , Rivest R. L. and Stein C. , “ Introduction to Algorithms”, Chapter 29, Second Ed. , PHI, India, 2006. References: 1. 2. 3. David G. Luenberger, Linear and Nonlinear Programming, Chapter 2 -4, 2 nd edition, Kluwer Academic Publishers, USA. Thomas S. Ferguson, Linear Programming- A concise Introduction, http: //www. math. ucla. edu/~tom/LP. pdf, website accessed on February 12, 2012 Karen Daniels, Linear Programming, Lecture notes on Analysis of Algorithm, http: //www. cs. uml. edu/~kdaniels/courses/ALG_503_S 12. html, website accessed on March 05, 2012. . 3 Linear Programming 21 -10 -2021

Introduction ØA Linear Programming Problem ØFormulating a LP Problem ØSome LP Terminologies ØStandard and Slack form. 4 Linear Programming 21 -10 -2021

A Linear Programming Problem �Linear programming: �Technique of optimizing a linear objective function expressed in terms of certain variables subject to some linear constraints imposed on these variables. Given a set of real numbers c 1, c 2, …, cn and a set of variables x 1, x 2, …, xn , A linear function f can be formulated as optimizing : subject to set of linear constraints such as: 5 Linear Programming 21 -10 -2021

Formulating a LP Problem �Consider a political problem: Total No. of voters in each region 100, 000 voters Policy 200, 000 voters 50, 000 voters Urban Suburban Rural Build Road -2 5 3 Gun Control 8 2 -5 Agriculture 0 0 10 LPG subsidy 10 0 -2 Thousands of voters who could be won with $1, 000 of advertisement By hit and trial method, one possible strategy to win the election is: • Spent $20, 000 of advertising to building roads, $0 to gun control, $4, 000 to agriculture and $9, 000 to a LPG subsidy. • But, Is the strategy gives us an optimum advertizing investment? 6 Linear Programming 21 -10 -2021

Formulating a LP Problem cont… Ø Our Objective is to “Win election by winning at least half the registered votes in each region while minimizing the advertizing cost”. Ø Representing the problem as a Linear Program: � Introduce 4 variables x 1, x 2 , x 3 , x 4 denoting the number of thousands of dollars spent on advertising on building roads, gun control, agriculture and LPG subsidy respectively. � The problem can be formulated as: urban suburban rural 7 Linear Programming Thousands of voters representing majority. 21 -10 -2021

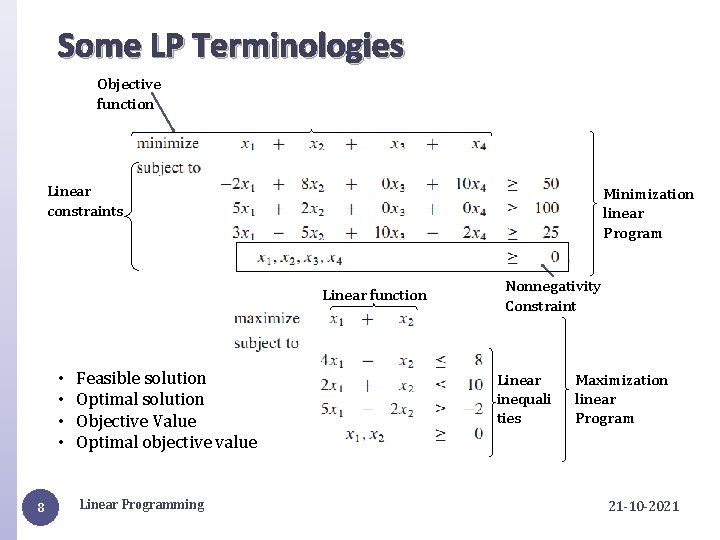
Some LP Terminologies Objective function Linear constraints Minimization linear Program Linear function • • 8 Feasible solution Optimal solution Objective Value Optimal objective value Linear Programming Nonnegativity Constraint Linear inequali ties Maximization linear Program 21 -10 -2021

Standard and Slack form �Canonical forms useful for specifying and working with linear programs. �Standard form: �Informally, in standard form, a linear program is the maximization of a linear function subject to linear inequalities. �Slack form: �In slack form, a linear program is the maximization of a linear function subject to linear equalities. 9 Linear Programming 21 -10 -2021

Standard and Slack form cont… Converting linear program in Standard form: �A linear program in standard form is represented as: Where aij , bi , cj ; for i=1, 2, …m and j=1, 2, …, n are the set of real numbers. 10 Linear Programming 21 -10 -2021

Standard and Slack form cont… Converting a LP in Standard form: cont… � A linear program may not be in standard form because of any these four possible reasons: 1. The objective function may be a minimization rather than a maximization. 2. There may be variables without non-negativity constraints. 3. There may be equality constraints having an equal sign instead of a less-than-or-equal-to sign. 4. There may be inequality constraints, but instead of having a less-than-or-equal-to sign, they have a greater-than-or-equal-to sign. 11 Linear Programming Negate coefficients (1) 21 -10 -2021

Standard and Slack form cont… Converting a LP in Standard form: cont… 2. If xi has no non-negativity constraints: • Replace each occurrence of xi with xi'-xi''. • Add constraints: xi' 0 and xi'' 0. Removing nonnegative Constraints(2) Transforming equality constraints to inequality constraints (3) Transforming into less than or equal to constraints (4) 12 Linear Programming 21 -10 -2021

Standard and Slack form cont… Converting linear program in Slack form: Recall: In slack form, a linear program is the maximization of a linear function subject to linear equalities. � Transform all constraints except non-negativity ones into equalities. x n+i are called slack variables as they measure the difference between left and right hand side of the equations. 13 Linear Programming 21 -10 -2021

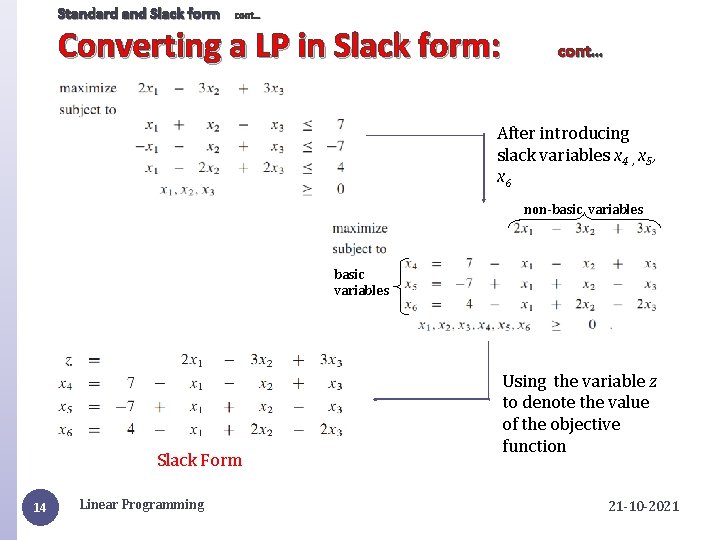
Standard and Slack form cont… Converting a LP in Slack form: cont… After introducing slack variables x 4 , x 5, x 6 non-basic variables Slack Form 14 Linear Programming Using the variable z to denote the value of the objective function 21 -10 -2021

Solution to LP problems ØSolution to a LP problem ( a geometric overview) ØSimplex Method Ø Pivoting Ø Formal Simplex algorithm Ø Finding Initial solution Ø Duality . 15 Linear Programming 21 -10 -2021

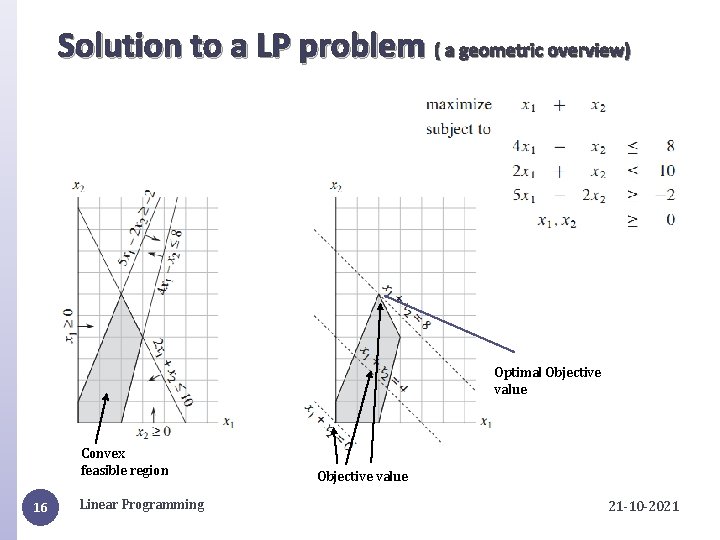
Solution to a LP problem ( a geometric overview) Optimal Objective value Convex feasible region 16 Linear Programming Objective value 21 -10 -2021

Simplex Method �Based on Geometric View: �Starts from some vertex of the simplex and performs a sequence of iterations. �In each iteration, moves along an edge of the simplex from a current vertex to a neighboring vertex having objective value is no smaller than that of the current vertex. �The simplex algorithm terminates when it reaches a local maximum. �Since, feasible region is convex and the objective function is linear, this local optimum is actually a global optimum. 17 Linear Programming 21 -10 -2021

Simplex Method (Algebraic View) �Basic Steps: 1. Write the given linear program into the slack form. 2. Find the initial basic solution by setting all non-basic variables to 0 and compute all basic variables. 3. Iterate from one slack form to another by making a basic variable as nonbasic and a nonbasic variable as basic in such a way that � Objective value of the function does not decreases. Select a nonbasic variable xe having positive coefficient in objective function 2. Increase value of xe as much as possible without violating any of constraints, and identify tightest constraint. Find basic variable x l corresponding to the tightest constraint. 3. Swap the role of xl and xe 1. � Underlying LP problem does not change � The feasible solutions keep the same. 18 Linear Programming 21 -10 -2021

Example Consider a Linear program given in standard form Maximize Subject to: 3 x 1+x 2+2 x 3 x 1+x 2+3 x 3 30 2 x 1+2 x 2+5 x 3 24 4 x 1+x 2+2 x 3 36 x 1, x 2, x 3 0 Ø Step 1: Change to slack form: z= 3 x 1+x 2+2 x 3 x 4=30 - x 1 -x 2 -3 x 3 x 5=24 - 2 x 1 -2 x 2 -5 x 3 x 6=36 - 4 x 1 -x 2 -2 x 3 x 1, x 2, x 3, x 4, x 5, x 6 0 Ø Step 2: Initial Basic solution: Recall: To get basic sol. , set each non-basic variable to 0. (x 1, x 2, x 3, x 4, x 5, x 6) =(0, 0, 0, 30, 24, 36). �The result is z=3 0+0+2 0=0. Not maximum. 19 Linear Programming 21 -10 -2021

Example cont… Ø Step 3: Iteration (Recall) Select a nonbasic variable xe having positive coefficient in objective function 2. Increase value of xe as much as possible without violating any of constraints, and identify tightest constraint. Find basic variable x l corresponding to the tightest constraint. 3. Swap the role of xl and xe. 1. In objective function x 1+x 2+2 x 3, each variable x 1, x 2, x 3 has positive value. Let us try to increase the value of x 1. 2. 30: x 4 will be OK; 12: x 5; 9: x 6. So only to 9 corresponding to x 6. It act as xl 3. Change x 1 to basic variable and change the equations accordingly. 20 Linear Programming 21 -10 -2021

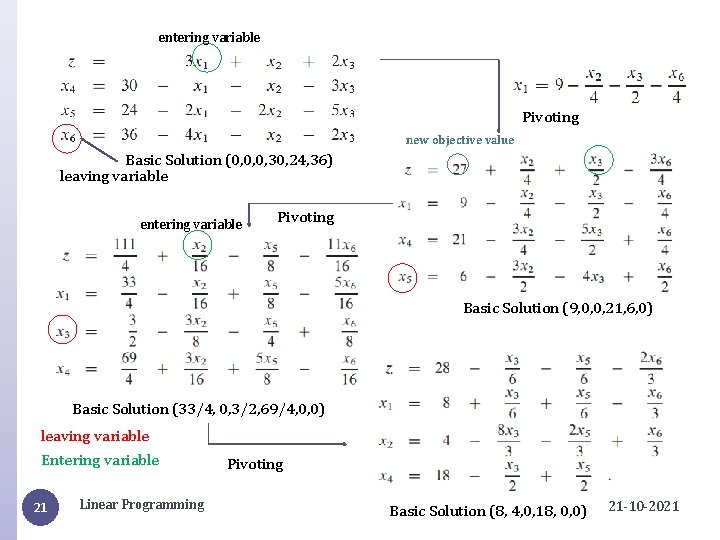
entering variable Pivoting new objective value Basic Solution (0, 0, 0, 30, 24, 36) leaving variable entering variable Pivoting Basic Solution (9, 0, 0, 21, 6, 0) Basic Solution (33/4, 0, 3/2, 69/4, 0, 0) leaving variable Entering variable 21 Linear Programming Pivoting Basic Solution (8, 4, 0, 18, 0, 0) 21 -10 -2021

Recall: Slack form �A slack form can also be represented as a tuple (N, B, A, b, c, v) denoting the slack form: Where : all variables x are non-negatives N, B denotes the set of non-basic and basic variables resp. and A is a matrix having elements aij. 22 Linear Programming 21 -10 -2021

Recall: Slack form (cont…) As an example, in the slack form given as: 23 Linear Programming 21 -10 -2021

Pivoting Rewrite the equation that has xl on LHS to have xe on LHS Update remaining equations by substituting RHS of new equation for each occurrence of xe. Do the same for objective function. Update sets of nonbasic, basic variables. 24 Linear Programming Abbreviations N: indices set of nonbasic variables B: indices set of basic variables A: aij b: bi c: ci v: constant coefficient. e: index of entering variable l: index of leaving variable z=v+ j Ncjxj xi=bi- j Naijxj for i B 21 -10 -2021

Formal Simplex algorithm The various issues to be considered during solving a linear programming problem are : �How do we determine whether a linear program is feasible? �What do we do if the linear program is feasible, but the initial basic solution is not feasible? �How do we determine whether a linear program is unbounded? �How do we choose the entering and leaving variables? 25 Linear Programming Procedure INITIALIZE-SIMPLEX (A, b, c) is called by SIMPLEX (A, b, c) to determine whether a problem is feasible. And if it is, INITIALIZE-SIMPLEX (A, b, c) returns a slack form in which the initial basic solution is feasible. These two issues are considered by SIMPLEX (A, b, c) procedure during its execution 21 -10 -2021

Formal Simplex Algorithm cont… initial basic feasible solution Return initial basic feasible solution. detects unbounded-ness Abbreviations N: indices set of nonbasic variables B: indices set of basic variables A: aij b: bi c: ci v: constant coefficient. e: index of entering variable l: index of leaving variable z=v+ j Ncjxj xi=bi- j Naijxj for i B optimal solution 26 Linear Programming 21 -10 -2021

Formal Simplex Algorithm cont… Finding Initial solution [INITIALIZE-SIMPLEX (A, b, c)] Recall: Procedure INITIALIZE-SIMPLEX determines that whether a linear program has any feasible solutions, and if it does, gives a slack form for which the basic solution is feasible. � But, it may be the case that a linear program can be feasible, yet the initial basic solution may not be feasible. Corresponding Slack form Example of an LP problem whose initial basic sol. is not feasible 27 Initial basic solution (0, 0, 2, -4) -violating the constraints By Inspection, even it is not clear whether this LP has any feasible solution Linear Programming 21 -10 -2021

Formal Simplex Algorithm cont… Finding Initial solution [INITIALIZE-SIMPLEX (A, b, c)] cont… � In order to determine whether a linear program (L) has any feasible solutions, formulate an auxiliary linear program (Laux) satisfying Lemma 1. � Lemma 1: Let L be a linear program in standard form, Let x 0 be a new variable, and let Laux be the following linear program with n-1 variables: Then L is feasible if and only if the optimal objective value of L aux is 0. 28 Linear Programming 21 -10 -2021

Formal Simplex Algorithm cont… Finding Initial solution [INITIALIZE-SIMPLEX (A, b, c)] cont… Lemma 1 cont. . � Suppose that L has a feasible solution given by: i. e. , we have � Then the solution combined with is a feasible solution to Laux with objective value 0. � Laux has the objective function to maximize -x 0, this solution must be optimal for Laux. � Conversely, �suppose that the optimal objective value of Laux is 0. Then and thus remaining solution values of satisfy the constraints of L. 29 Linear Programming 21 -10 -2021

Formal Simplex Algorithm cont… Finding Initial solution [INITIALIZE-SIMPLEX (A, b, c)] cont… �Recall the LP problem (given on top right). �We know that this problem has not initial feasible solution. �Let us find whether it Formulating Laux has any feasible solution. �To do so, formulate it as auxiliary linear program (given on bottom right) 30 Linear Programming 21 -10 -2021

Formal Simplex Algorithm cont… Finding Initial solution [INITIALIZE-SIMPLEX (A, b, c)] cont… � Recall: From Lemma 1, If the optimal objective value of L aux is 0, then the original linear program has a feasible solution otherwise solution is infeasible. � To find optimum objective value of Laux , convert it into slack form and solve the linear program. entering Pivoting leaving most negative (restrictive) leaving Corresponding slack form of Laux associated basic solution (0, 0, 0, 2, -4) which is infeasible Final slack form to Laux having optimum objective value ‘ 0’. Thus our initial problem was feasible! 31 Linear Programming associated basic solution (4, 0, 0, 6, 0) which is feasible Pivoting

Formal Simplex Algorithm cont… Finding Initial solution [INITIALIZE-SIMPLEX (A, b, c)] cont… � Restoring the original objective function, (which is 2 x 1 - x 2 in our example) with appropriate substitutions, we get the objective function: � Setting x 0=0 and simplifying, we get the slack form This slack form has a feasible basic solution, and is returned by procedure INITIALIZE-SIMPLEX to procedure SIMPLEX. Feasible Basic Solution: (0, 4/5, 14/5, 0) 32 Linear Programming 21 -10 -2021

Formal Simplex Algorithm cont… Finding Initial solution [INITIALIZE-SIMPLEX (A, b, c)] cont… If the initial basic solution is feasible, algo. terminate here and return the corresponding slack form If the initial basic solution is not feasible, algo. Perform step 4 to 16 and return the corresponding slack form if exist or return infeasible otherwise 33 Linear Programming 21 -10 -2021

Formal Simplex Algorithm cont… Finding Initial solution [INITIALIZE-SIMPLEX (A, b, c)] cont… �Lemma 2 (correctness of INITIALIZE SIMPLEX): �If a linear program L has no feasible solution, then INITIALIZE-SIMPLEX returns “infeasible. ” Otherwise, it returns a valid slack form for which the basic solution is feasible. 34 Linear Programming 21 -10 -2021

Correctness of SIMPLEX (A, b, c) �To show that SIMPLEX works correctly, it is enough to show that: 1. If SIMPLEX has an initial feasible solution and eventually terminates, then it either returns a feasible solution or determines that the linear program is unbounded (Lemma 2 and 3). 2. Solution returned by SIMPLEX is optimal (Duality). 3. Algorithm terminate eventually. 35 Linear Programming 21 -10 -2021

RECALL: Formal Simplex Algorithm cont… initial basic feasible solution Return initial basic feasible solution. detects unbounded-ness Abbreviations N: indices set of nonbasic variables B: indices set of basic variables A: aij b: bi c: ci v: constant coefficient. e: index of entering variable l: index of leaving variable z=v+ j Ncjxj xi=bi- j Naijxj for i B optimal solution 36 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 1 � Lemma 3: Given a linear program (A, b, c), suppose that the call to INITIALIZE-SIMPLEX in line 1 of SIMPLEX returns a slack form for which the basic solution is feasible. Then if SIMPLEX returns a solution in line 16, that solution is a feasible solution to the linear program. If SIMPLEX returns “unbounded” in line 10, the linear program is unbounded. � Proof We use the following three-part loop invariant: At the start of each iteration of the while loop of lines 2– 11, 1. the slack form is equivalent to the slack form returned by the call of INITIALIZE-SIMPLEX, 2. for each i B, we have bi ≥ 0, and 3. the basic solution associated with the slack form is feasible. 37 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 1 Proof cont… � INITIALIZATION Invariant 1 The equivalence of the slack forms is trivial for the first iteration as it is output of INITIALIZE-SIMPLEX. Invariant 2 1. We are assuming basic solution to be feasible, 2. Thus, each basic variable xi is nonnegative. 3. Furthermore, since basic solution sets each basic variable xi to bi , 4. Thus by (2) and (3), we have bi ≥ 0 for all i B. Invariant 3 We assume, in the statement of the lemma, that the call to INITIALIZESIMPLEX in line 1 of SIMPLEX returns a slack form for which the basic solution is feasible. Thus, the third part of the invariant is true. 38 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 1 Proof cont… � MAINTENANCE Assuming that the return statement in line 10 does not execute. We shall handle the case when we discuss termination. Invariant 1 � Iteration of while loop has been changing one slack form into the another only by using the operation pivoting. � Thus the resultant slack form is equivalent to the one from the previous iteration which, by the loop invariant, is equivalent to the initial slack form. Invariant 2 � From the procedure SIMPLEX , it is clear that the change in the value of bi and set of basic variable B occur due to call to PIVOT in line 10. � Thus it is sufficient to show that, even after call to PIVOT, loop invariant holds. 39 Linear Programming 21 -10 -2021

Recall Pivot Simplex Algorithm Correctness Property 1 Proof cont… � MAINTENANCE Invariant 2 cont… � Now by line 2 of PIVOT, we have: Recall Simplex Since bi is nonnegative by loop invariant and ale is greater than 0 by line 5 of SIMPLEX. Thus, it is nonnegative. � For the remaining indices, we have: Two cases: If aie ≤ 0, aie > 0 Case 1: negative value of aie makes the result more nonnegative. 40 Linear Programming Case 2: By line 8 of simplex, we have So , we have

Simplex Algorithm Correctness Property 1 Proof cont… � MAINTENANCE Invariant 3 � The non-basic variables are set to 0 and thus are nonnegative. � Each basic variable xi is defined by the equation � The basic solution sets � Using the second part of the loop invariant, we know that b i ≥ 0 for all i B. . � Thus we conclude that each basic variable is nonnegative and hence solution is feasible. 41 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 1 Proof cont… � TERMINATION � The while loop can terminate in one of two ways. � It can terminates because of the condition in line 2, then the current basic solution is feasible and line 16 returns this solution. � It can terminates is by returning “un-bounded” in line 10. � Considering the second case, � we will find that line 10 executes only when line 9 is true. � Line 9 is true when line 5 is false. � Consider the basic solution We will now show that this is a feasible solution i. e. all variables are nonnegative. 42 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 1 Proof cont… TERMINATION � From the basic solution it is clear that, all non-basic variables are non-negative. � For each basic variables, we have All non basic variable other than entering one are 0 Now we have to show that objective value for this solution is unbounded: 43 positive It is 21 -10 -2021

Simplex Algorithm Correctness Property 2 –Duality[3] �Duality is used to show the optimality of solution. max becomes min Change x into y Given a program in standard form called primal linear program, corresponding dual program is built as: RHS coefficients swap places with objective function coefficients Change x into y Change the inequality sign 44 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 2 –Duality example 45 Linear Programming cont… Is the optimal value of the dual linear program is always equal to the optimal value of the primal linear program ? 21 -10 -2021

Simplex Algorithm Correctness Property 2 –Duality cont… Let us start with weak duality � Lemma 4 (Weak linear programming duality): Let be any feasible solution to the primal linear program and the dual linear program. Then, we have Proof: Recall by dual formulation Recall by standard form 46 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality cont… � Corollary 5: Let be any feasible solution to the primal linear program and the dual linear program. If we have then are optimal solution to the primal and linear program. 47 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality cont… Finding a dual solution whose value is equal to that of an optimal primal solution Suppose that the last slack form of the primal is: Then an optimum solution is to set We have i. e. objective value 48 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality cont… � Theorem 6 (Linear-programming duality) Suppose that SIMPLEX returns values for the primal linear program (A, b, c). Let N and B denote the nonbasic and basic variables for the final slack form, let c’ denote the coefficients in the final slack form, and let Then are the optimal solution to the primal linear and dual linear program resp, and (2). (1) 49 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality cont… Proof: � By Corollary 5, if we can find feasible solutions that satisfy must be optimal primal and part 2, of theorem, then dual solutions i. e. part 1 is satisfied. � Let us prove part 2 i. e. just show that the solutions described in the statement of theorem satisfy condition 2. � We have the last slack form of primal having objective function: Since SIMPLEX terminate with a solution. We have Bcz SIMPLEX runs till we have some ‘c’ coefficients with positive value 50 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality Proof cont… then Since all slack forms are equivalent, then the objective value of original and final slack form should be equal i. e Original objective function 51 Linear Programming Final slack form objective function 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality Proof cont… Thus we have Zero for non basic variable Assumed zero for basic variable Since all slack forms are equivalent, then equivalence of all slack forms implies that for any set of values x =(x 1, x 2, …, xn) , we have 52 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality Proof cont… Therefore for a particular set We have Recall By using 53 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality Proof cont… Apply Lemma 7 ( to be discussed next), we have 54 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality Proof cont… � To show that solution is feasible for dual program: � Since thus we have: It implies Recall and satisfying all constraints 55 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 2– Duality cont… � Lemma 7: • Lemma 8: Let (A, b, c) be a linear program in standard form. Given a set B of basic variables, the associated slack form is uniquely determined. 56 Linear Programming 21 -10 -2021

Simplex Algorithm Correctness Property 3 -Termination � It is always case that, each iteration of the simplex algorithm does not decreased the objective value associated with the basic solution. � But, it is possible that an iteration leaves the objective value unchanged. This phenomenon is called degeneracy. � Degeneracy leads to cycle. Lemma 9: If SIMPLEX fails to terminate in at most n+m. C iterations, then it cycles. m Lemma 10: If lines 3 and 8 of SIMPLEX always break ties by choosing the variable with the smallest index, then SIMPLEX must terminate. 57 Linear Programming 21 -10 -2021

Running time of Simplex � Lemma 11 �Assuming that INITIALIZE-SIMPLEX returns a slack form for which the basic solution is feasible, SIMPLEX either reports that a linear program is unbounded, or it terminates with a feasible solution in at most n+m. Cm iterations. � Proof: �We know that if INITIALIZE SIMPLEX returns a slack form for which the basic solution is feasible, then SIMPLEX either reports that a linear program is unbounded, or it terminates with a feasible solution. � By the contrapositive of Lemma 9, if SIMPLEX terminates with a feasible solution, then it terminates in at most n+m. Cm iterations. 58 Linear Programming 21 -10 -2021

Conclusion � Theorem 12 (Fundamental theorem of linear programming) Any linear program L, given in standard form, either 1. has an optimal solution with a finite objective value, 2. is infeasible, or 3. is unbounded. If L is infeasible, SIMPLEX returns “infeasible. ” If L is unbounded, SIMPLEX returns “unbounded. ” Otherwise, SIMPLEX returns an optimal solution with a finite objective value. 59 Linear Programming 21 -10 -2021

Thanks By: Kuldeep Kumar