Linear Programming Piyush Kumar Graphing 2 Dimensional LPs

Linear Programming Piyush Kumar

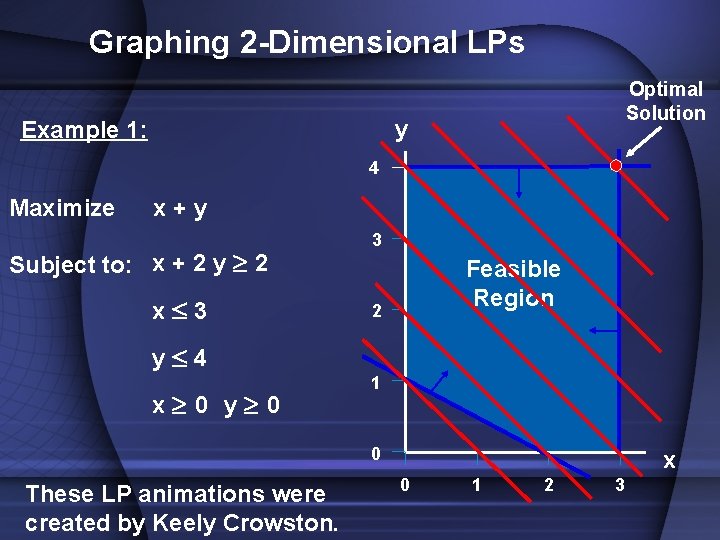
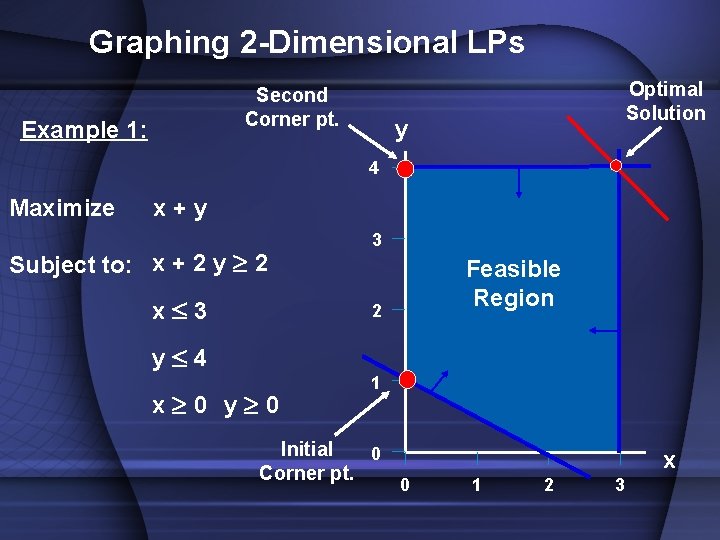
Graphing 2 -Dimensional LPs Optimal Solution y Example 1: 4 Maximize x+y Subject to: x + 2 y 2 x£ 3 y£ 4 x 0 y 0 3 Feasible Region 2 1 0 These LP animations were created by Keely Crowston. x 0 1 2 3

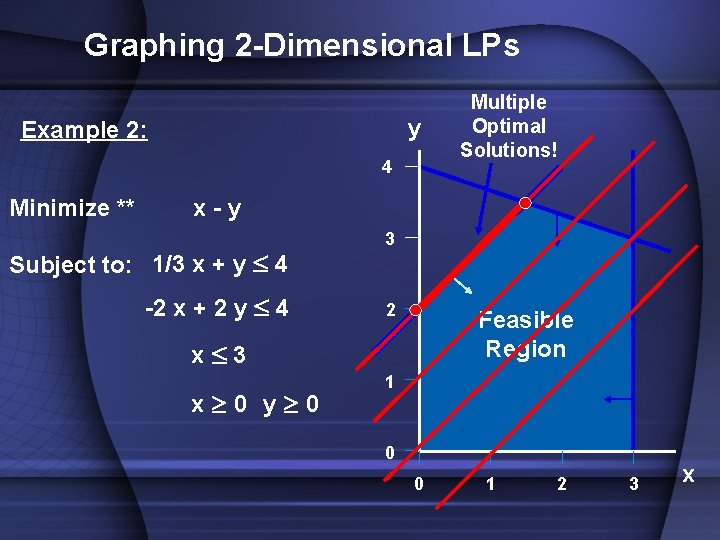
Graphing 2 -Dimensional LPs y Example 2: 4 Minimize ** Multiple Optimal Solutions! x-y Subject to: 1/3 x + y £ 4 -2 x + 2 y £ 4 3 2 Feasible Region x£ 3 x 0 y 0 1 0 0 1 2 3 x

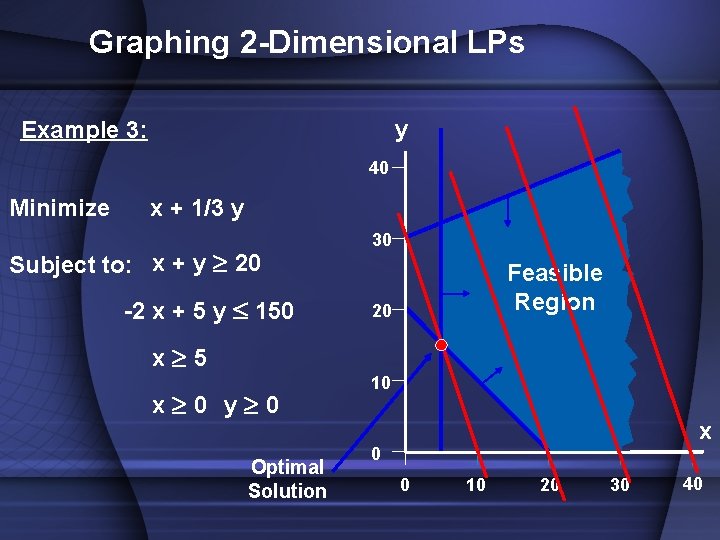
Graphing 2 -Dimensional LPs y Example 3: 40 Minimize x + 1/3 y Subject to: x + y 20 -2 x + 5 y £ 150 x 5 x 0 y 0 Optimal Solution 30 Feasible Region 20 10 x 0 0 10 20 30 40

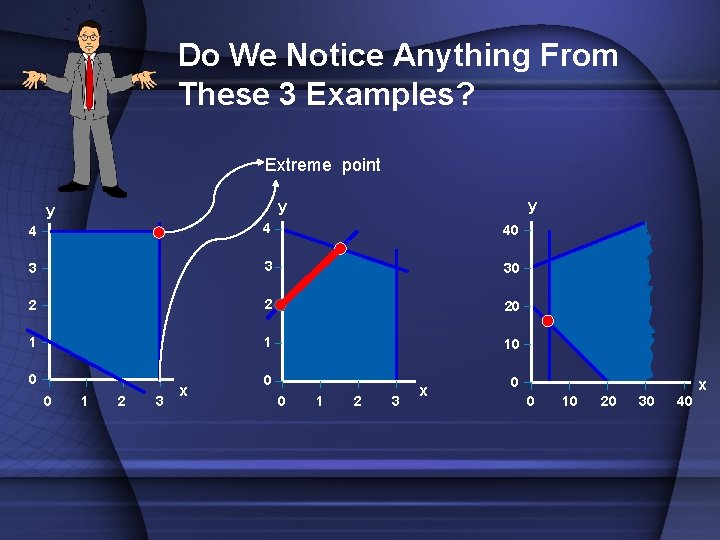
Do We Notice Anything From These 3 Examples? Extreme point y y y 4 4 40 3 3 30 2 2 20 1 1 10 0 0 1 2 3 x 0 0 10 20 x 30 40

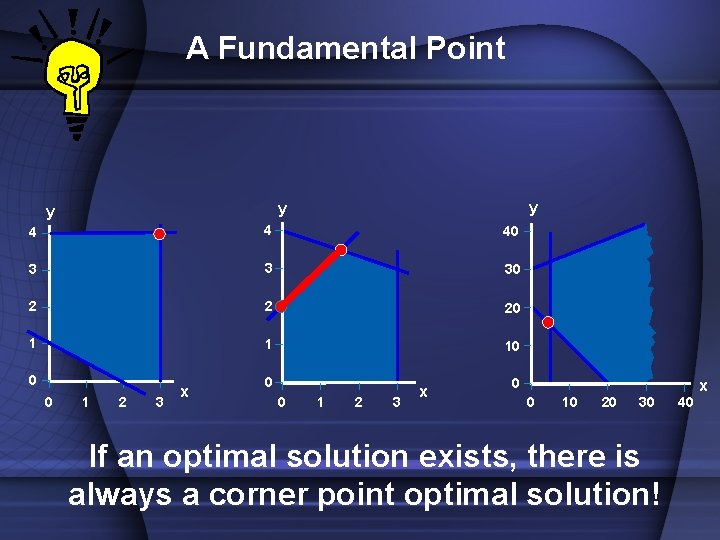
A Fundamental Point y y y 4 4 40 3 3 30 2 2 20 1 1 10 0 0 1 2 3 x 0 0 10 20 x 30 If an optimal solution exists, there is always a corner point optimal solution! 40

Graphing 2 -Dimensional LPs Second Corner pt. Example 1: Optimal Solution y 4 Maximize x+y Subject to: x + 2 y 2 x£ 3 3 Feasible Region 2 y£ 4 x 0 y 0 1 Initial 0 Corner pt. x 0 1 2 3

And We Can Extend this to Higher Dimensions

Then How Might We Solve an LP? o The constraints of an LP give rise to a geometrical shape - we call it a polyhedron. o If we can determine all the corner points of the polyhedron, then we can calculate the objective value at these points and take the best one as our optimal solution. o The Simplex Method intelligently moves from corner to corner until it can prove that it has found the optimal solution.

Linear Programs in higher dimensions maximize subject to z= -4 x 1 + x 2 - x 3 -7 x 1 + 5 x 2 + x 3 <= 8 -2 x 1 + 4 x 2 + 2 x 3 <= 10 x 1, x 2, x 3 0

In Matrix terms

LP Geometry Forms a d dimensional polyhedron Is convex : If z 1 and z 2 are two feasible solutions then λz 1+ (1 - λ)z 2 is also feasible. Extreme points can not be written as a convex combination of two feasible points.

LP Geometry Extreme point theorem: If there exists an optimal solution to an LP Problem, then there exists one extreme point where the optimum is achieved. Local optimum = Global Optimum

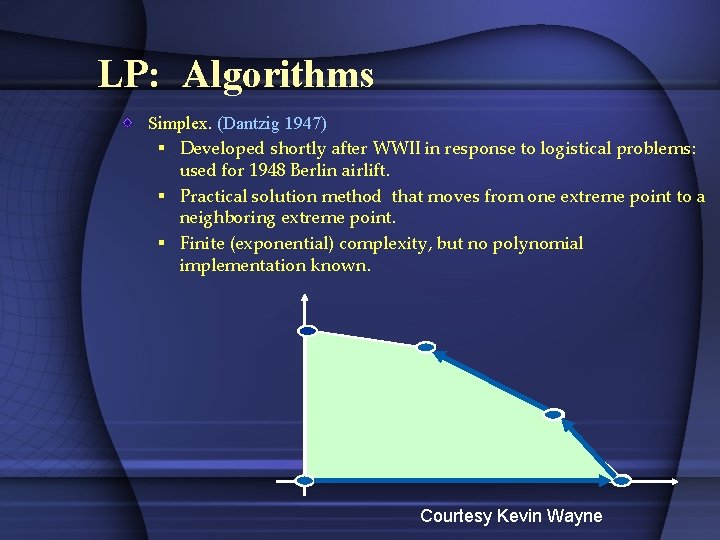
LP: Algorithms Simplex. (Dantzig 1947) § Developed shortly after WWII in response to logistical problems: used for 1948 Berlin airlift. § Practical solution method that moves from one extreme point to a neighboring extreme point. § Finite (exponential) complexity, but no polynomial implementation known. Courtesy Kevin Wayne

LP: Polynomial Algorithms Ellipsoid. (Khachian 1979, 1980) § Solvable in polynomial time: O(n 4 L) bit operations. o n = # variables o L = # bits in input § Theoretical tour de force. § Not remotely practical. Karmarkar's algorithm. (Karmarkar 1984) § O(n 3. 5 L). § Polynomial and reasonably efficient implementations possible. Interior point algorithms. § O(n 3 L). § Competitive with simplex! o Dominates on simplex for large problems. § Extends to even more general problems.

LP: The 2 D case Wlog, we can assume that c=(0, -1). So now we want to find the Extreme point with the smallest y coordinate. Lets also assume, no degeneracies, the solution is given by two Halfplanes intersecting at a point.

Incremental Algorithm? How would it work to solve a 2 D LP Problem? How much time would it take in the worst case? Can we do better?