Linear Programming Modeling Examples Chapter 4 Copyright 2010

Linear Programming: Modeling Examples Chapter 4 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -1

Chapter Topics n A Product Mix Example n A Diet Example n An Investment Example n A Marketing Example n A Transportation Example n A Blend Example n A Multiperiod Scheduling Example n A Data Envelopment Analysis Example Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -2

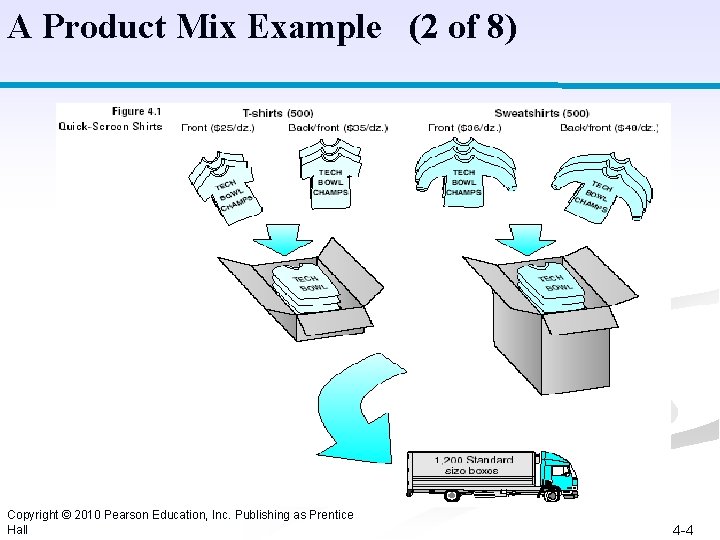
A Product Mix Example Problem Definition (1 of 8) Four-product T-shirt/sweatshirt manufacturing company. ■ Must complete production within 72 hours ■ Truck capacity = 1, 200 standard sized boxes. ■ Standard size box holds 12 T-shirts. ■ One-dozen sweatshirts box is three times size of standard box. ■ $25, 000 available for a production run. ■ 500 dozen blank T-shirts and sweatshirts in stock. ■ How many dozens (boxes) of each type of shirt to produce? Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -3

A Product Mix Example (2 of 8) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -4

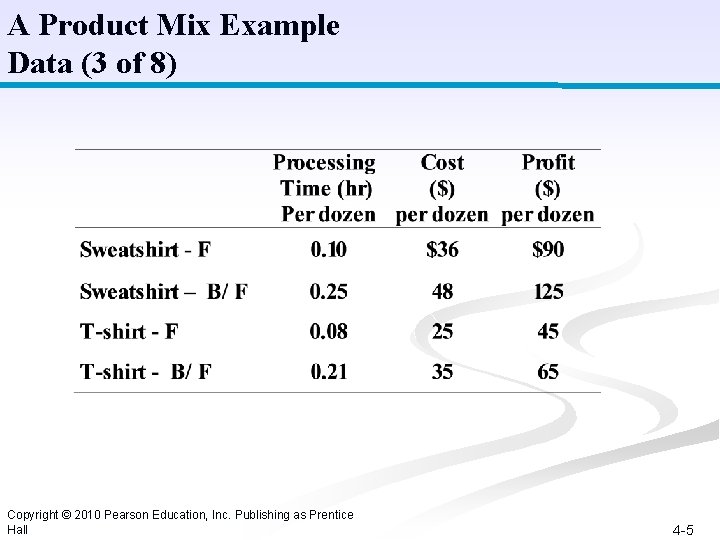
A Product Mix Example Data (3 of 8) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -5

A Product Mix Example Model Construction (4 of 8) Decision Variables: x 1 = sweatshirts, front printing x 2 = sweatshirts, back and front printing x 3 = T-shirts, front printing x 4 = T-shirts, back and front printing Objective Function: Maximize Z = $90 x 1 + $125 x 2 + $45 x 3 + $65 x 4 Model Constraints: 0. 10 x 1 + 0. 25 x 2+ 0. 08 x 3 + 0. 21 x 4 72 hr 3 x 1 + 3 x 2 + x 3 + x 4 1, 200 boxes $36 x 1 + $48 x 2 + $25 x 3 + $35 x 4 $25, 000 x 1 + x 2 500 dozen sweatshirts x 3 + x 4 500 dozen T-shirts Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -6

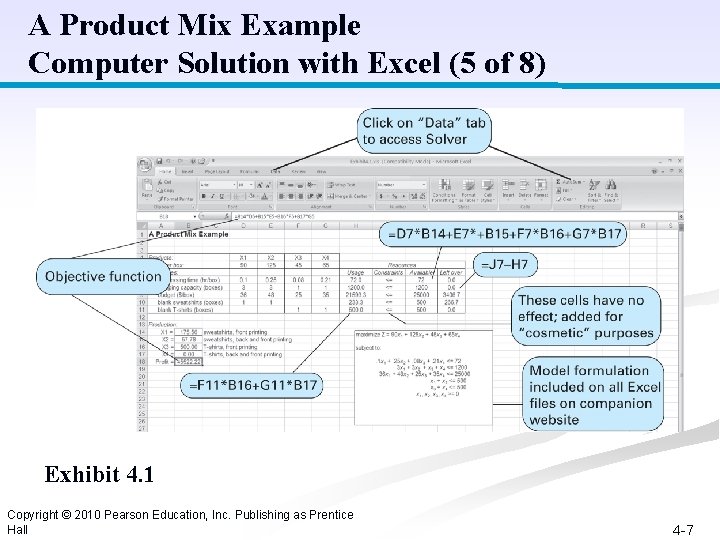
A Product Mix Example Computer Solution with Excel (5 of 8) Exhibit 4. 1 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -7

A Product Mix Example Solution with Excel Solver Window (6 of 8) Exhibit 4. 2 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -8

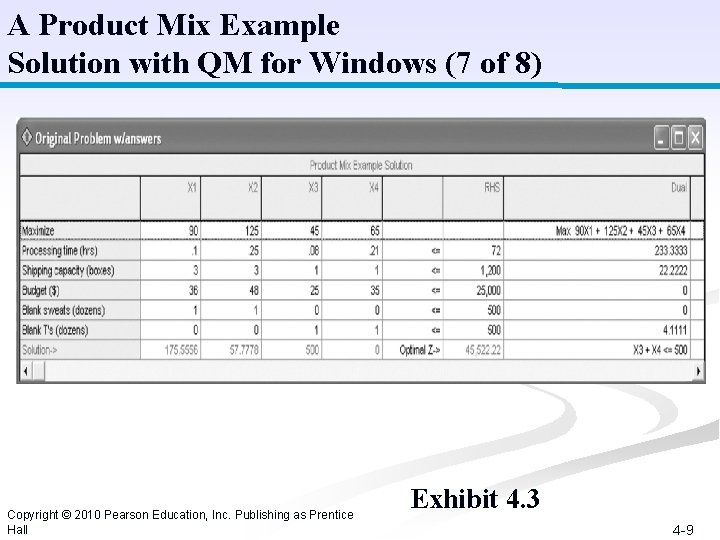
A Product Mix Example Solution with QM for Windows (7 of 8) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 3 4 -9

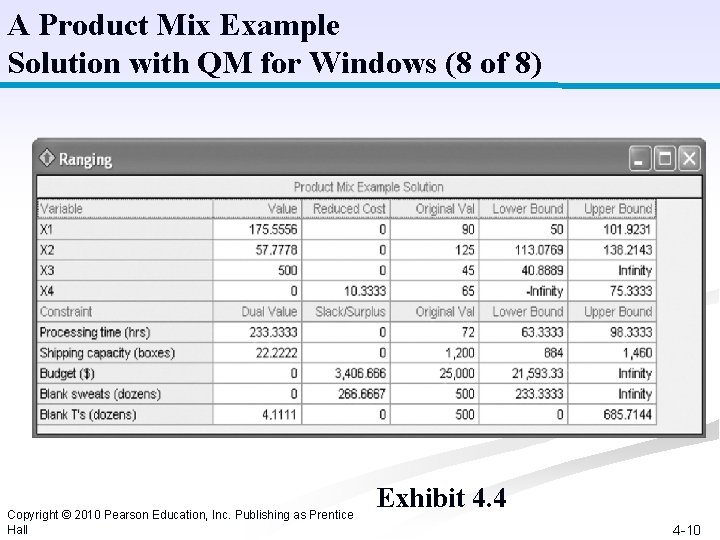
A Product Mix Example Solution with QM for Windows (8 of 8) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 4 4 -10

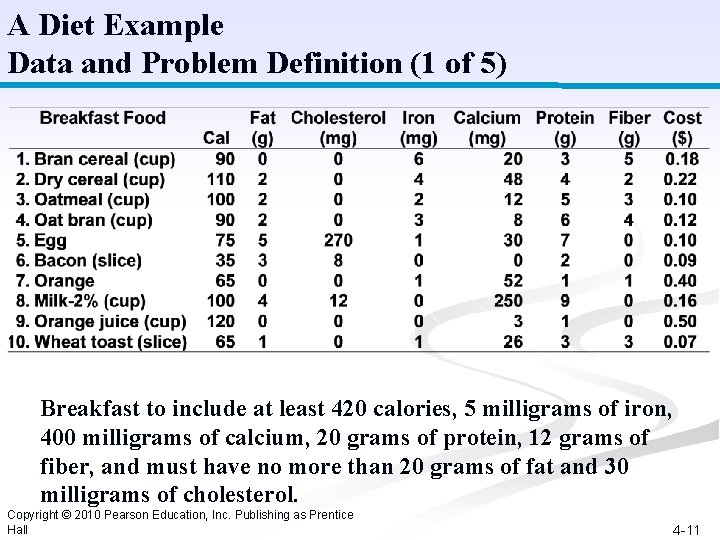
A Diet Example Data and Problem Definition (1 of 5) Breakfast to include at least 420 calories, 5 milligrams of iron, 400 milligrams of calcium, 20 grams of protein, 12 grams of fiber, and must have no more than 20 grams of fat and 30 milligrams of cholesterol. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -11

A Diet Example Model Construction – Decision Variables (2 of 5) x 1 = cups of bran cereal x 2 = cups of dry cereal x 3 = cups of oatmeal x 4 = cups of oat bran x 5 = eggs x 6 = slices of bacon x 7 = oranges x 8 = cups of milk x 9 = cups of orange juice x 10 = slices of wheat toast Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -12

A Diet Example Model Summary (3 of 5) Minimize Z = 0. 18 x 1 + 0. 22 x 2 + 0. 10 x 3 + 0. 12 x 4 + 0. 10 x 5 + 0. 09 x 6 + 0. 40 x 7 + 0. 16 x 8 + 0. 50 x 9 + 0. 07 x 10 subject to: 90 x 1 + 110 x 2 + 100 x 3 + 90 x 4 + 75 x 5 + 35 x 6 + 65 x 7 + 100 x 8 + 120 x 9 + 65 x 10 420 calories 2 x 2 + 2 x 3 + 2 x 4 + 5 x 5 + 3 x 6 + 4 x 8 + x 10 20 g fat 270 x 5 + 8 x 6 + 12 x 8 30 mg cholesterol 6 x 1 + 4 x 2 + 2 x 3 + 3 x 4+ x 5 + x 7 + x 10 5 mg iron 20 x 1 + 48 x 2 + 12 x 3 + 8 x 4+ 30 x 5 + 52 x 7 + 250 x 8 + 3 x 9 + 26 x 10 400 mg of calcium 3 x 1 + 4 x 2 + 5 x 3 + 6 x 4 + 7 x 5 + 2 x 6 + x 7 + 9 x 8+ x 9 + 3 x 10 20 g protein 5 x 1 + 2 x 2 + 3 x 3 + 4 x 4+ x 7 + 3 x 10 12 xi 0, for all j Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -13

A Diet Example Computer Solution with Excel (4 of 5) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 5 4 -14

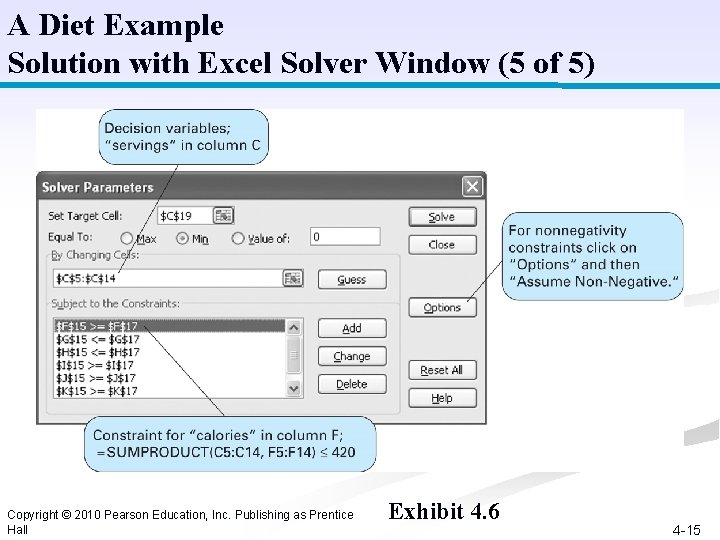
A Diet Example Solution with Excel Solver Window (5 of 5) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 6 4 -15

An Investment Example Model Summary (1 of 4) Maximize Z = $0. 085 x 1 + 0. 05 x 2 + 0. 065 x 3+ 0. 130 x 4 subject to: x 1 $14, 000 x 2 - x 1 - x 3 - x 4 0 x 2 + x 3 $21, 000 -1. 2 x 1 + x 2 + x 3 - 1. 2 x 4 0 x 1 + x 2 + x 3 + x 4 = $70, 000 x 1, x 2, x 3, x 4 0 where x 1 = amount ($) invested in municipal bonds x 2 = amount ($) invested in certificates of deposit x 3 = amount ($) invested in treasury bills x 4 = amount ($) invested in growth stock fund Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -16

An Investment Example Computer Solution with Excel (2 of 4) Exhibit 4. 7 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -17

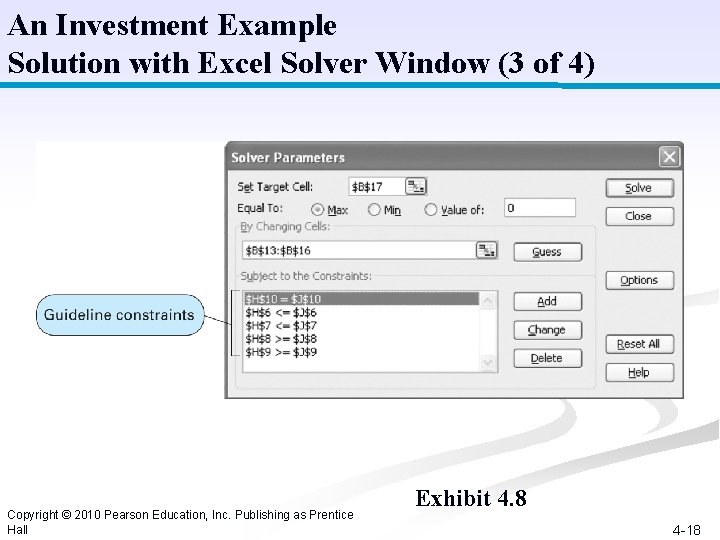
An Investment Example Solution with Excel Solver Window (3 of 4) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 8 4 -18

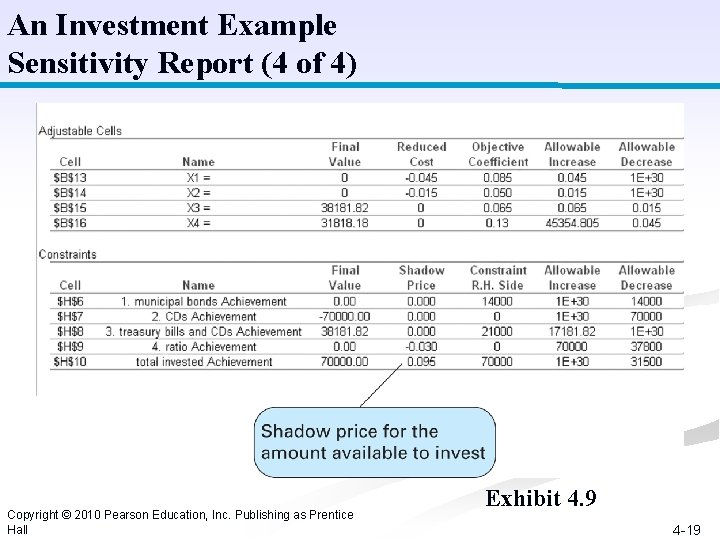
An Investment Example Sensitivity Report (4 of 4) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 9 4 -19

A Marketing Example Data and Problem Definition (1 of 6) § Budget limit $100, 000 § Television time for four commercials § Radio time for 10 commercials § Newspaper space for 7 ads § Resources for no more than 15 commercials and/or ads Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -20

A Marketing Example Model Summary (2 of 6) Maximize Z = 20, 000 x 1 + 12, 000 x 2 + 9, 000 x 3 subject to: 15, 000 x 1 + 6, 000 x 2+ 4, 000 x 3 100, 000 x 1 4 x 2 10 x 3 7 x 1 + x 2 + x 3 15 x 1, x 2, x 3 0 where x 1 = number of television commercials x 2 = number of radio commercials x 3 = number of newspaper ads Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -21

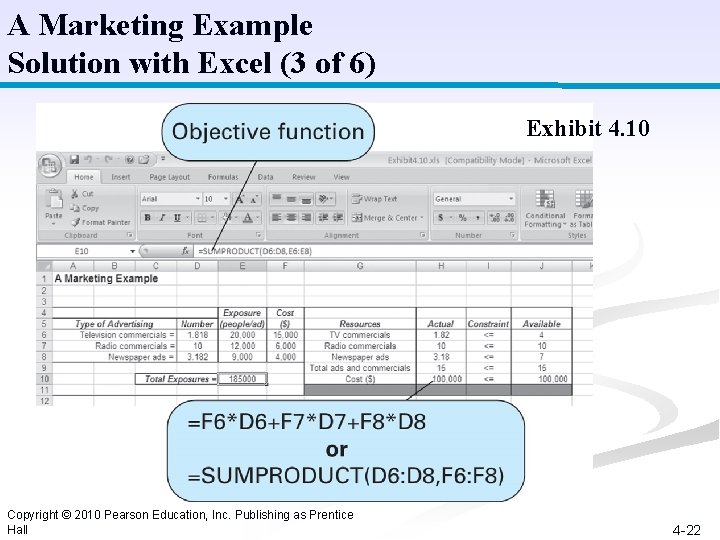
A Marketing Example Solution with Excel (3 of 6) Exhibit 4. 10 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -22

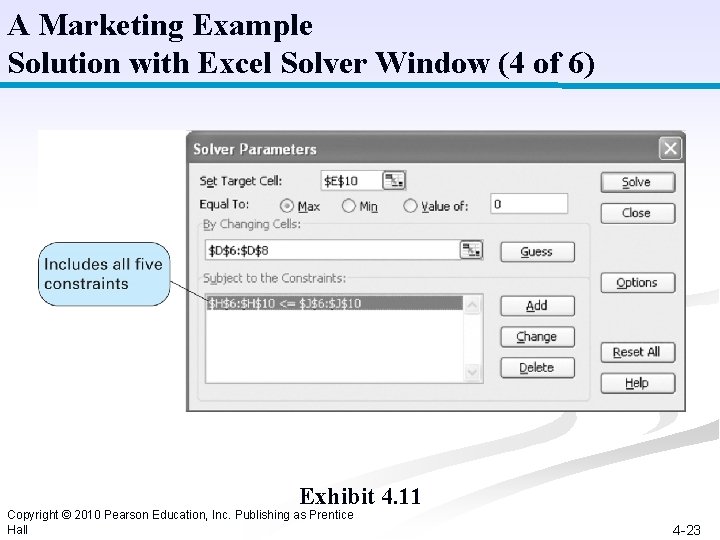
A Marketing Example Solution with Excel Solver Window (4 of 6) Exhibit 4. 11 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -23

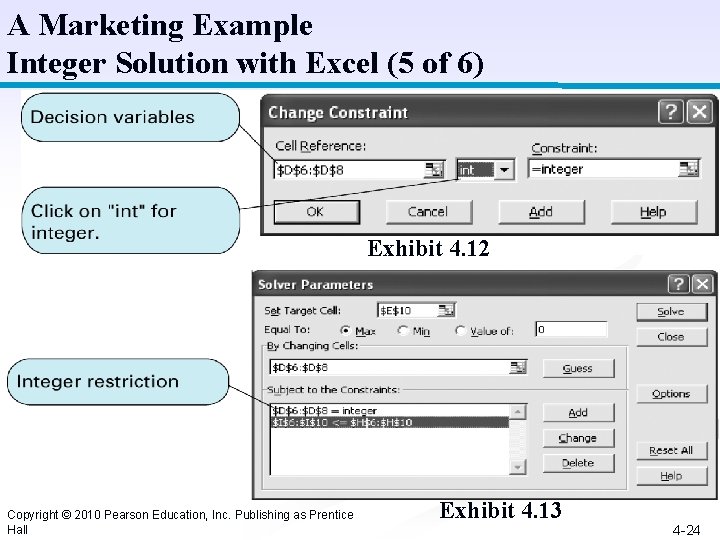
A Marketing Example Integer Solution with Excel (5 of 6) Exhibit 4. 12 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 13 4 -24

A Marketing Example Integer Solution with Excel (6 of 6) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 14 4 -25

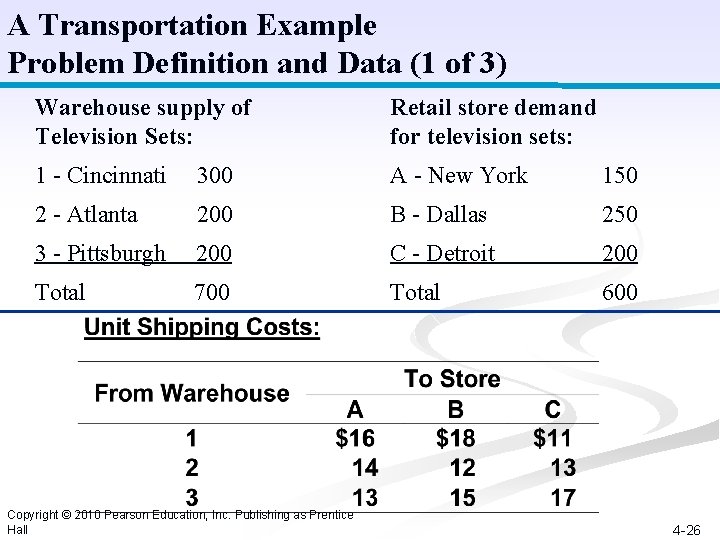
A Transportation Example Problem Definition and Data (1 of 3) Warehouse supply of Television Sets: Retail store demand for television sets: 1 - Cincinnati 300 A - New York 150 2 - Atlanta 200 B - Dallas 250 3 - Pittsburgh 200 C - Detroit 200 Total 700 Total 600 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -26

A Transportation Example Model Summary (2 of 4) Minimize Z = $16 x 1 A + 18 x 1 B + 11 x 1 C + 14 x 2 A + 12 x 2 B + 13 x 2 C + 13 x 3 A + 15 x 3 B + 17 x 3 C subject to: x 1 A + x 1 B+ x 1 C 300 x 2 A+ x 2 B + x 2 C 200 x 3 A+ x 3 B + x 3 C 200 x 1 A + x 2 A + x 3 A = 150 x 1 B + x 2 B + x 3 B = 250 x 1 C + x 2 C + x 3 C = 200 All xij 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -27

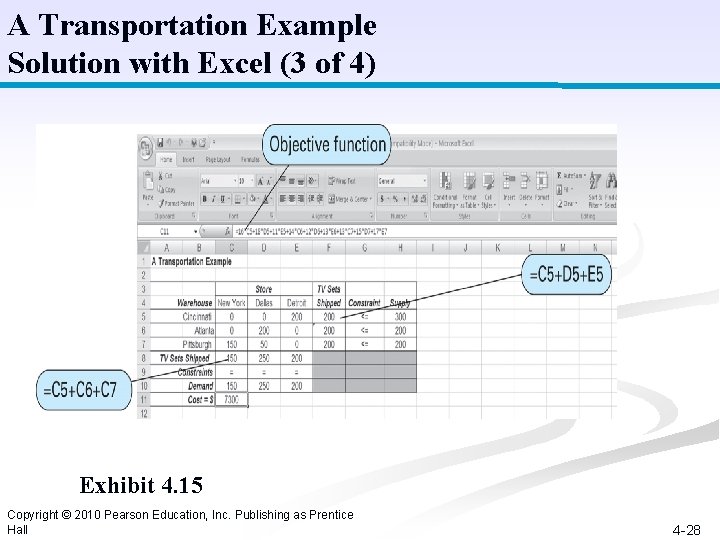
A Transportation Example Solution with Excel (3 of 4) Exhibit 4. 15 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -28

A Transportation Example Solution with Solver Window (4 of 4) Exhibit 4. 16 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -29

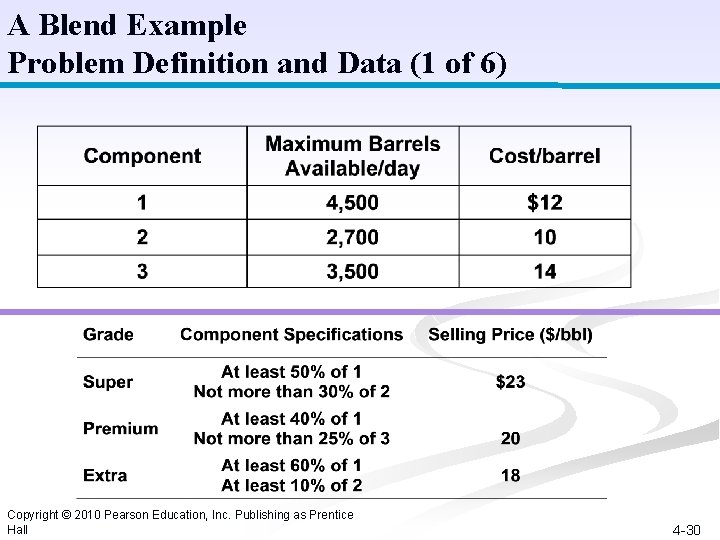
A Blend Example Problem Definition and Data (1 of 6) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -30

A Blend Example Problem Statement and Variables (2 of 6) ■ Determine the optimal mix of the three components in each grade of motor oil that will maximize profit. Company wants to produce at least 3, 000 barrels of each grade of motor oil. ■ Decision variables: The quantity of each of the three components used in each grade of gasoline (9 decision variables); xij = barrels of component i used in motor oil grade j per day, where i = 1, 2, 3 and j = s (super), p (premium), and e (extra). Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -31

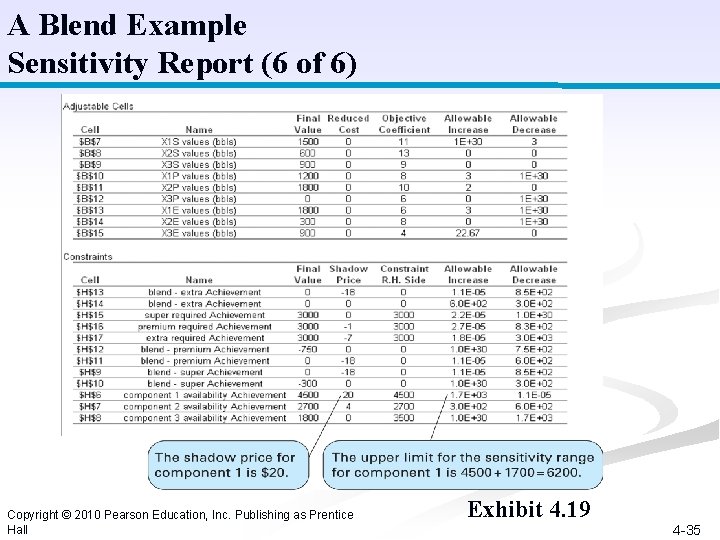
A Blend Example Model Summary (3 of 6) Maximize Z = 11 x 1 s + 13 x 2 s + 9 x 3 s + 8 x 1 p + 10 x 2 p + 6 x 3 p + 6 x 1 e + 8 x 2 e + 4 x 3 e subject to: x 1 s + x 1 p + x 1 e 4, 500 bbl. x 2 s + x 2 p + x 2 e 2, 700 bbl. x 3 s + x 3 p + x 3 e 3, 500 bbl. 0. 50 x 1 s - 0. 50 x 2 s - 0. 50 x 3 s 0 0. 70 x 2 s - 0. 30 x 1 s - 0. 30 x 3 s 0 0. 60 x 1 p - 0. 40 x 2 p - 0. 40 x 3 p 0 0. 75 x 3 p - 0. 25 x 1 p - 0. 25 x 2 p 0 0. 40 x 1 e- 0. 60 x 2 e- - 0. 60 x 3 e 0 0. 90 x 2 e - 0. 10 x 1 e - 0. 10 x 3 e 0 x 1 s + x 2 s + x 3 s 3, 000 bbl. x 1 p+ x 2 p + x 3 p 3, 000 bbl. all xij 0 x 1 e+ x 2 e + x 3 e 3, 000 bbl. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -32

A Blend Example Solution with Excel (4 of 6) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 17 4 -33

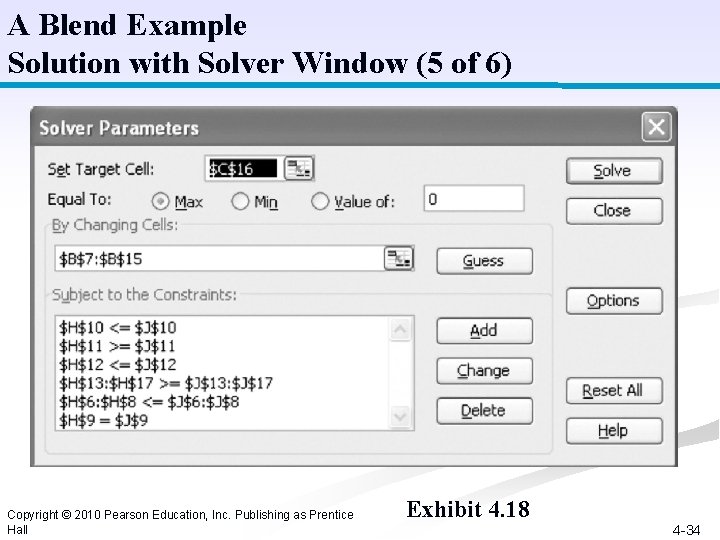
A Blend Example Solution with Solver Window (5 of 6) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 18 4 -34

A Blend Example Sensitivity Report (6 of 6) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 19 4 -35

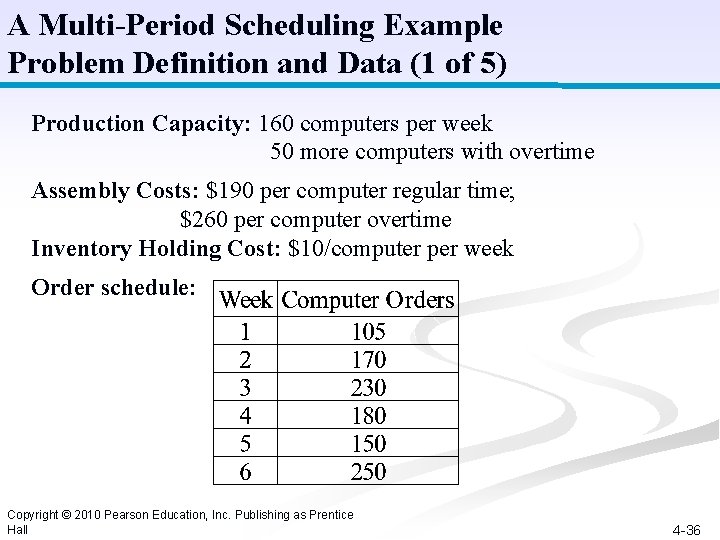
A Multi-Period Scheduling Example Problem Definition and Data (1 of 5) Production Capacity: 160 computers per week 50 more computers with overtime Assembly Costs: $190 per computer regular time; $260 per computer overtime Inventory Holding Cost: $10/computer per week Order schedule: Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -36

A Multi-Period Scheduling Example Decision Variables (2 of 5) Decision Variables: rj = regular production of computers in week j (j = 1, 2, …, 6) oj = overtime production of computers in week j (j = 1, 2, …, 6) ij = extra computers carried over as inventory in week j (j = 1, 2, …, 5) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -37

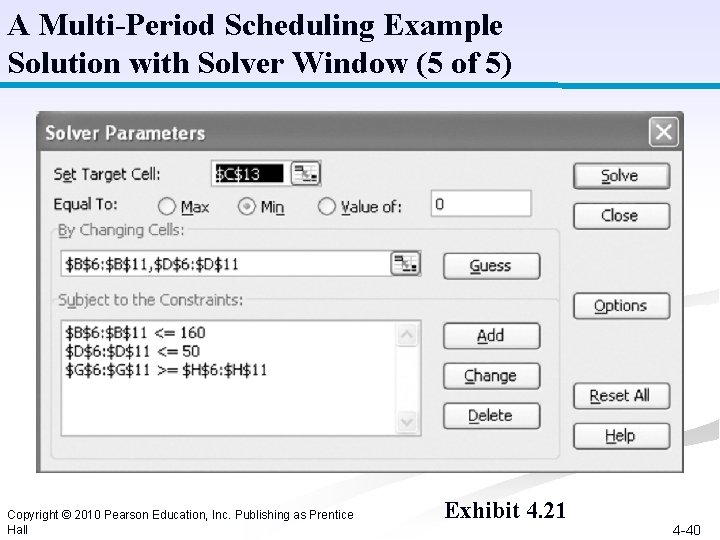
A Multi-Period Scheduling Example Model Summary (3 of 5) Model summary: Minimize Z = $190(r 1 + r 2 + r 3 + r 4 + r 5 + r 6) + $260(o 1+o 2 +o 3 +o 4+o 5+o 6) + 10(i 1 + i 2 + i 3 + i 4 + i 5) subject to: rj 160 computers in week j (j = 1, 2, 3, 4, 5, 6) oj 150 computers in week j (j = 1, 2, 3, 4, 5, 6) r 1 + o 1 - i 1 = 105 week 1 r 2 + o 2 + i 1 - i 2 = 170 week 2 r 3 + o 3 + i 2 - i 3 = 230 week 3 r 4 + o 4 + i 3 - i 4 = 180 week 4 r 5 + o 5 + i 4 - i 5 = 150 week 5 r 6 + o 6 + i 5 = 250 week 6 rj, oj, ij 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -38

A Multi-Period Scheduling Example Solution with Excel (4 of 5) Exhibit 4. 20 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -39

A Multi-Period Scheduling Example Solution with Solver Window (5 of 5) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 21 4 -40

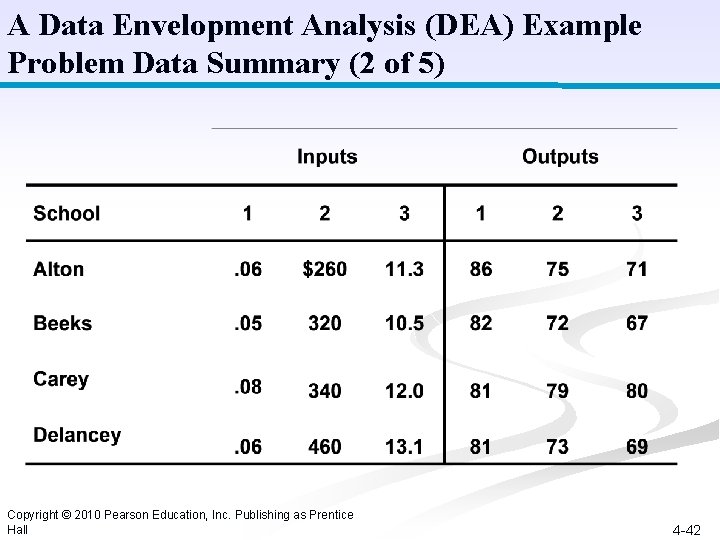
A Data Envelopment Analysis (DEA) Example Problem Definition (1 of 5) DEA compares a number of service units of the same type based on their inputs (resources) and outputs. The result indicates if a particular unit is less productive, or efficient, than other units. Elementary school comparison: Input 1 = teacher to student ratio Input 2 = supplementary funds/student Input 3 = average educational level of parents Output 1 = average reading SOL score Output 2 = average math SOL score Output 3 = average history SOL score Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -41

A Data Envelopment Analysis (DEA) Example Problem Data Summary (2 of 5) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -42

A Data Envelopment Analysis (DEA) Example Decision Variables and Model Summary (3 of 5) Decision Variables: xi = a price per unit of each output where i = 1, 2, 3 yi = a price per unit of each input where i = 1, 2, 3 Model Summary: Maximize Z = 81 x 1 + 73 x 2 + 69 x 3 subject to: . 06 y 1 + 460 y 2 + 13. 1 y 3 = 1 86 x 1 + 75 x 2 + 71 x 3 . 06 y 1 + 260 y 2 + 11. 3 y 3 82 x 1 + 72 x 2 + 67 x 3 . 05 y 1 + 320 y 2 + 10. 5 y 3 81 x 1 + 79 x 2 + 80 x 3 . 08 y 1 + 340 y 2 + 12. 0 y 3 81 x 1 + 73 x 2 + 69 x 3 . 06 y 1 + 460 y 2 + 13. 1 y 3 xi, yi 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -43

A Data Envelopment Analysis (DEA) Example Solution with Excel (4 of 5) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 22 4 -44

A Data Envelopment Analysis (DEA) Example Solution with Solver Window (5 of 5) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 23 4 -45

Example Problem Solution Problem Statement and Data (1 of 5) Canned cat food, Meow Chow; dog food, Bow Chow. ■ Ingredients/week: 600 lb horse meat; 800 lb fish; 1000 lb cereal. ■ Recipe requirement: Meow Chow at least half fish Bow Chow at least half horse meat. ■ 2, 250 sixteen-ounce cans available each week. ■ Profit /can: Meow Chow $0. 80 Bow Chow $0. 96. How many cans of Bow Chow and Meow Chow should be produced each week in order to maximize profit? Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -46

Example Problem Solution Model Formulation (2 of 5) Step 1: Define the Decision Variables xij = ounces of ingredient i in pet food j per week, where i = h (horse meat), f (fish) and c (cereal), and j = m (Meow chow) and b (Bow Chow). Step 2: Formulate the Objective Function Maximize Z = $0. 05(xhm + xfm + xcm) + 0. 06(xhb + xfb + xcb) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -47

Example Problem Solution Model Formulation (3 of 5) Step 3: Formulate the Model Constraints Amount of each ingredient available each week: xhm + xhb 9, 600 ounces of horse meat xfm + xfb 12, 800 ounces of fish xcm + xcb 16, 000 ounces of cereal additive Recipe requirements: Meow Chow: xfm/(xhm + xfm + xcm) 1/2 or - xhm + xfm- xcm 0 Bow Chow: xhb/(xhb + xfb + xcb) 1/2 or xhb- xfb - xcb 0 Can Content: xhm + xfm + xcm + xhb + xfb+ xcb 36, 000 ounces Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -48

Example Problem Solution Model Summary (4 of 5) Step 4: Model Summary Maximize Z = $0. 05 xhm + $0. 05 xfm + $0. 05 xcm + $0. 06 xhb + 0. 06 xfb + 0. 06 xcb subject to: xhm + xhb 9, 600 ounces of horse meat xfm + xfb 12, 800 ounces of fish xcm + xcb 16, 000 ounces of cereal additive - xhm + xfm- xcm 0 xhb- xfb - xcb 0 xhm + xfm + xcm + xhb + xfb+ xcb 36, 000 ounces xij 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -49

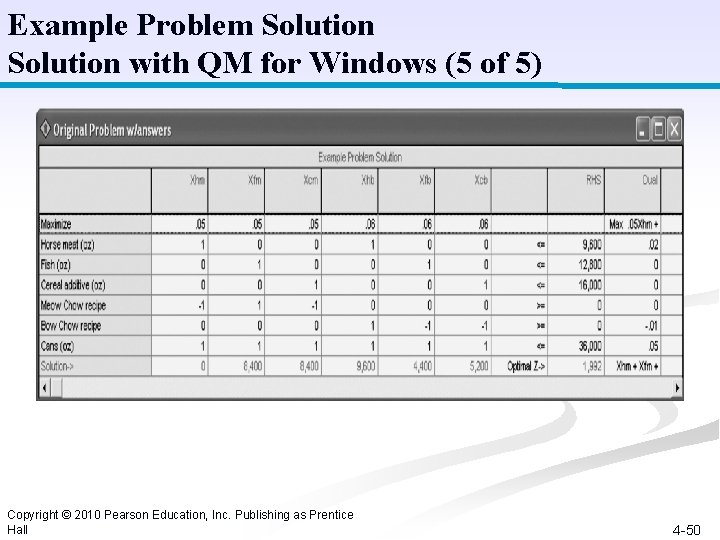
Example Problem Solution with QM for Windows (5 of 5) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -50

Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -51