Linear Programming Modeling Examples Chapter 4 Copyright 2010

Linear Programming: Modeling Examples Chapter 4 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -1

Chapter Topics n A Product Mix Example n A Diet Example n An Investment Example n A Marketing Example n A Transportation Example n A Blend Example n A Multiperiod Scheduling Example Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -2

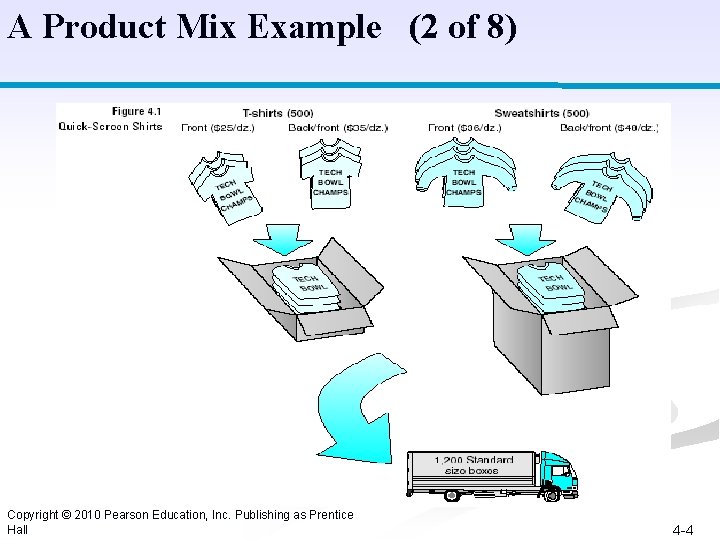
A Product Mix Example Problem Definition (1 of 8) T-shirt/Sweatshirt manufacturing company. ■ Must complete production within 72 hours ■ Truck capacity is 1, 200 standard sized-boxes. Standard size box holds 12 T-shirts. A 12 -sweatshirt box is three times the size of a standard box. ■ $25, 000 available for a production run. ■ There are 500 dozen blank sweatshirts and 500 dozen blank Tshirts in stock. ■ How many dozens (boxes) of each type of shirt to produce? ■ Sweatshirt with Front Print ■ Sweatshirt with Front and Back Print ■ T-shirt with Front and Back Print 4 -3

A Product Mix Example (2 of 8) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -4

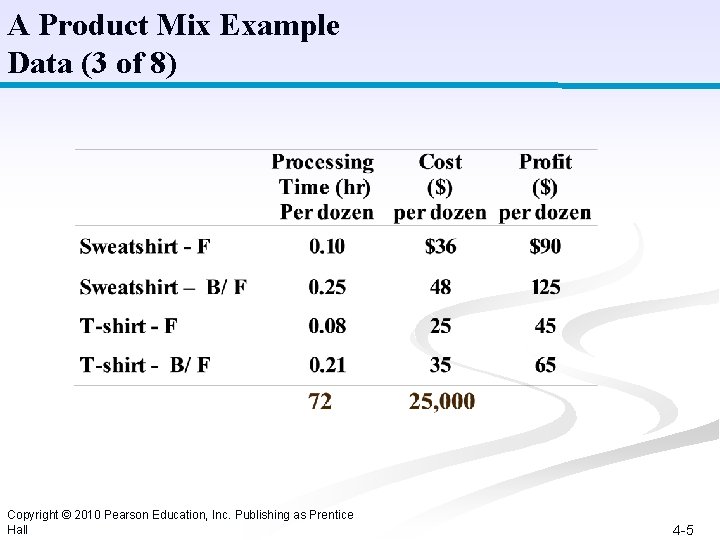
A Product Mix Example Data (3 of 8) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -5

A Product Mix Example Model Construction (4 of 8) Decision Variables: x 1 = sweatshirts, front printing x 2 = sweatshirts, back and front printing x 3 = T-shirts, front printing x 4 = T-shirts, back and front printing Objective Function: Maximize Z = $90 x 1 + $125 x 2 + $45 x 3 + $65 x 4 Model Constraints: 0. 10 x 1 + 0. 25 x 2+ 0. 08 x 3 + 0. 21 x 4 72 hr 3 x 1 + 3 x 2 + x 3 + x 4 1, 200 boxes $36 x 1 + $48 x 2 + $25 x 3 + $35 x 4 $25, 000 x 1 + x 2 500 dozen sweatshirts x 3 + x 4 500 dozen T-shirts Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -6

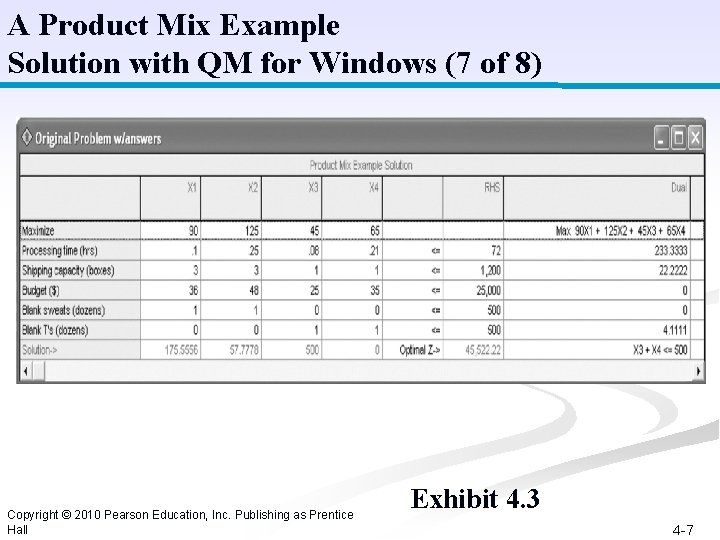
A Product Mix Example Solution with QM for Windows (7 of 8) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 3 4 -7

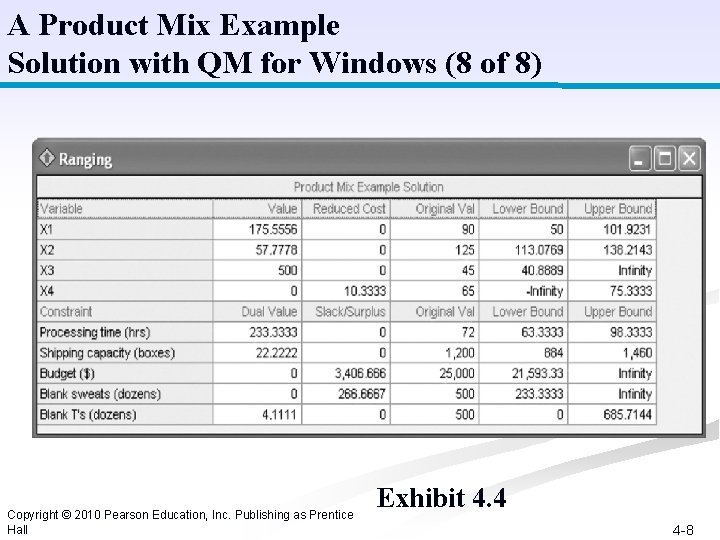
A Product Mix Example Solution with QM for Windows (8 of 8) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall Exhibit 4. 4 4 -8

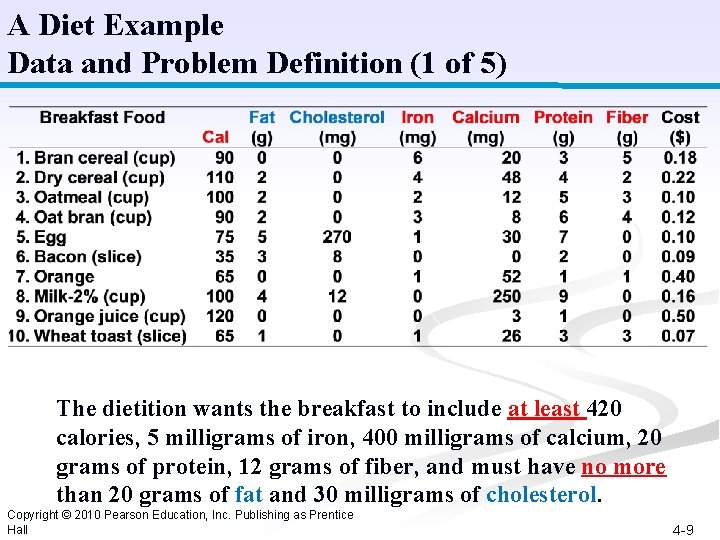
A Diet Example Data and Problem Definition (1 of 5) The dietition wants the breakfast to include at least 420 calories, 5 milligrams of iron, 400 milligrams of calcium, 20 grams of protein, 12 grams of fiber, and must have no more than 20 grams of fat and 30 milligrams of cholesterol. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -9

A Diet Example Model Construction – Decision Variables (2 of 5) x 1 = cups of bran cereal x 2 = cups of dry cereal x 3 = cups of oatmeal x 4 = cups of oat bran x 5 = eggs x 6 = slices of bacon x 7 = oranges x 8 = cups of milk x 9 = cups of orange juice x 10 = slices of wheat toast Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -10

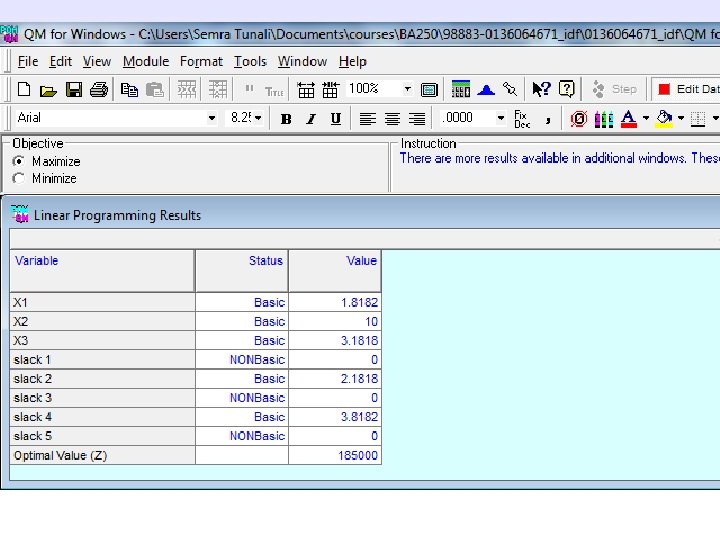
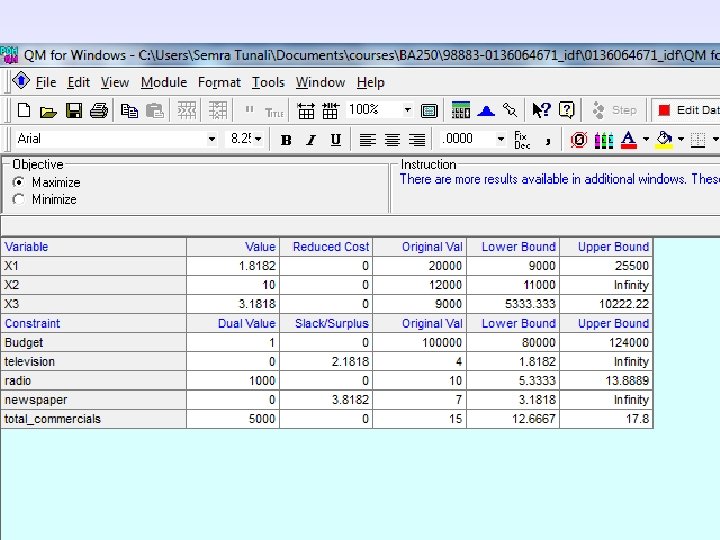
A Diet Example Model Summary (3 of 5) Minimize Z = 0. 18 x 1 + 0. 22 x 2 + 0. 10 x 3 + 0. 12 x 4 + 0. 10 x 5 + 0. 09 x 6 + 0. 40 x 7 + 0. 16 x 8 + 0. 50 x 9 + 0. 07 x 10 subject to: 90 x 1 + 110 x 2 + 100 x 3 + 90 x 4 + 75 x 5 + 35 x 6 + 65 x 7 + 100 x 8 + 120 x 9 + 65 x 10 420 calories 2 x 2 + 2 x 3 + 2 x 4 + 5 x 5 + 3 x 6 + 4 x 8 + x 10 20 g fat 270 x 5 + 8 x 6 + 12 x 8 30 mg cholesterol 6 x 1 + 4 x 2 + 2 x 3 + 3 x 4+ x 5 + x 7 + x 10 5 mg iron 20 x 1 + 48 x 2 + 12 x 3 + 8 x 4+ 30 x 5 + 52 x 7 + 250 x 8 + 3 x 9 + 26 x 10 400 mg of calcium 3 x 1 + 4 x 2 + 5 x 3 + 6 x 4 + 7 x 5 + 2 x 6 + x 7 + 9 x 8+ x 9 + 3 x 10 20 g protein 5 x 1 + 2 x 2 + 3 x 3 + 4 x 4+ x 7 + 3 x 10 12 g fiber xi 0, for all j Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -11

OPTIMUM SOLUTION X 3 = 1. 025 cups of outmeal n X 8 = 1. 241 cups of milk n X 10 = 2. 975 slices of wheat tost n (Cost) Z = $0. 509 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -12

An Investment Example $70, 000 (All of it) to divide between several investments • Municipal bonds – 8. 5% annual return • Certificates of deposit – 5% • Treasury bills – 6. 5% • Growth stock fund – 13% - No more than 20% of investment should be in Municipal Bonds - The amount invested in deposit cannot exceed the amount invested in the other three alternatives. - At least 30% in treasury bills and deposit - Amount invested in deposits and treasury bills should be no less than in bonds and stock funds; the ratio should be at least 1. 2 to 1. 4 -13

How much to invest in each alternative to maximize the return? ? ? Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -14

An Investment Example Model Summary (1 of 4) Maximize Z = $0. 085 x 1 + 0. 05 x 2 + 0. 065 x 3+ 0. 130 x 4 subject to: x 1 $14, 000 x 2 - x 1 - x 3 - x 4 0 x 2 + x 3 $21, 000 -1. 2 x 1 + x 2 + x 3 - 1. 2 x 4 0 x 1 + x 2 + x 3 + x 4 = $70, 000 x 1, x 2, x 3, x 4 0 where x 1 = amount ($) invested in municipal bonds x 2 = amount ($) invested in certificates of deposit x 3 = amount ($) invested in treasury bills x 4 = amount ($) invested in growth stock fund Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -15

An Investment Example n What if we change the constraint defining the entire amount of fund to invest as follows? x 1 + x 2 + x 3 + x 4 <= $70000 What changes to be made to the LP model ? ? ? Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -16

Maximize Z = $0. 085 x 1 + 0. 05 x 2 + 0. 065 x 3+ 0. 130 x 4 subject to: x 1 $14, 000 x 2 - x 1 - x 3 - x 4 0 x 2 + x 3 $21, 000 -1. 2 x 1 + x 2 + x 3 - 1. 2 x 4 0 x 1 + x 2 + x 3 + x 4 = $70, 000 x 1, x 2, x 3, x 4 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -17

A Marketing Example (The Biggs Dept. Store Chain hires an advertising firm) § Budget limit $100, 000 § Television station has time available for 4 commercials § Radio station has time for 10 commercials § Newspaper has space for 7 ads § Resources available for no more than 15 commercials and/or ads Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -18

A Marketing Example Maximize Z = 20, 000 x 1 + 12, 000 x 2 + 9, 000 x 3 subject to: 15, 000 x 1 + 6, 000 x 2+ 4, 000 x 3 100, 000 x 1 4 x 2 10 x 3 7 x 1 + x 2 + x 3 15 x 1, x 2, x 3 0 where x 1 = number of television commercials x 2 = number of radio commercials x 3 = number of newspaper ads Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -19

Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -20

Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -21

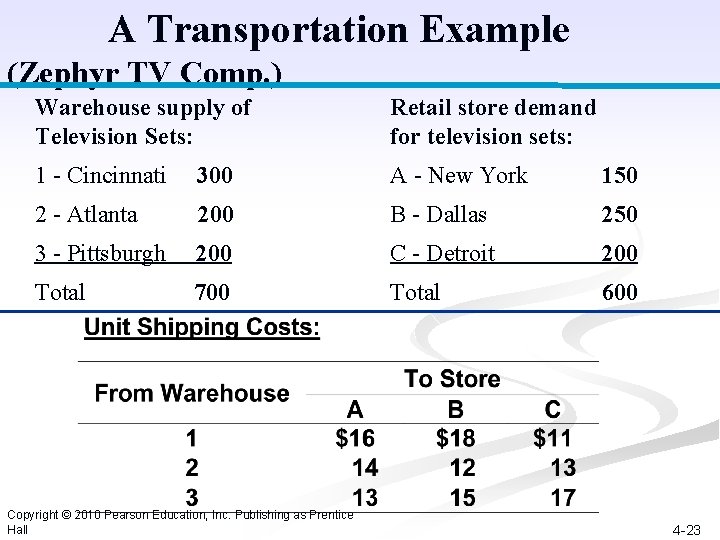
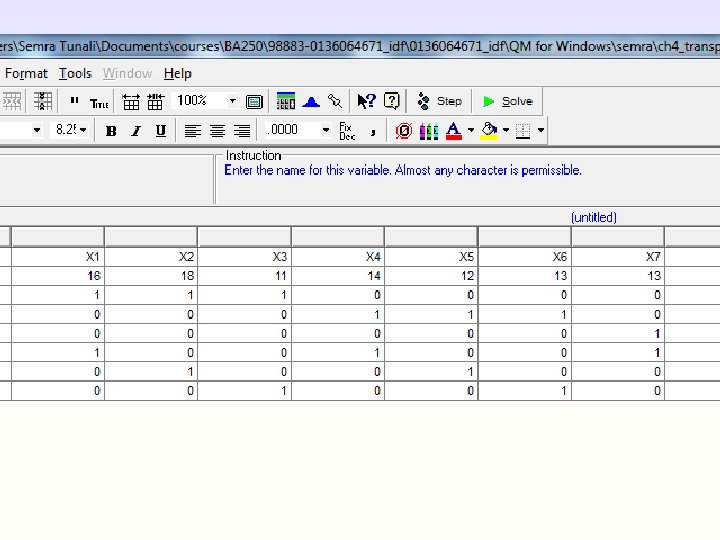
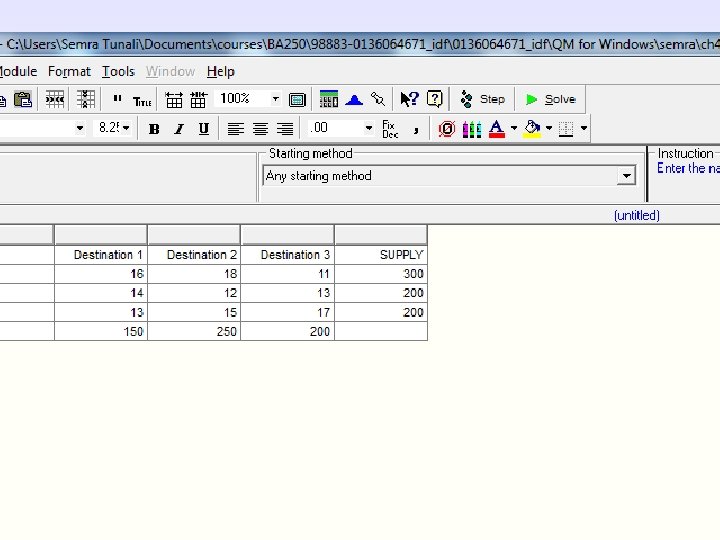
A Transportation Example n The Zephyr Television Company ships televisions from three warehouses to three retail stores on a monthly basis. n Each warehouse has a fixed supply per month, and each store has a fixed demand per month. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -22

A Transportation Example (Zephyr TV Comp. ) Warehouse supply of Television Sets: Retail store demand for television sets: 1 - Cincinnati 300 A - New York 150 2 - Atlanta 200 B - Dallas 250 3 - Pittsburgh 200 C - Detroit 200 Total 700 Total 600 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -23

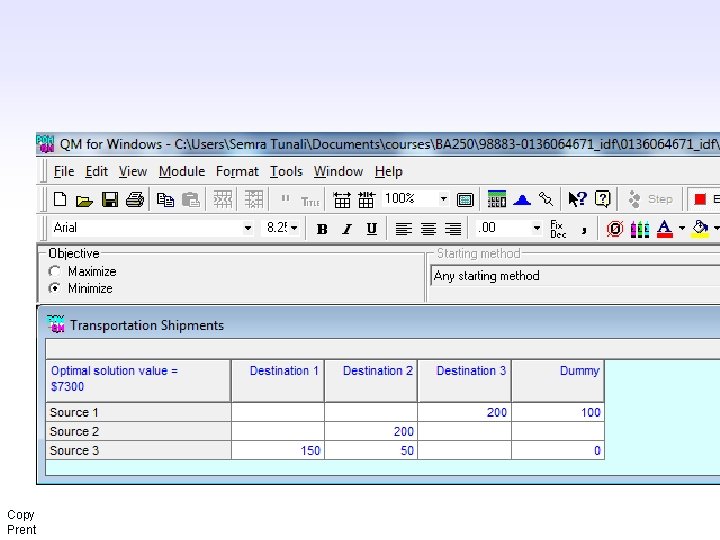
A Transportation Example n The manufacturer wants to know the number of television sets to ship from each warehouse to each store in order to minimize the total cost of transportation. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -24

A Transportation Example Model Summary (2 of 4) Minimize Z = $16 x 1 A + 18 x 1 B + 11 x 1 C + 14 x 2 A + 12 x 2 B + 13 x 2 C + 13 x 3 A + 15 x 3 B + 17 x 3 C subject to: x 1 A + x 1 B+ x 1 C 300 x 2 A+ x 2 B + x 2 C 200 Double-subscripted variable: xij : Number of products shipped from warehouse i to store j, for i=1, 2, 3 and j=A, B, C. x 3 A+ x 3 B + x 3 C 200 x 1 A + x 2 A + x 3 A = 150 x 1 B + x 2 B + x 3 B = 250 x 1 C + x 2 C + x 3 C = 200 All xij 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -25

Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -26

Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -27

Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -28

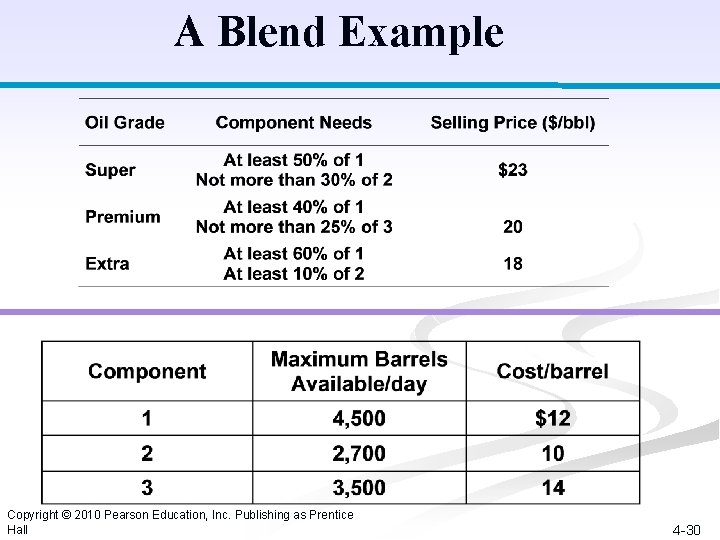
A Blend Example n. A petroleum company produces three grades of motor oil: super, premium, and extra from three components. n Company wants to produce at least 3, 000 barrels of each grade of motor oil per day. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -29

A Blend Example Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -30

A Blend Example Problem Statement ■ Determine the optimal mix of the three components in each grade of motor oil that will maximize daily profit. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -31

A Blend Example Decision variables: n The quantity of each of the three components used in each grade of gasoline (9 decision variables) n xij = barrels of component i used in motor oil grade j per day, where i = 1, 2, 3 and j = s (super), p (premium), and e (extra). n Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -32

A Blend Example We have 3 groups of constraints to model: - Company wants to produce at least 3, 000 barrels of each grade of motor oil (3 constraints for production level) - Barrels of components to use per day can not exceed the given levels (3 constraints for input) - Amount of components used in each grade of motor oil should comply with 4 -33 n Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall

A Blend Example Model Summary (3 of 6) Maximize Z = 11 x 1 s + 13 x 2 s + 9 x 3 s + 8 x 1 p + 10 x 2 p + 6 x 3 p + 6 x 1 e + 8 x 2 e + 4 x 3 e subject to: x 1 s + x 1 p + x 1 e 4, 500 bbl. x 2 s + x 2 p + x 2 e 2, 700 bbl. x 3 s + x 3 p + x 3 e 3, 500 bbl. 0. 50 x 1 s - 0. 50 x 2 s - 0. 50 x 3 s 0 0. 70 x 2 s - 0. 30 x 1 s - 0. 30 x 3 s 0 0. 60 x 1 p - 0. 40 x 2 p - 0. 40 x 3 p 0 0. 75 x 3 p - 0. 25 x 1 p - 0. 25 x 2 p 0 0. 40 x 1 e- 0. 60 x 2 e - 0. 60 x 3 e 0 0. 90 x 2 e - 0. 10 x 1 e - 0. 10 x 3 e 0 x 1 s + x 2 s + x 3 s 3, 000 bbl. x 1 p+ x 2 p + x 3 p 3, 000 bbl. all xij 0 x 1 e+ x 2 e + x 3 e 3, 000 bbl. Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -34

Solution for Blend Example n n n n X 1 s = 1500 barrels X 2 s = 600 barrels X 3 s = 900 barrels X 1 p = 1200 barrels X 2 p = 1800 barrels X 1 e = 1800 barrels X 2 e = 1300 barrels X 3 e = 900 barrels Z = $76800 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -35

A Multi-Period Scheduling Example PM Computer Services assembles its own brand of personal computers from component parts it purchases overseas and domestically. n PM sells most of its computers locally to different departments at State University as well as to individuals and businesses in the n Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -36

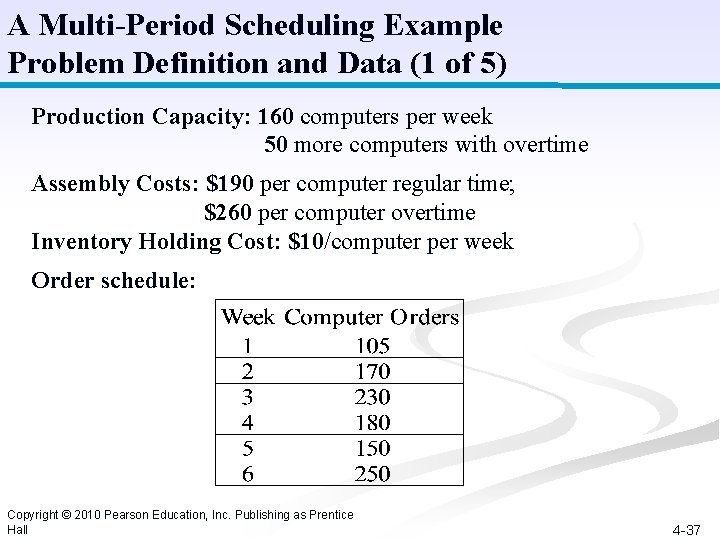
A Multi-Period Scheduling Example Problem Definition and Data (1 of 5) Production Capacity: 160 computers per week 50 more computers with overtime Assembly Costs: $190 per computer regular time; $260 per computer overtime Inventory Holding Cost: $10/computer per week Order schedule: Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -37

A Multi-Period Scheduling Example PM Computers wants to determine a schedule that will indicate how much regular and overtime production it will need each week to meet its orders at minimum cost. n Note that the company starts production with no inventory on hand wants no inventory left over at the end of the 6 -week n Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -38

A Multi-Period Scheduling Example Decision Variables (2 of 5) Decision Variables: rj = regular production of computers in week j (j = 1, 2, …, 6) oj = overtime production of computers in week j (j = 1, 2, …, 6) j ij = extra computers carried over as inventory in week (j = 1, 2, …, 5) Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -39

A Multi-Period Scheduling Example Model Summary (3 of 5) Model summary: Minimize Z = $190(r 1 + r 2 + r 3 + r 4 + r 5 + r 6) + $260(o 1+o 2 +o 3 +o 4+o 5+o 6) + 10(i 1 + i 2 + i 3 + i 4 + i 5) subject to: rj 160 computers in week j (j = 1, 2, 3, 4, 5, 6) oj 50 computers in week j (j = 1, 2, 3, 4, 5, 6) r 1 + o 1 - i 1 = 105 week 1 r 2 + o 2 + i 1 - i 2 = 170 week 2 r 3 + o 3 + i 2 - i 3 = 230 week 3 r 4 + o 4 + i 3 - i 4 = 180 week 4 r 5 + o 5 + i 4 - i 5 = 150 week 5 r 6 + o 6 + i 5 = 250 week 6 rj, oj, ij 0 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -40

Solution for Multi-Period Scheduling Example n n n n r 1 = 160 computers produced in regular time in week 1 r 2 = 160 computers produced in regular time in week 2 r 3 = 160 computers produced in regular time in week 3 r 4 = 160 computers produced in regular time in week 4 r 5= 160 computers produced in regular time in week 5 r 6 = 160 computers produced in regular time in week 6 o 3 = 25 computer produced with overtime in week 3 o 4 = 20 computer produced with overtime in week 4 o 5 = 30 computer produced with overtime in week 5 o 6 = 50 computer produced with overtime in week 6 i 1 = 55 computers carried over in inventory in week 1 i 2 = 45 computers carried over in inventory in week 2 i 5 = 40 computers carried over in inventory in week 5 Copyright © 2010 Pearson Education, Inc. Publishing as Prentice Hall 4 -41