LINEAR PROGRAMMING MEANING it is a mathematical technique














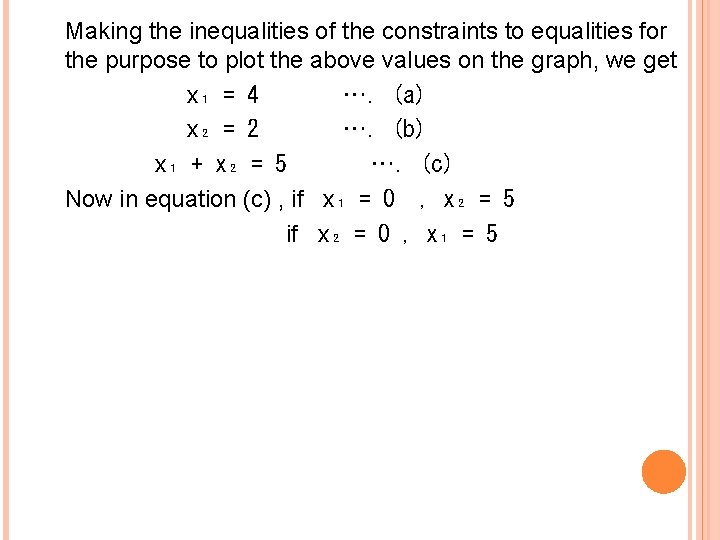



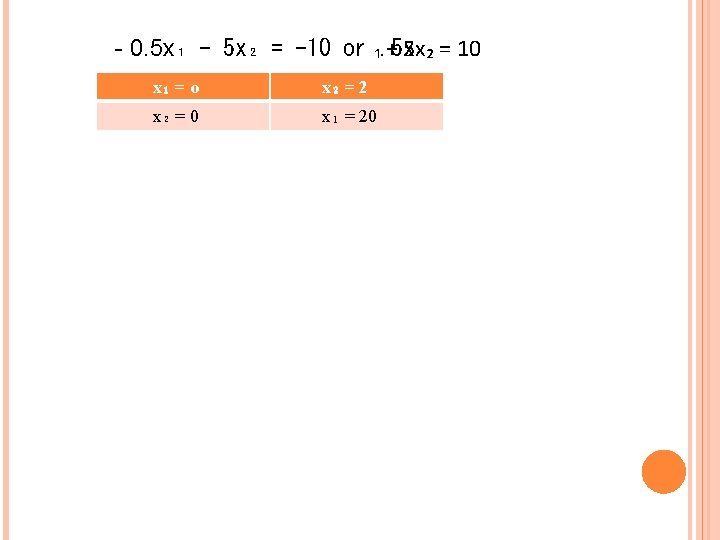



- Slides: 36

LINEAR PROGRAMMING MEANING: it is a mathematical technique for finding the best use of an organization’s resources. It is designed to help managers in planning and decision making. It has demonstrated its value in different areas such as production, finance, marketing, research and personnel assignments. .

TERMINOLOGY AND REQUIREMENTS OF LPP OBJECTIVE FUNCTION PRESENCE OF CONSTRAINTS AND RESTRICTIONS ALTERNATIVE COURSE OF ACTION NEGATIVITY CONSTRAINTS LINEARITY FINITE NUMBER OF VARIABLES BASIC VARIABLES SLACK VARIABLES SURPLUS VARIABLES ARTIFICIAL VARIABLES OPTIMUM SOLUTION

APPLICATIONS OF LPP PRODUCT MIX DIET PROBLEM THE PORTFOLIO SELECTION PROBLEM MEDIA SELECTION BLENDING PROBLEM TRANSPORTATION PROBLEM TRAVELLING SALESMAN PROBLEM

PRODUCT MIX PROBLEM Q 1. A firm is engaged in producing two products P 1 and P 2. Each unit of product P 1 requires 2 kg of raw material and 4 labor hours for processing, where each unit of product P 2 requires 5 kg of raw materials and 3 labor hours of the same type. Every week the firm has the availability of 50 kg of raw material and 60 labor hours. One unit of product P 1 sold earn profit rs 20 and one unit of product P 2 sold gives rs 30 as profit.

SOLUTION : MAXIMISE Z = 20 x 1 + 30 x 2 SUBJECT TO 2 X 1 + 5 X 2 ≤ 50 4 x 1 + 3 x 2 ≤ 60 Where x 1, x 2 ≥ 0

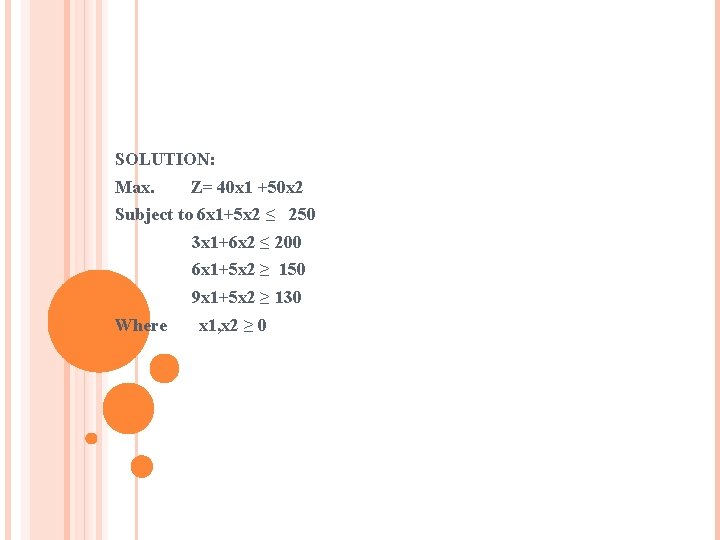
BLENDING PROBLEM Q 2. THE MANAGER OF AN OIL REFINERY MUST DECIDE ON THE OPTIMAL MIX OF 2 POSSIBLE BLENDING PROCESS OF WHICH THE INPUTS AND OUTPUTS PER PRODUCTION RUN ARE AS FOLLOWS: PROCESS INPUT CRUDE A INPUT CRUDE B OUTPUT GASOLINE A GASOLINE B 1 2 6 5 3 6 6 5 9 5 The maximum availability crude A & B are 250 units and 200 units. The market requirement shows that at least 150 units of gasoline X and 130 units of gasoline Y must be produce. the profit per production run from process 1&2 are Rs. 40 & Rs. 50. Formulate the problems for maximize profit.

SOLUTION: Max. Z= 40 x 1 +50 x 2 Subject to 6 x 1+5 x 2 ≤ 250 3 x 1+6 x 2 ≤ 200 6 x 1+5 x 2 ≥ 150 9 x 1+5 x 2 ≥ 130 Where x 1, x 2 ≥ 0

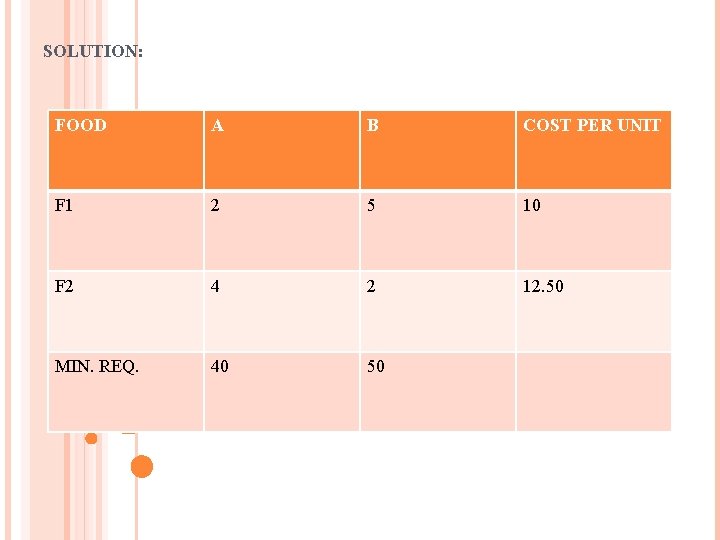
DIET PROBLEMS Q 3. Vitamins A&B are found in two different food F 1 & F 2. one unit of food F 1 contains 2 units vitamin A and 5 units vitamin B. One unit of F 2 contains 4 units of vitamin A and 2 units of vitamin B. One unit of F 1&F 2 cost Rs. 10 & Rs. 12. 5. the minimum daily requirements of vitamin A&B is 40&50 units. Find out the optimal minimum of F 1& F 2 and minimum cost which meets the daily minimum requirements of vitamin A & B.

SOLUTION: FOOD A B COST PER UNIT F 1 2 5 10 F 2 4 2 12. 50 MIN. REQ. 40 50

Min Z= 10 X 1+12. 5 X 2 SUBJECT TO 2 X 1+4 X 2 ≥ 40 5 X 1+2 X 2 ≥ 50 WHERE X 1, X 2 ≥ 0

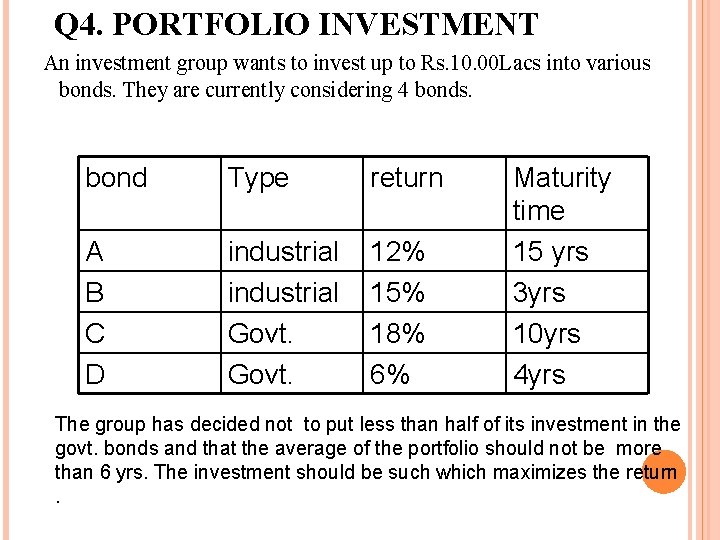
Q 4. PORTFOLIO INVESTMENT An investment group wants to invest up to Rs. 10. 00 Lacs into various bonds. They are currently considering 4 bonds. bond Type return A B C D industrial Govt. 12% 15% 18% 6% Maturity time 15 yrs 3 yrs 10 yrs 4 yrs The group has decided not to put less than half of its investment in the govt. bonds and that the average of the portfolio should not be more than 6 yrs. The investment should be such which maximizes the return.

MAX Z=. 12 X 1+. 15 X 2+. 18 X 3+. 6 X 4 SUBJECT TO X 1+X 2+X 3+X 4 ≤ 1000000 X 3+X 4 ≥ 500000 9 X 1 -3 X 2+4 X 3 -2 X 4 ≤ 0 WHERE X 1, X 2, X 3, X 4 ≥ 0

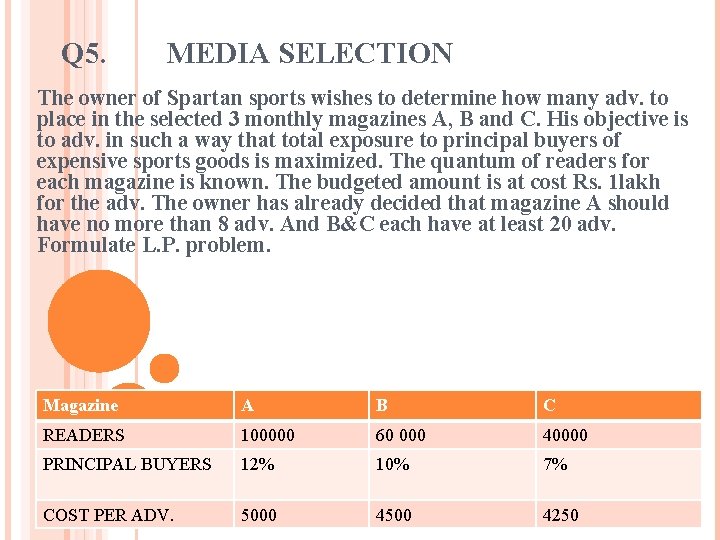
Q 5. MEDIA SELECTION The owner of Spartan sports wishes to determine how many adv. to place in the selected 3 monthly magazines A, B and C. His objective is to adv. in such a way that total exposure to principal buyers of expensive sports goods is maximized. The quantum of readers for each magazine is known. The budgeted amount is at cost Rs. 1 lakh for the adv. The owner has already decided that magazine A should have no more than 8 adv. And B&C each have at least 20 adv. Formulate L. P. problem. Magazine A B C READERS 100000 60 000 40000 PRINCIPAL BUYERS 12% 10% 7% COST PER ADV. 5000 4500 4250

MAXIMISE Z=12000 X 1+6000 X 2+2800 X 3 SUBJECT TO 5000 X 1+4500 X 2+4250 X 3 ≤ 100000 X 1 ≤ 8 X 2 ≥ 20 X 3 ≥ 20 WHERE X 1, X 2, x 3 ≥ 0

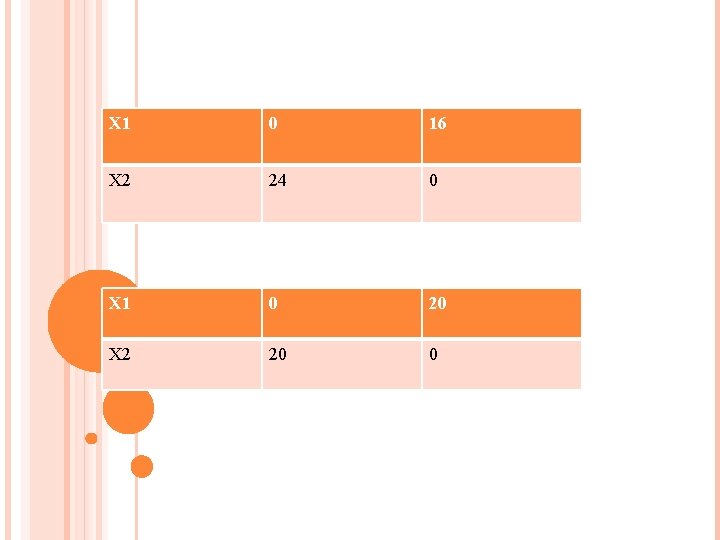
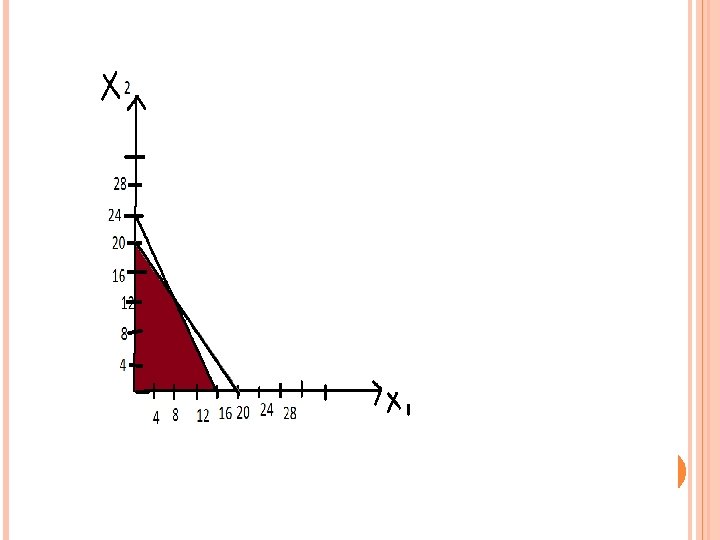
Q 7. A dealer wishes to purchase a number of fans and sewing machine. He has only Rs. 5760/- to invest and has space for almost 20 items. A fan cost him Rs. 360/- and a sewing machine Rs. 240/- his expectation is that he can sell a fan at profit of Rs. 22/- and a sewing machine @Rs. 18/-. how should he invest his money in order to maximize his profit.

SOLUTION MAX. Z=22 x 1+18 x 2 Subject to 360 x 1+240 x 2 ≤ 5760 or 3 x 1+2 x 2 ≤ 48 x 1 +x 2 ≤ 20 Where x 1, x 2 ≥ 0

X 1 0 16 X 2 24 0 X 1 0 20 X 2 20 0


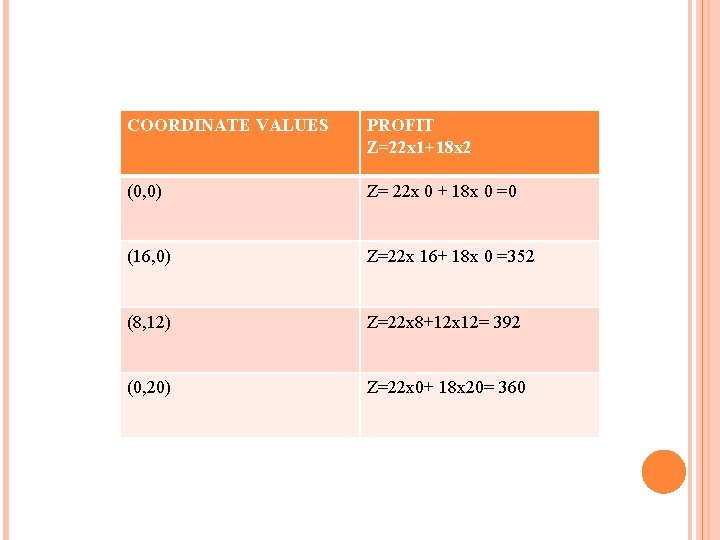
COORDINATE VALUES PROFIT Z=22 x 1+18 x 2 (0, 0) Z= 22 x 0 + 18 x 0 =0 (16, 0) Z=22 x 16+ 18 x 0 =352 (8, 12) Z=22 x 8+12 x 12= 392 (0, 20) Z=22 x 0+ 18 x 20= 360

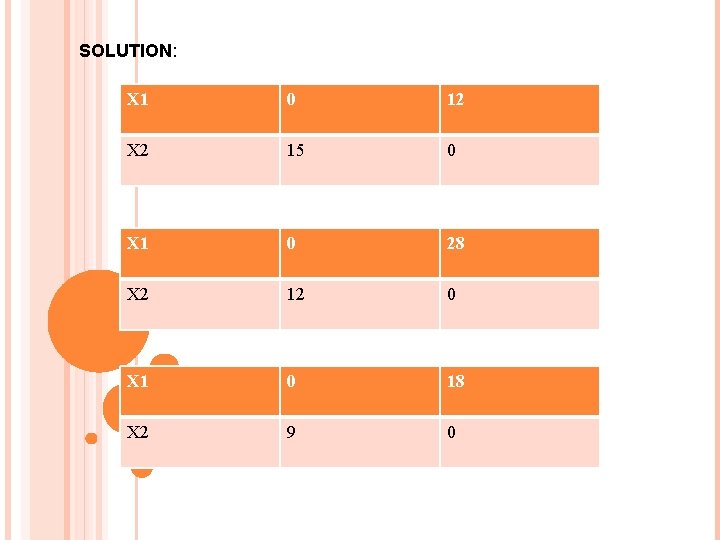
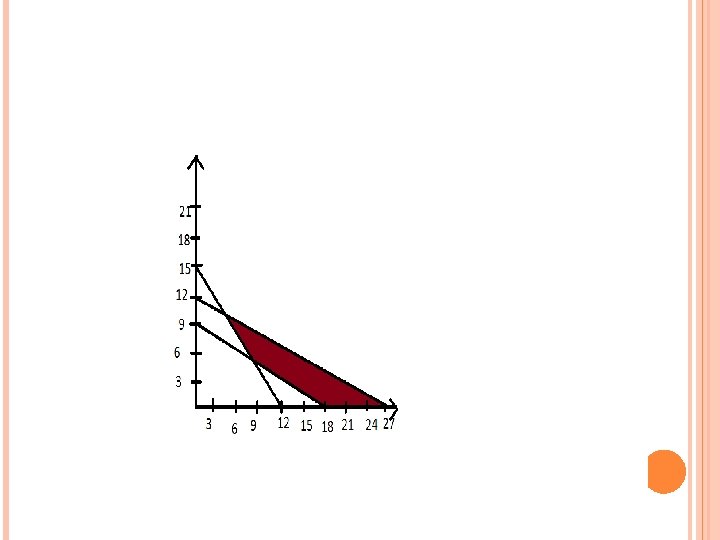
Q 6. SOLVE GRAPHICALLY Min. Z=6 X 1+14 x 2 Subject to 5 x 1+4 x 2 ≥ 60 3 x 1+7 x 2≤ 84 x 1+2 x 2 ≥ 18 Where x 1, x 2 ≥ 0

SOLUTION: X 1 0 12 X 2 15 0 X 1 0 28 X 2 12 0 X 1 0 18 X 2 9 0

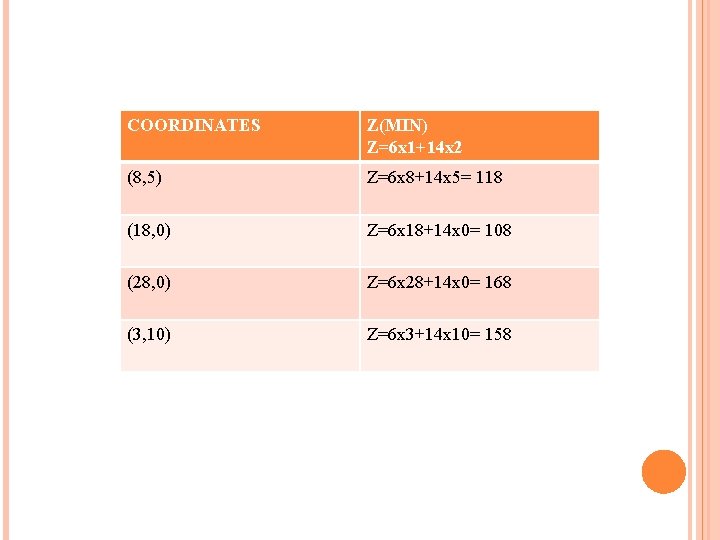
COORDINATES Z(MIN) Z=6 x 1+14 x 2 (8, 5) Z=6 x 8+14 x 5= 118 (18, 0) Z=6 x 18+14 x 0= 108 (28, 0) Z=6 x 28+14 x 0= 168 (3, 10) Z=6 x 3+14 x 10= 158


Ques. The standard weight of a special purpose brick is 5 kg and it contains two basic ingredients B 1 and B 2 costs Rs. 8 per kg. Strength considerations dictate that the brick contains not more than 4 kg of B 1 minimum of 2 kg of B 2. Since the demand for the product is likely to be related to the price of the brick, find out graphically minimum cost of the brick satisfying the above conditions. Solution The mathematical formulation of the given LPP is: Minimize Z = 5 x₁ + 8 x₂ (Cost function) Subject to x₁ ˂ 4 x₂ ˃ 2 x₁ + x₂ = 5 Where x₁ , x₂˃ 0 (Non negativity)
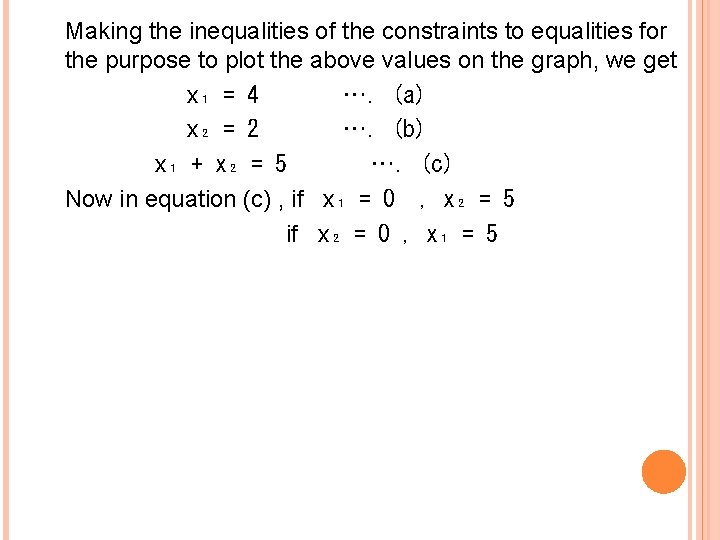
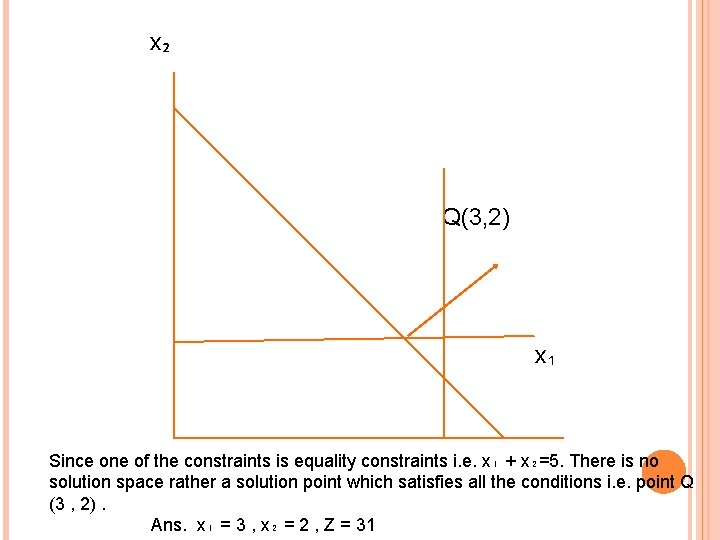
Making the inequalities of the constraints to equalities for the purpose to plot the above values on the graph, we get x₁ = 4 …. (a) x₂ = 2 …. (b) x₁ + x₂ = 5 …. (c) Now in equation (c) , if x₁ = 0 , x₂ = 5 if x₂ = 0 , x₁ = 5

x₂ Q(3, 2) x₁ Since one of the constraints is equality constraints i. e. x₁ + x₂=5. There is no solution space rather a solution point which satisfies all the conditions i. e. point Q (3 , 2). Ans. x₁ = 3 , x₂ = 2 , Z = 31

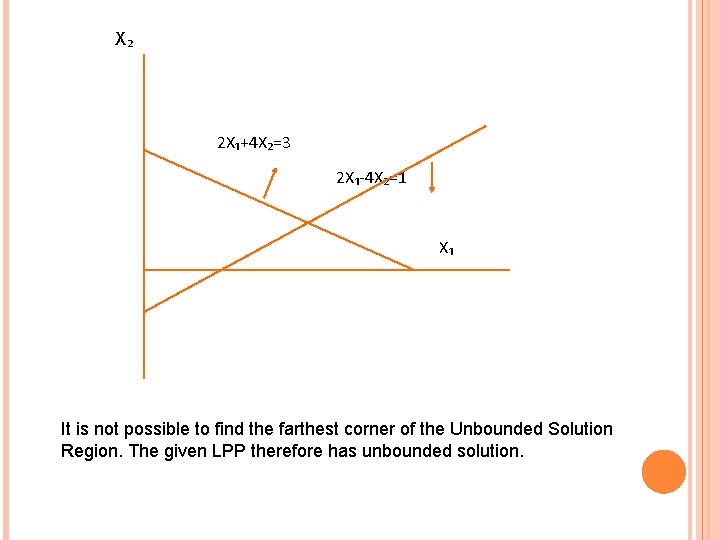
UNBOUNDED PROBLEM Ques. Solve the LPP by Graphic Method: Maximize Z = 5 x₁ + 4 x₂ Subject to 2 x₁ - 4 x₂˂ 1 2 x₁ + 4 x₂˃ 3 x₁ , x₂> 0 Solution Making the inequalities into equalities: 2 x₁ - 4 x₂ = 1 x₁ = 0 x₂ = - 1/4 x₂ = 0 x₁ = 1/2


X₂ 2 X₁+4 X₂=3 2 X₁-4 X₂=1 X₁ It is not possible to find the farthest corner of the Unbounded Solution Region. The given LPP therefore has unbounded solution.

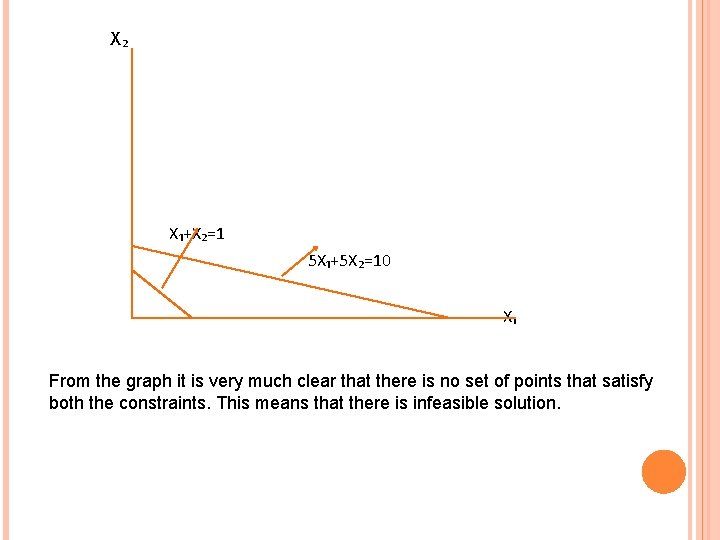
INFEASIBLE PROBLEM Ques. Solve graphically Find the maximum value of Z = -5 x₂ Subject to x₁ + x₂< 1 -0. 5 x₁ - 5 x₂< -10 x₁ , x₂> 0 Solution Making inequalities of the constraints to equalities: x₁ + x₂ = 1 x₁ = 0 x₂ = 1 x₂ = 0 x₁ = 1
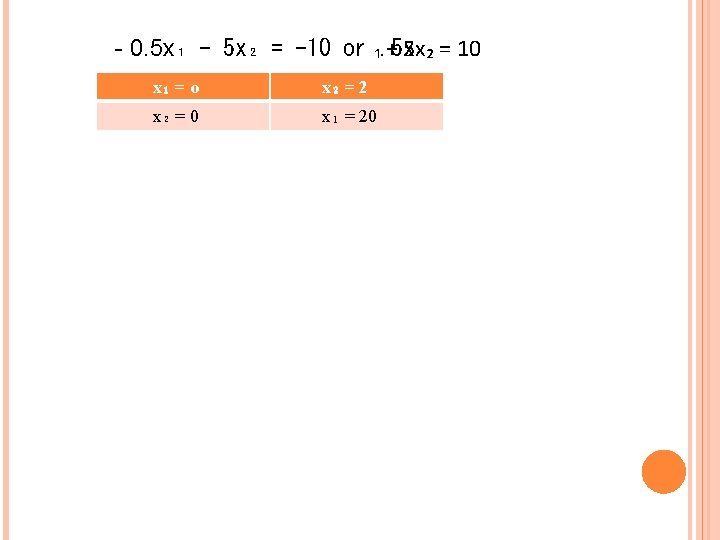

X₂ X₁+X₂=1 5 X₁+5 X₂=10 X₁ From the graph it is very much clear that there is no set of points that satisfy both the constraints. This means that there is infeasible solution.

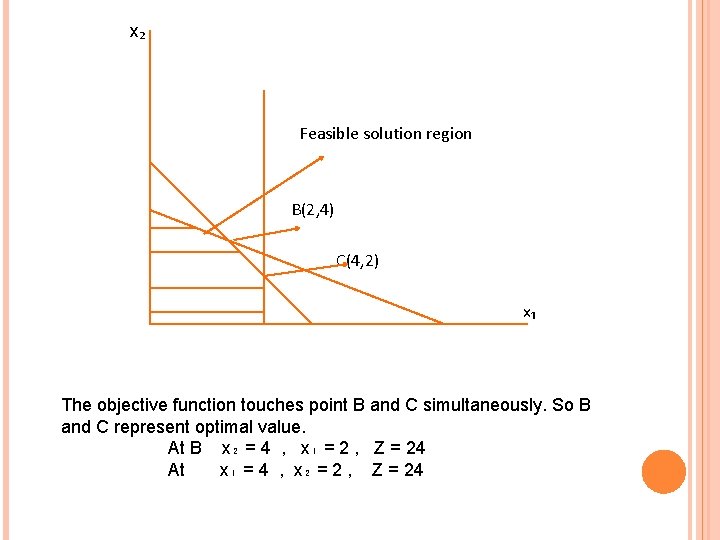
MULTIPLE OPTIMAL SOLUTIONS Ques. Maximize Subject to. Z = 4 x₁ + 4 x₂ x₁ + 2 x₂< 10 6 x₁ + 6 x₂< 36 x₁ < 4 x₁ , x₂> 0 Solution Making inequalities to equalities x₁ + 2 x₂ = 10 x₂ = 0 x₁ = 10 x₁ = 0 x₂ = 5


x₂ Feasible solution region B(2, 4) C(4, 2) x₁ The objective function touches point B and C simultaneously. So B and C represent optimal value. At B x₂ = 4 , x₁ = 2 , Z = 24 At x₁ = 4 , x₂ = 2 , Z = 24

THANK YOU