Linear Programming Mathematical Technique for Solving Constrained Maximization







- Slides: 17

Linear Programming • Mathematical Technique for Solving Constrained Maximization and Minimization Problems • Assumes that the Objective Function is Linear • Assumes that All Constraints Are Linear Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

Applications of Linear Programming • • • Optimal Process Selection Optimal Product Mix Satisfying Minimum Product Requirements Long-Run Capacity Planning Least Cost Shipping Route (Transportation Problems) Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

Applications of Linear Programming • Airline Operations Planning • Output Planning with Resource and Process Capacity Constraints • Distribution of Advertising Budget • Routing of Long-Distance Phone Calls • Investment Portfolio Selection • Allocation of Personnel Among Activities Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

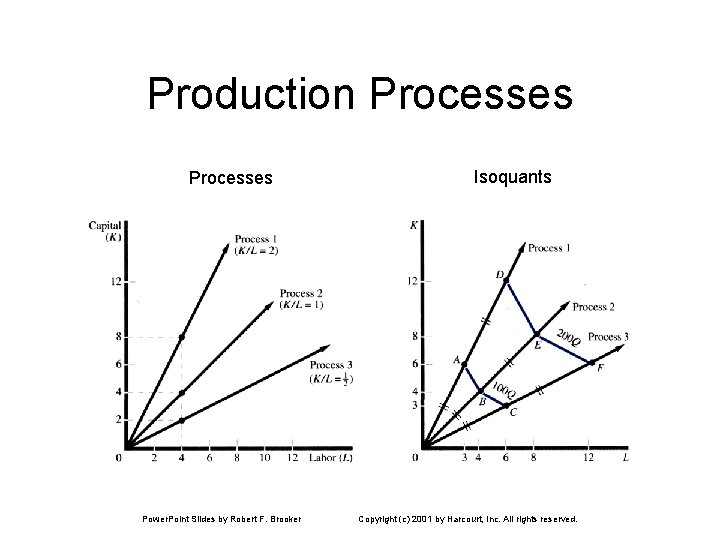
Production Processes Production processes are graphed as linear rays from the origin in input space. Production isoquants are line segments that join points of equal output on the production process rays. Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

Production Processes Power. Point Slides by Robert F. Brooker Isoquants Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

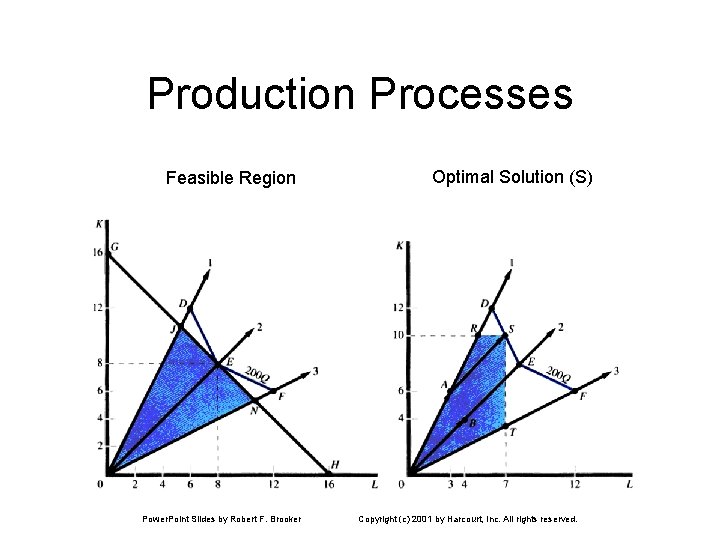
Production Processes Feasible Region Power. Point Slides by Robert F. Brooker Optimal Solution (S) Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

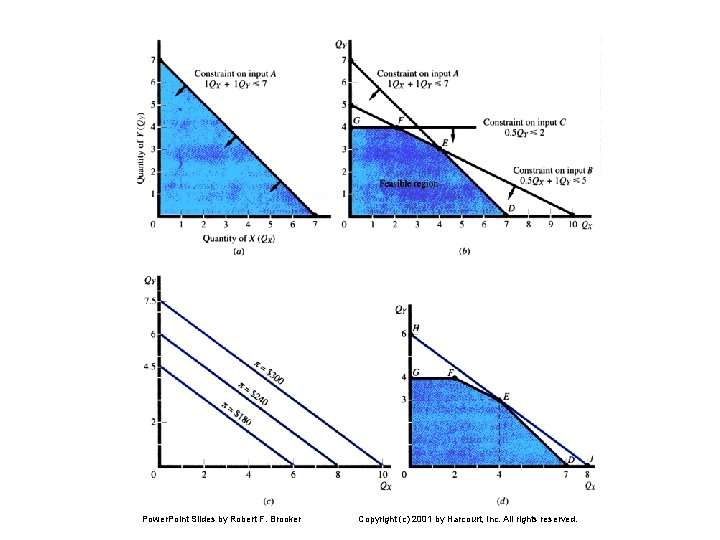
Formulating and Solving Linear Programming Problems • Express Objective Function as an Equation and Constraints as Inequalities • Graph the Inequality Constraints and Define the Feasible Region • Graph the Objective Function as a Series of Isoprofit or Isocost Lines • Identify the Optimal Solution Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

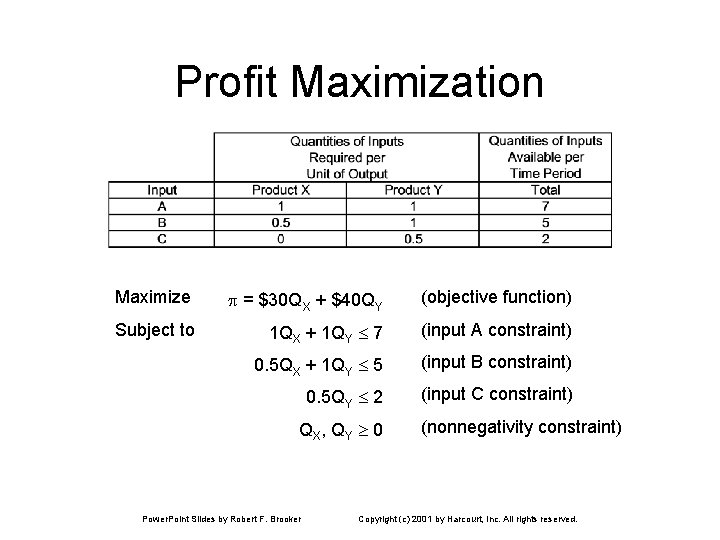
Profit Maximization Maximize = $30 QX + $40 QY (objective function) Subject to 1 QX + 1 QY 7 (input A constraint) 0. 5 QX + 1 QY 5 (input B constraint) 0. 5 QY 2 (input C constraint) QX, QY 0 Power. Point Slides by Robert F. Brooker (nonnegativity constraint) Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

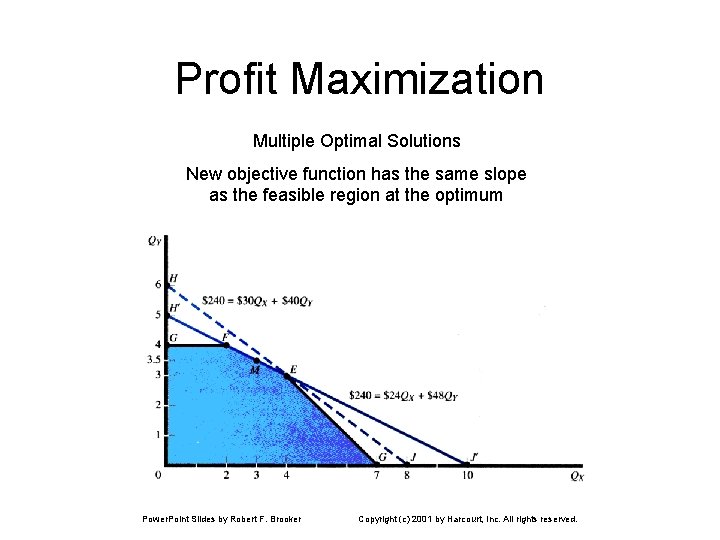
Profit Maximization Multiple Optimal Solutions New objective function has the same slope as the feasible region at the optimum Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

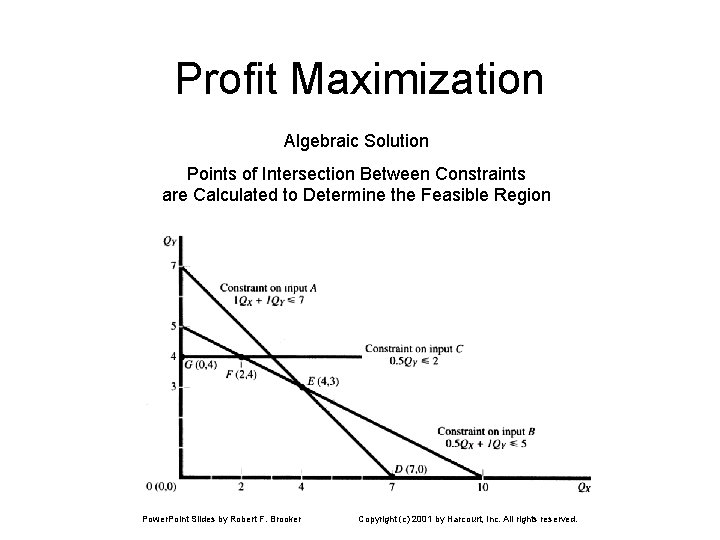
Profit Maximization Algebraic Solution Points of Intersection Between Constraints are Calculated to Determine the Feasible Region Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

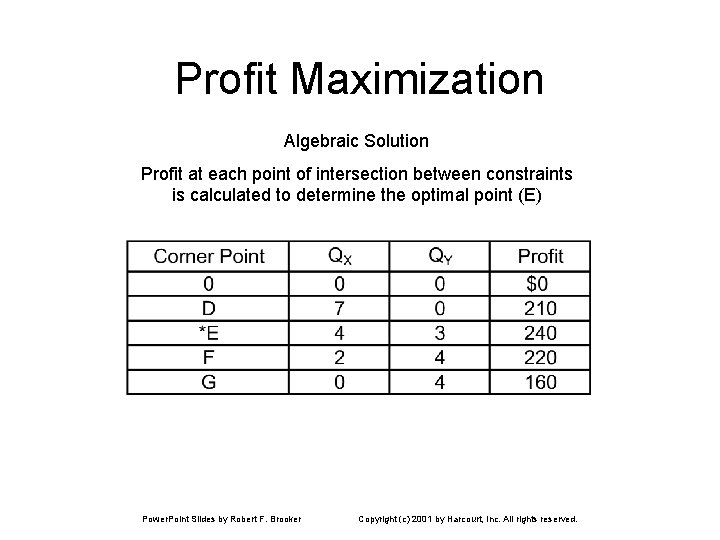
Profit Maximization Algebraic Solution Profit at each point of intersection between constraints is calculated to determine the optimal point (E) Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

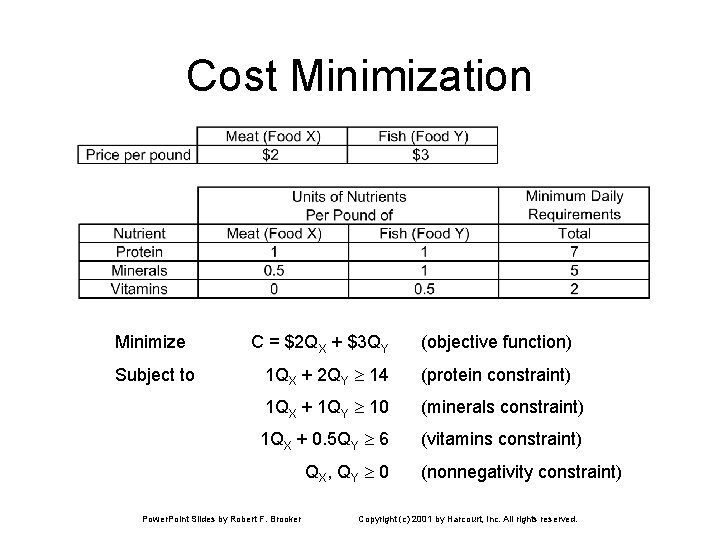
Cost Minimization Minimize Subject to C = $2 QX + $3 QY (objective function) 1 QX + 2 QY 14 (protein constraint) 1 QX + 1 QY 10 (minerals constraint) 1 QX + 0. 5 QY 6 (vitamins constraint) QX, QY 0 Power. Point Slides by Robert F. Brooker (nonnegativity constraint) Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

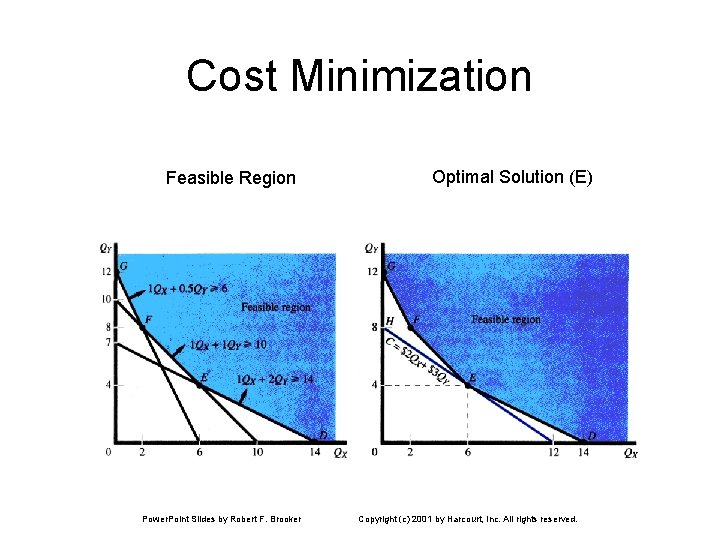
Cost Minimization Feasible Region Power. Point Slides by Robert F. Brooker Optimal Solution (E) Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

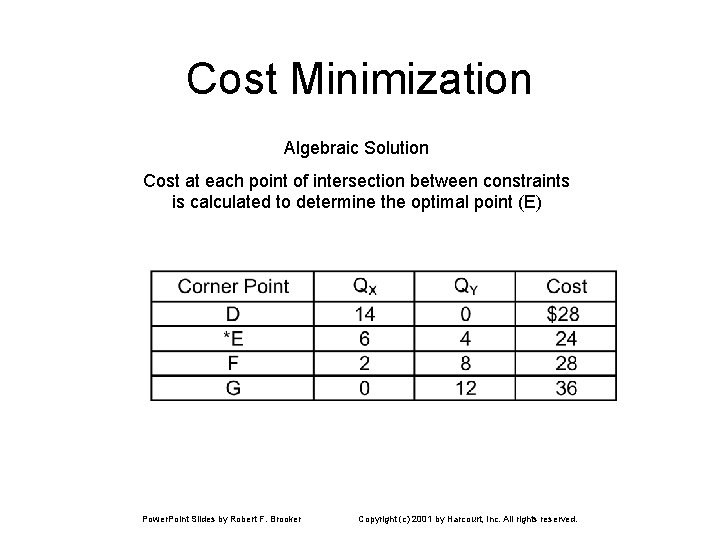
Cost Minimization Algebraic Solution Cost at each point of intersection between constraints is calculated to determine the optimal point (E) Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

Dual of the Profit Maximization Problem Maximize = $30 QX + $40 QY (objective function) Subject to 1 QX + 1 QY 7 (input A constraint) 0. 5 QX + 1 QY 5 (input B constraint) 0. 5 QY 2 (input C constraint) QX, QY 0 Minimize Subject to (nonnegativity constraint) C = 7 VA + 5 VB + 2 VC 1 VA + 0. 5 VB $30 1 VA + 1 VB + 0. 5 VC $40 VA, VB, VC 0 Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.

Dual of the Cost Minimization Problem Minimize Subject to C = $2 QX + $3 QY (objective function) 1 QX + 2 QY 14 (protein constraint) 1 QX + 1 QY 10 (minerals constraint) 1 QX + 0. 5 QY 6 (vitamins constraint) QX, QY 0 (nonnegativity constraint) Maximize = 14 VP + 10 VM + 6 VV Subject to 1 VP + 1 VM + 1 VV $30 2 VP + 1 VM + 0. 5 VV $40 VP, VM, VV 0 Power. Point Slides by Robert F. Brooker Copyright (c) 2001 by Harcourt, Inc. All rights reserved.