Linear Programming LP Vector Form Maximize cx Subject

Linear Programming (LP) • Vector Form Maximize: cx Subject to : Ax b c = (c 1, c 2, …, cn) x 1 b 1. x= b=. . . xn bn A = a 11 … a 1 n …… …… an 1 … amn • Summation Form Maximize: cixi Subject to: a 1 ixi b 1 a 2 ixi b 2. . amixi bm

Example LP n = 2; m = 4 x 1 + x 2 max x 1 0 (-1)x 1 + 0 x 2 0 0 x 1 + (-1)x 2 0 x 1 5 (-1)x 1 + 0 x 2 5 x 2 6 0 x 1 + 1 x 2 6 0 c = (1, 1) b= 0 5 -1 0 6 A = 0 -1 1 0 0 1 • Optimal solution is the unique point of intersection of the objective with the hyperplane feasible polytope. x 2 optimal solution x 1 = 5 ; x 2 = 6 objective: Feasible x 1 + x 2 = 11 solution region x 1

Integer Linear Programming (ILP) • Vector Form Maximize: cx Subject to : Ax b and x {0, 1} c = (c 1, c 2, …, cn) x= x 1. . xn A = b= a 11 … a 1 n …… …… an 1 … amn b 1. . bn • Summation Form Maximize: cixi Subject to: a 1 ixi b 1 a 2 ixi b 2. . amixi bm and x {0, 1}

ILP for MIS • Maximum Independent Set (MIS) - Find the maximum subset of nodes in graph G = (V, E) which are pairwise non-adjacent • ILP - For any v V make a variable xv {0, 1} xv = 0 v MIS which means 0 is not chosen xv = 1 v MIS which means 1 is chosen - Maximize v V xv Subject to: e = (u, v) V, xu + xv 1

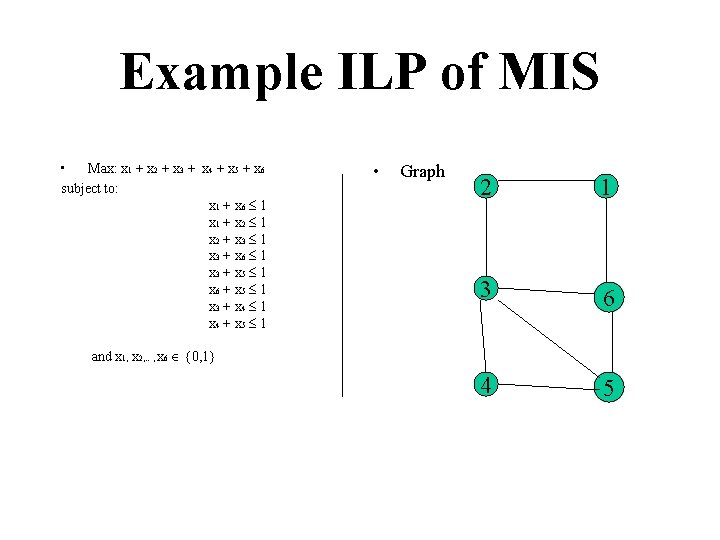
Example ILP of MIS • Max: x 1 + x 2 + x 3 + x 4 + x 5 + x 6 subject to: x 1 + x 6 1 x 1 + x 2 1 x 2 + x 3 1 x 3 + x 6 1 x 3 + x 5 1 x 6 + x 5 1 x 3 + x 4 1 x 4 + x 5 1 • Graph 2 1 3 6 4 5 and x 1, x 2, …, x 6 {0, 1}

ILP for Max. Clique • Max. Clique - Given G = (V, E) - Find X V x, x’ X (x, x’) E |X| max • ILP - xi max Subject to: xi + xj 1 (i, j) E

ILP for Matching • Matching • ILP - for any e E xe {0, 1} + 0 is not in matching + 1 is in matching - e E xe max - Subject to: e incident to V xe 1 v V - Given G = (V, E) - Find X E e, e’ X e and e’ don’t share endpoint. |X| max xe 1 + xe 2 + xe 3 1 e 2 e 1 v only one edge from e 3 matching can be incident to v

LP relaxation (LPR) vs. ILP LP relaxation (LPR) for MAX independent set problem (MISP) gives larger value than the maximum size of independent set. • MISP xi max, i V xi + xj 1, for each edge (xi, xj) E xi {0, 1} • LPR xi max, i V xi + xj 1, for each edge (xi, xj) E 0 xi 1

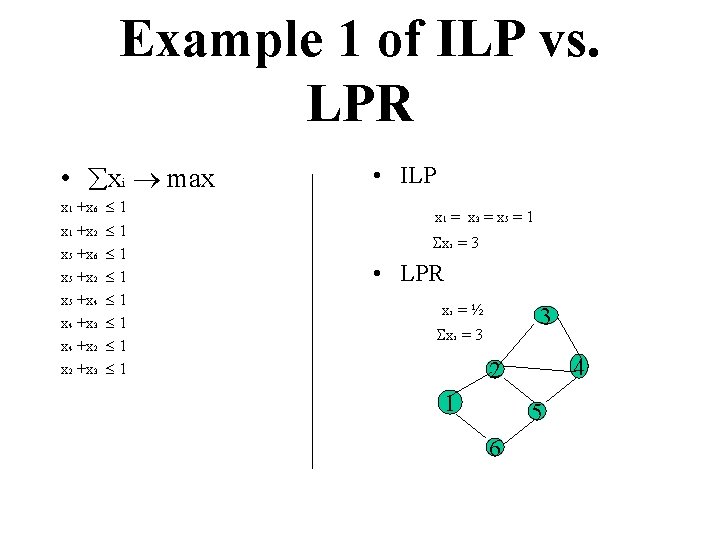
Example 1 of ILP vs. LPR • xi max x 1 +x 6 x 1 +x 2 x 5 +x 6 x 5 +x 2 x 5 +x 4 +x 3 x 4 +x 2 +x 3 1 1 1 1 • ILP x 1 = x 3 = x 5 = 1 xi = 3 • LPR xi = ½ 3 xi = 3 4 2 1 5 6

MISP Integrality Gap • x 1 +x 2 + x 3 max x 1 +x 2 1 x 1 +x 3 1 x 2 +x 3 1 0 x 1 1 0 x 2 1 0 x 3 1 LPR ( ) 3/2 Implies LPR ( ) = 3/2 So x 1 = x 2 = x 3 = ½ LPR ( ) 3/2 ILP ( ) = 1 Integrality Gap (IG) = LPR / ILP = 3/2 • What is the integrality gap for (MISP) For a complete graph ILP (Kn) = 1 LPR (Kn) = n/2 Integrality Gap (IG) = LPR / ILP Integrality gap may be as large as n/2 2 1 3

LPR vs. ILP LP relaxation (LPR) for Minimum Vertex Cover problem (MVCP) gives smaller value than the minimum size of vertex cover • MVCP xi min, i V xi + xj 1, for each e= (xi, xj) E xi {0, 1} • LPR xi min , i V xi + xj 1, for each e= (xi, xj) E 0 xi 1

MVCP Integrality Gap • x 1 +x 2 + x 3 min x 1 +x 2 1 x 1 +x 3 1 x 2 +x 3 1 0 x 1 1 0 x 2 1 0 x 3 1 LPR ( ) 3/2 2 • What is the integrality gap for (MVCP) For a complete graph 1 3 Implies LPR ( ) = 3/2 So x 1 = x 2 = x 3 = ½ LPR ( ) 3/2 ILP ( ) = 2 Integrality Gap (IG) = ILP / LPR = 4/3 ILP (Kn) = n - 1 LPR (Kn) = n/2 Integrality Gap (IG) = ILP / LPR Integrality gap may be as large as 2 – (2 / n) For more information: http: //wwwunix. mcs. anl. gov/otc/Guide/faq/lin ear-programming-faq. html