Linear Programming LP constrains objective function Generally maximizing

선형계획법(Linear Programming: LP) · 자원에 제약(constrains)이 있는 문제에 사용. · 모델은 목적함수(objective function)를 가짐 – Generally maximizing profit or minimizing costs subject to resource-based, or other, constraints. · 목적함수와 제약식은 모두 선형(Linearity)임 · Variables must be divisible (i. e. , permit fractional values if need be) and nonnegative. 1

LP의 목적함수(Objective Function) Maximize (or Minimize) Z = C 1 X 1 + C 2 X 2 +. . . + Cn. Xn · Cj is a constant that describes the rate of contribution to costs or profit of units being produced (Xj). · Z is the total cost or profit from the given number of units being produced. 2

LP의 제약식(Constraints) A 11 X 1 + A 12 X 2 +. . . + A 1 n. Xn B 1 A 21 X 1 + A 22 X 2 +. . . + A 2 n. Xn B 2 : : AM 1 X 1 + AM 2 X 2 +. . . + AMn. Xn=BM · · · Aij are resource requirements for each of the related (Xj) decision variables. Bi are the available resource requirements. Note that the direction of the inequalities can be all or a combination of , , or = linear mathematical expressions. 3

Non-Negativity Requirement X 1, X 2, …, Xn 0 · · All linear programming model formulations require their decision variables to be nonnegative. While these non-negativity requirements take the form of a constraint, they are considered a mathematical requirement to complete the formulation of an LP model. 4

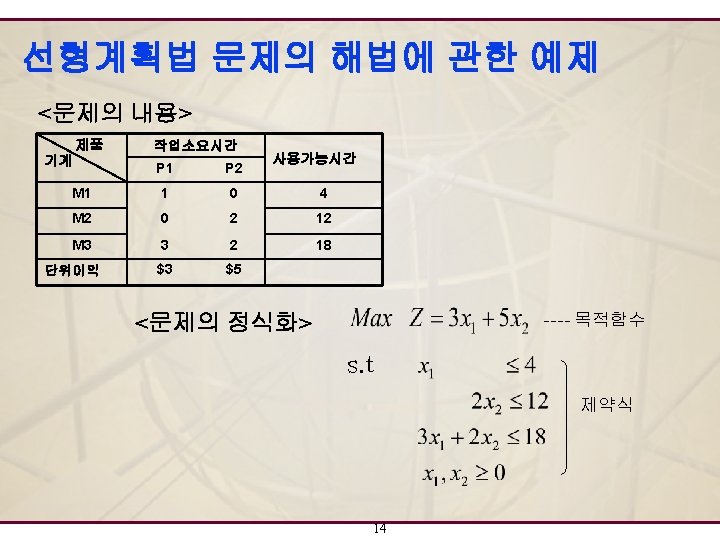
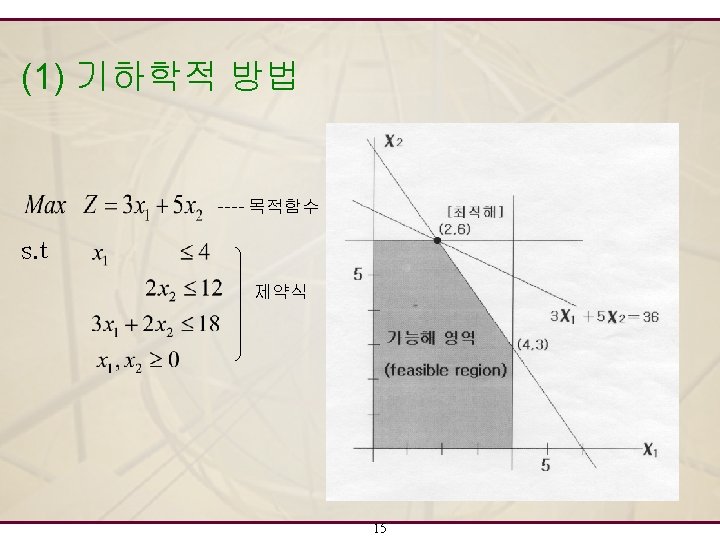
최대화 문제(Maximization Problem)의 예 (문제의 내용) Company must determine the mix of its products to be produced next year. The company produces two product lines, the A and the B. The average profit is $400 for each A and $800 for each B. Fabrication and assembly are limited resources. There is a maximum of 5, 000 hours of fabrication capacity available per month (Each A requires 3 hours and each B requires 5 hours). There is a maximum of 3, 000 hours of assembly capacity available per month (Each A requires 1 hour and each B requires 4 hours). (질문): How many of each product should be produced each month in order to maximize profit? 이 문제를 정식화해 봅시다…. 5

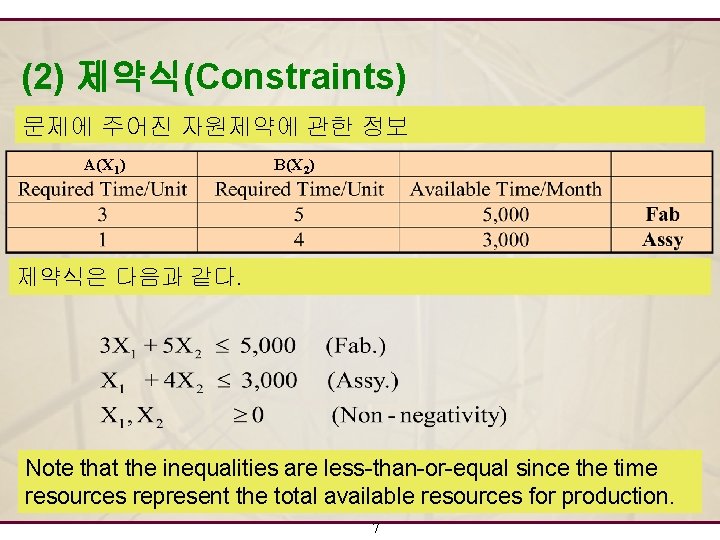
(2) 제약식(Constraints) 문제에 주어진 자원제약에 관한 정보 A(X 1) B(X 2) 제약식은 다음과 같다. Note that the inequalities are less-than-or-equal since the time resources represent the total available resources for production. 7

(3) 해답(Solution) 생산량: A = 715 개, B = 571 개 (per month) 전체 이윤 = $742, 800. 8

최소화 문제(Minimization Problem)의 예 (문제 내용) ABC Company is developing a plan for buying scrap metal for its operations. ABC receives scrap metal from two sources, H Industries and G Scrap in daily shipments using large trucks. Each truckload of scrap from H yields 1. 5 tons of zinc and 1 ton of lead at a cost of $15, 000. Each truckload of scrap from G yields 1 ton of zinc and 3 tons of lead at a cost of $18, 000. ABC requires at least 6 tons of zinc and at least 10 tons of lead per day. (질문): How many truckloads of scrap should be purchased per day from each source in order to minimize scrap metal cost? 이 문제를 정식화해 보면…. 9

(1) 목적함수 H truckloads 와 G truckloads 를 2개의 의사결정변수를 X 1 과 X 2 라 정의하면, 목적함수는 다음과 같이 최소화 문제이다. Minimize Z = 15, 000 X 1 + 18, 000 X 2 단, Z= X 1 = X 2 = daily scrap cost truckloads from H truckloads from G Hasbeen Gentro 10
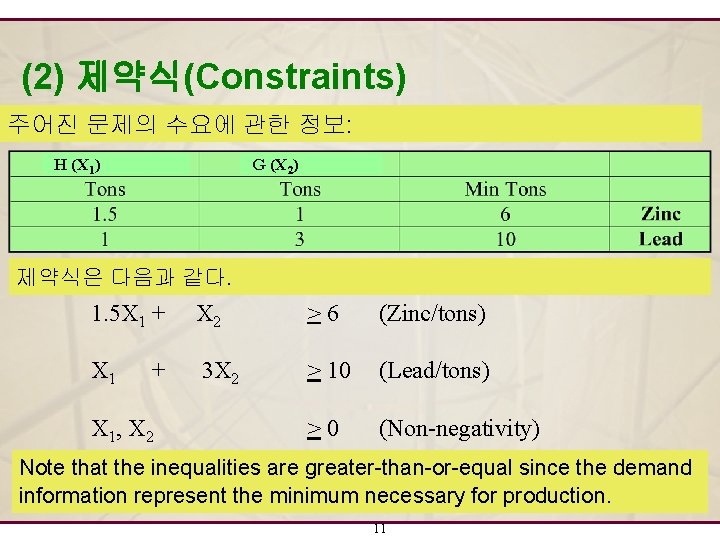
(2) 제약식(Constraints) 주어진 문제의 수요에 관한 정보: H (X 1) G (X 2) 제약식은 다음과 같다. 1. 5 X 1 + X 2 >6 (Zinc/tons) X 1 3 X 2 > 10 (Lead/tons) >0 (Non-negativity) + X 1, X 2 Note that the inequalities are greater-than-or-equal since the demand information represent the minimum necessary for production. 11

(3) 해답 Order 2. 29 truckloads from H and 2. 57 truckloads from G for daily delivery. The daily cost will be $80, 610. 12


(2) Simplex 방법 16
![[Simplex 표] 17 [Simplex 표] 17](http://slidetodoc.com/presentation_image_h/a4efda09105f194b06c9276c716fe10b/image-17.jpg)
[Simplex 표] 17

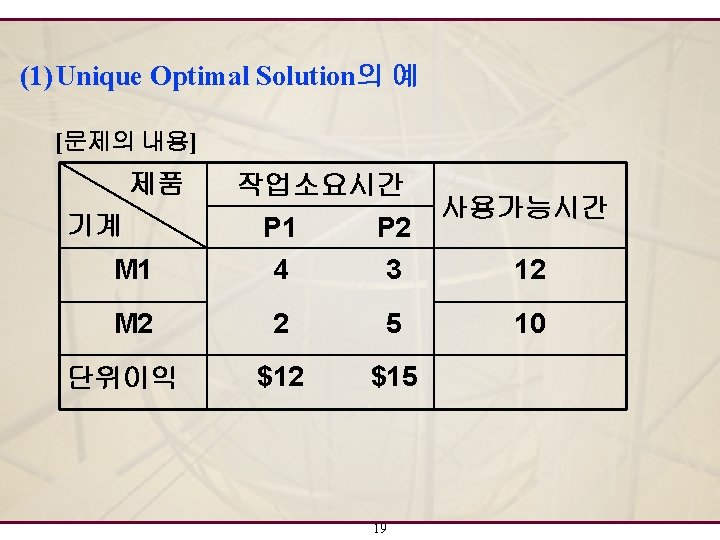
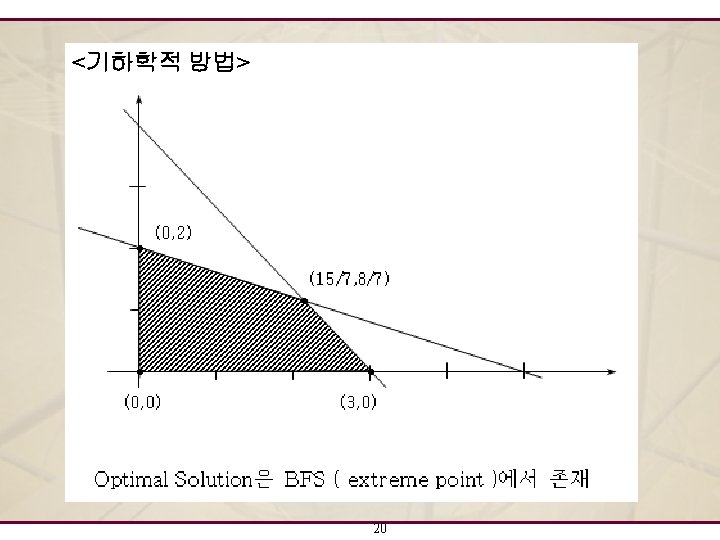

<Simplex 방법> 21
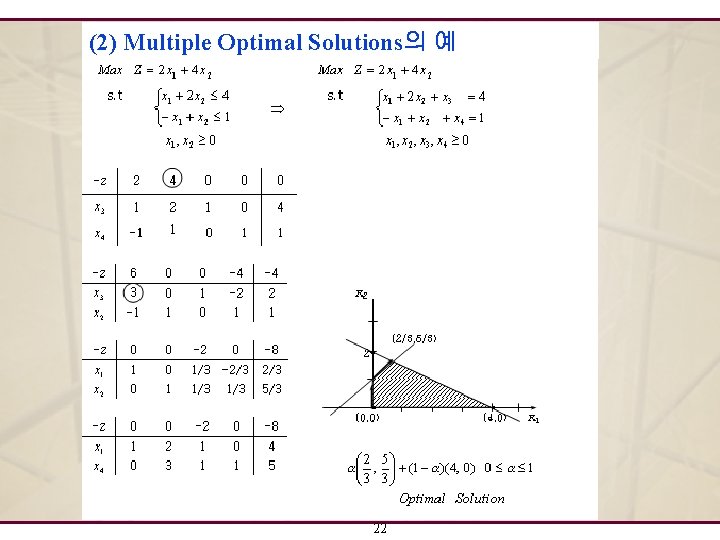
(2) Multiple Optimal Solutions의 예 22

(3) Unbounded Optimal Solutions의 예 23
- Slides: 23