Linear Programming Introductory Example THE PROBLEM A factory

Linear Programming : Introductory Example THE PROBLEM A factory produces two types of drink, an ‘energy’ drink and a ‘refresher’ drink. The day’s output is to be planned. Each drink requires syrup, vitamin supplement and concentrated flavouring, as shown in the table. The last row in the table shows how much of each ingredient is available for the day’s production. How can the factory manager decide how much of each drink to make?

THE PROBLEM Syrup Vitamin supplement Concentrated flavouring 5 litres of energy drink 1. 25 litres 2 units 30 cc 5 litres of refresher drink 1. 25 litres 1 unit 20 cc Availabilities 250 litres 300 units 4. 8 litres Energy drink sells at £ 1 per litre Refresher drink sells at 80 p per litre

FORMULATION Syrup constraint: Let x represent number of litres of energy drink Let y represent number of litres of refresher drink 0. 25 x + 0. 25 y 250 x + y 1000

FORMULATION Vitamin supplement constraint: Let x represent number of litres of energy drink Let y represent number of litres of refresher drink 0. 4 x + 0. 2 y 300 2 x + y 1500

FORMULATION Concentrated flavouring constraint: Let x represent number of litres of energy drink Let y represent number of litres of refresher drink 6 x + 4 y 4800 3 x + 2 y 2400

FORMULATION Objective function: Let x represent number of litres of energy drink • Energy drink sells for £ 1 per litre Let y represent number of litres of refresher drink • Refresher drink sells for 80 pence per litre Maximise x + 0. 8 y

SOLUTION Empty grid to accommodate the 3 inequalities

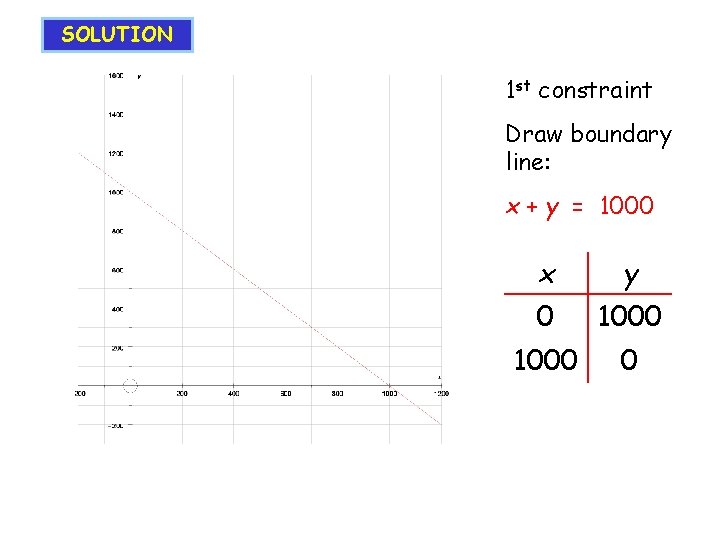
SOLUTION 1 st constraint Draw boundary line: x + y = 1000 x y 0 1000 0

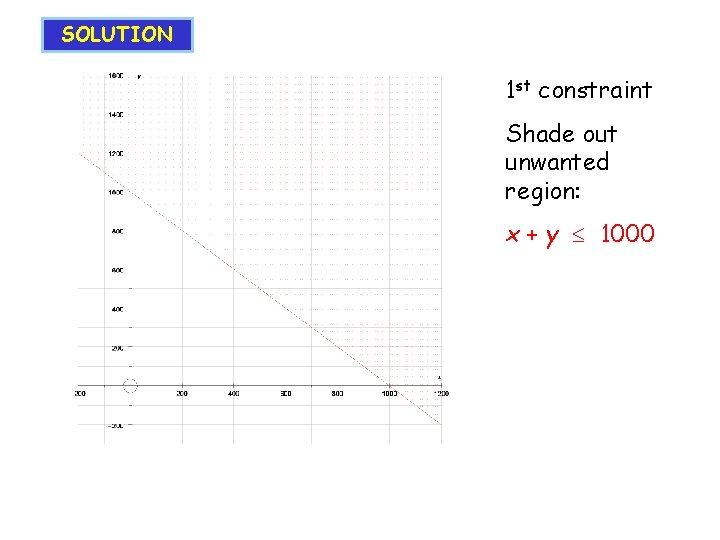
SOLUTION 1 st constraint Shade out unwanted region: x + y 1000

SOLUTION Empty grid to accommodate the 3 inequalities

SOLUTION 2 nd constraint Draw boundary line: 2 x + y = 1500 x y 0 1500 750 0

SOLUTION 2 nd constraint Shade out unwanted region: 2 x + y 1500

SOLUTION Empty grid to accommodate the 3 inequalities

SOLUTION 3 rd constraint Draw boundary line: 3 x + 2 y = 2400 x y 0 1200 800 0

SOLUTION 3 rd constraint Shade out unwanted region: 3 x + 2 y 2400

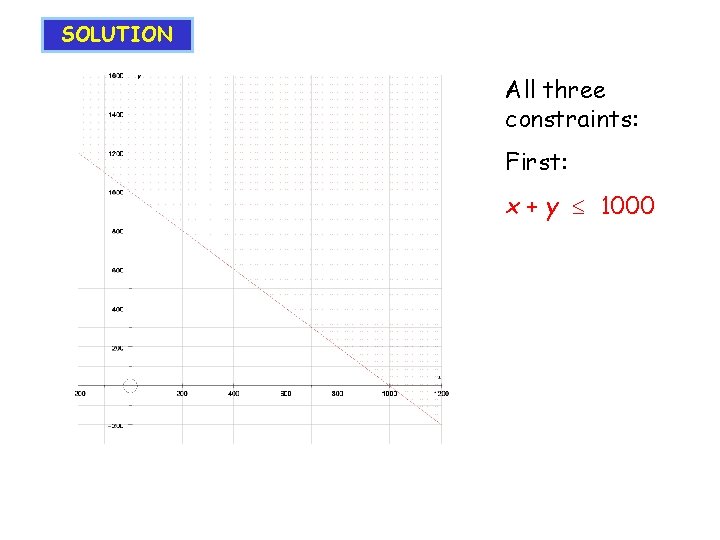
SOLUTION All three constraints: First: x + y 1000

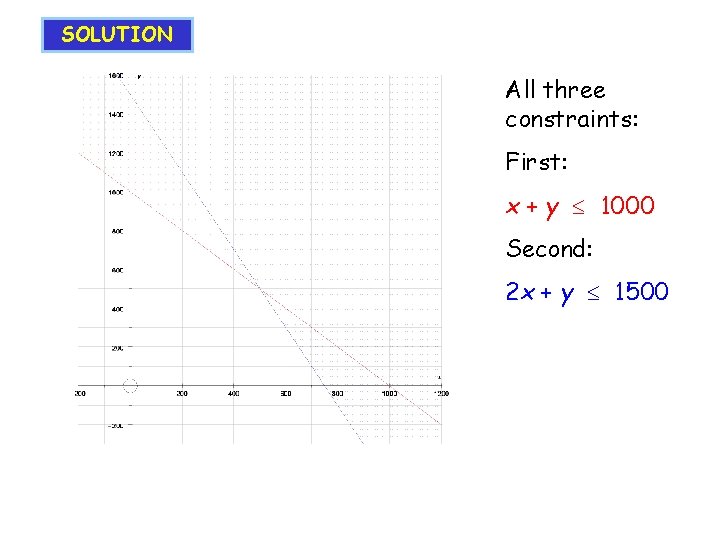
SOLUTION All three constraints: First: x + y 1000 Second: 2 x + y 1500

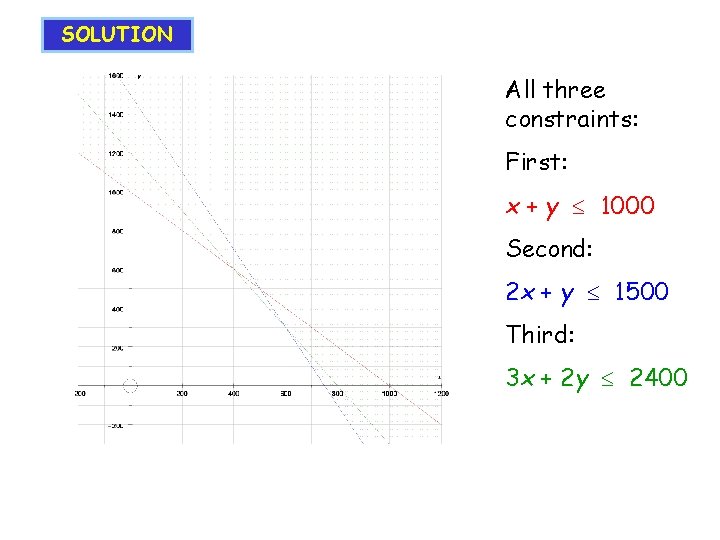
SOLUTION All three constraints: First: x + y 1000 Second: 2 x + y 1500 Third: 3 x + 2 y 2400

SOLUTION All three constraints: First: x + y 1000 Second: 2 x + y 1500 Third: 3 x + 2 y 2400 Adding: x 0 and y 0

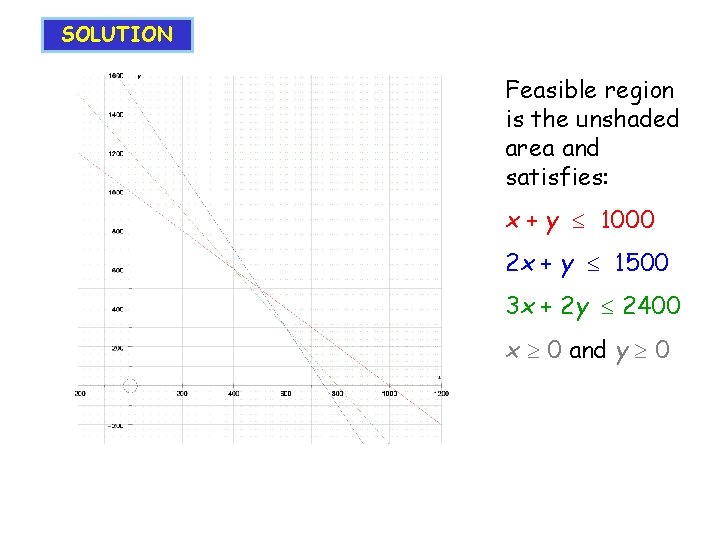
SOLUTION Feasible region is the unshaded area and satisfies: x + y 1000 2 x + y 1500 3 x + 2 y 2400 x 0 and y 0

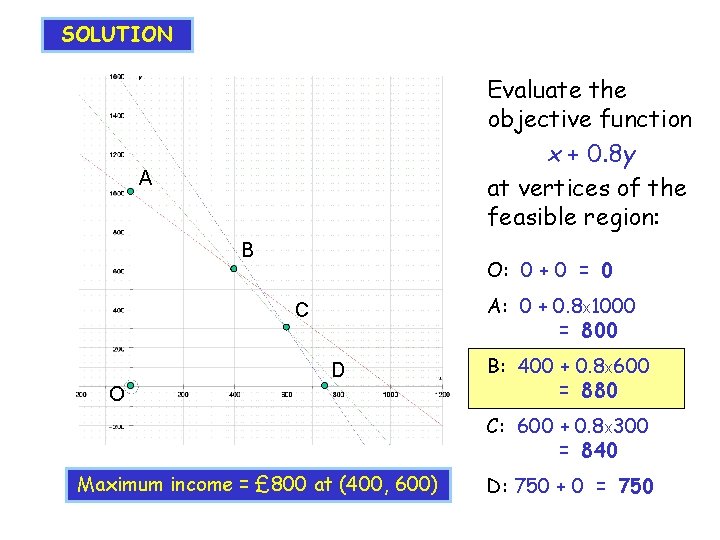
SOLUTION Evaluate the objective function x + 0. 8 y at vertices of the feasible region: A B O: 0 + 0 = 0 A: 0 + 0. 8 x 1000 = 800 C D O B: 400 + 0. 8 x 600 = 880 C: 600 + 0. 8 x 300 = 840 Maximum income = £ 800 at (400, 600) D: 750 + 0 = 750