Linear Programming GENERAL MATHS UNIT TWO Review Sketching














































- Slides: 78

Linear Programming GENERAL MATHS – UNIT TWO

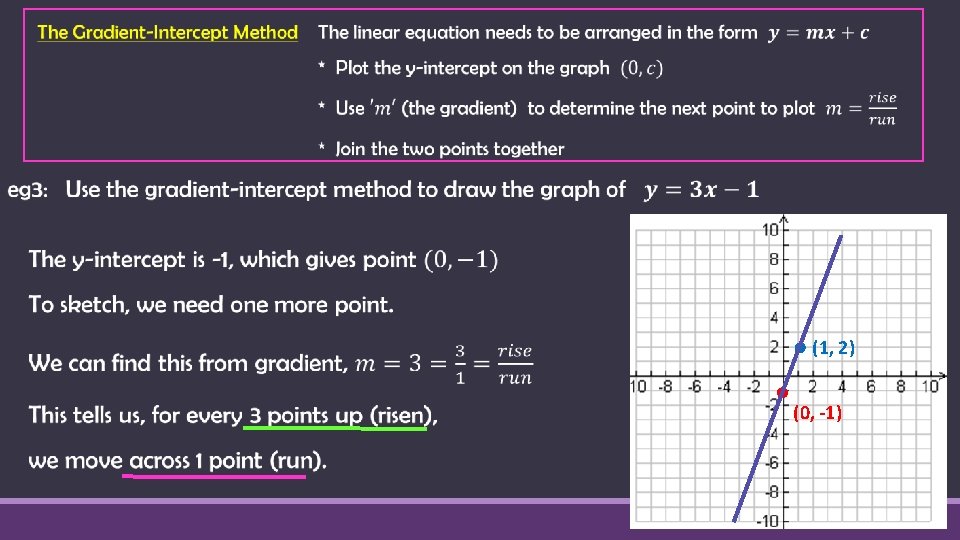
Review - Sketching Linear Graphs




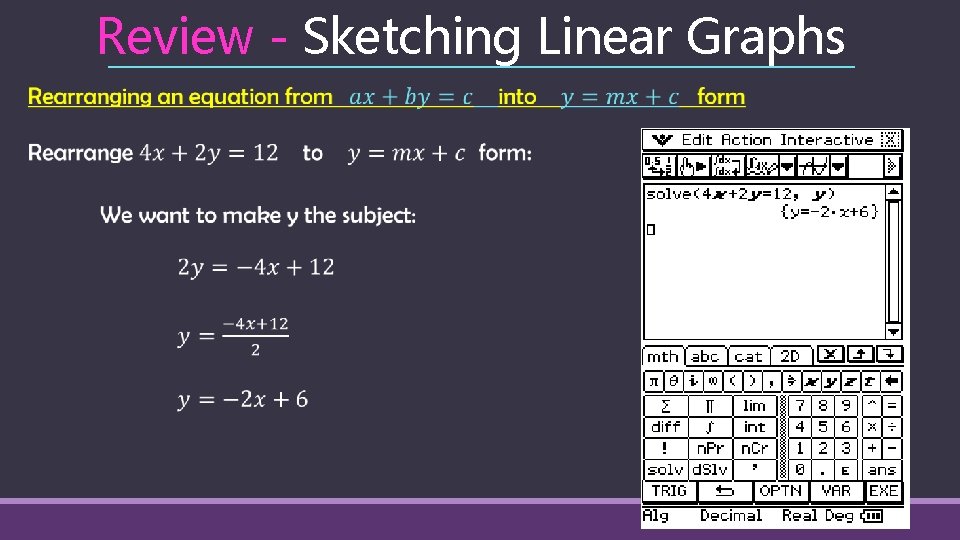
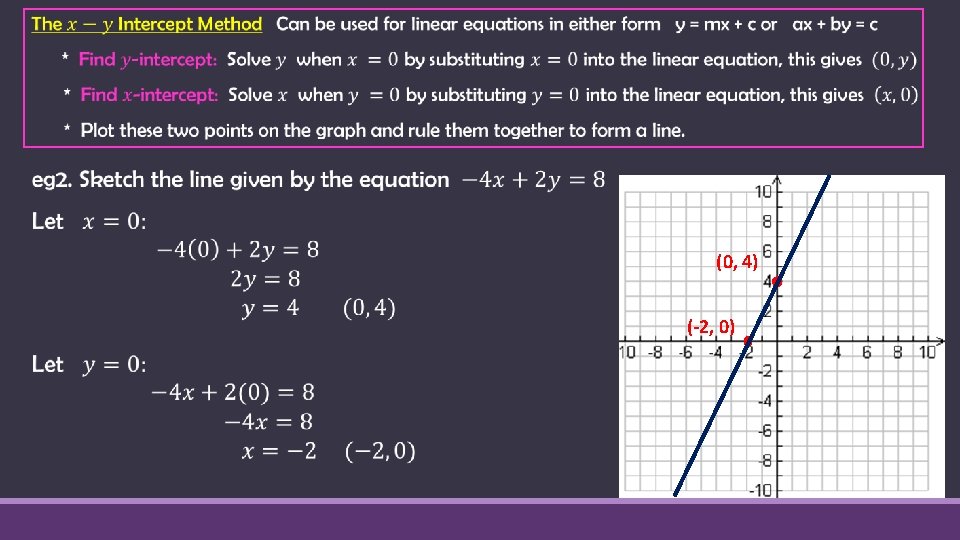
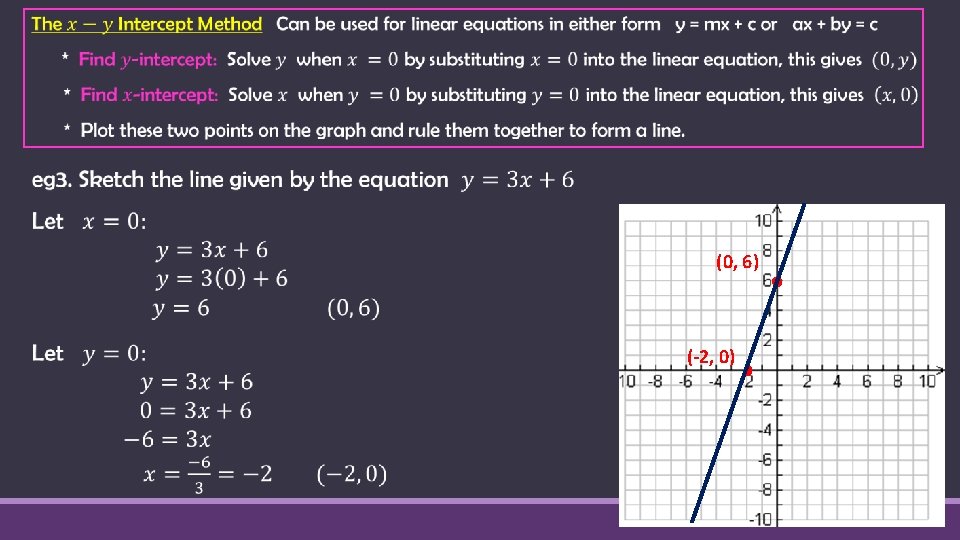
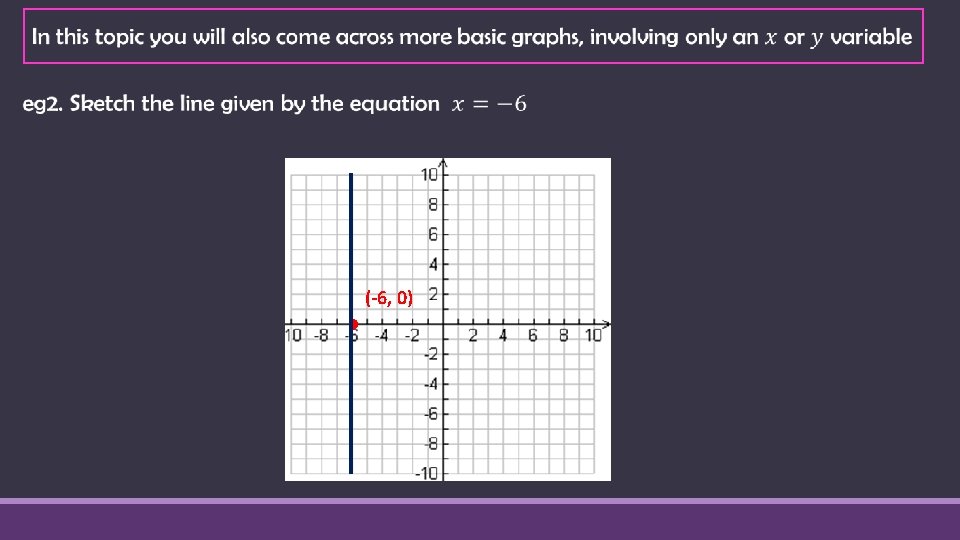
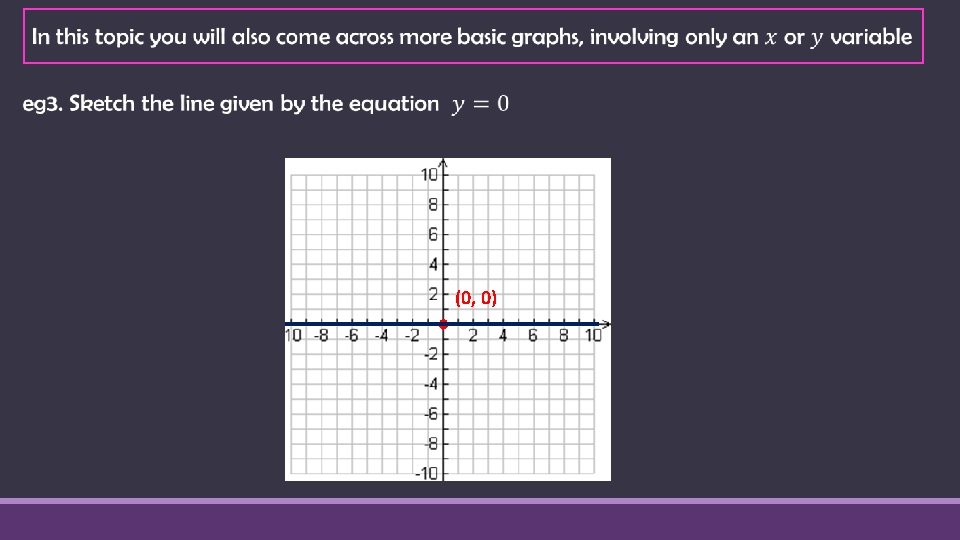
Review - Sketching Linear Graphs

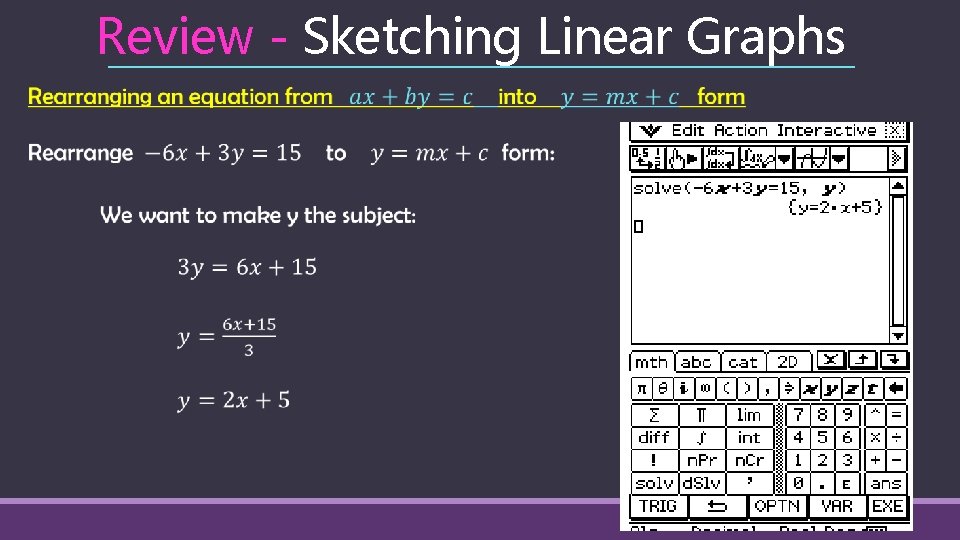
Review - Sketching Linear Graphs

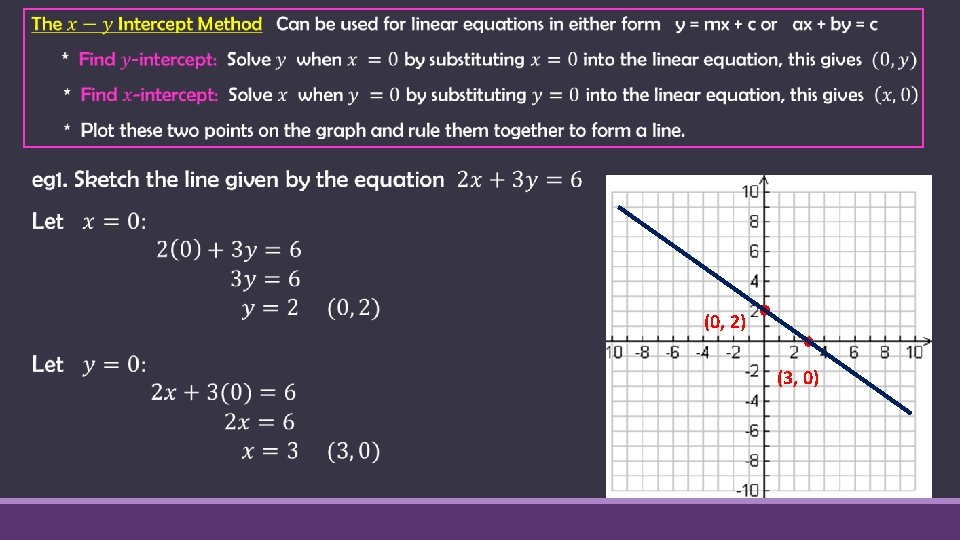
Review - Sketching Linear Graphs







Now Try Worksheet One Page One

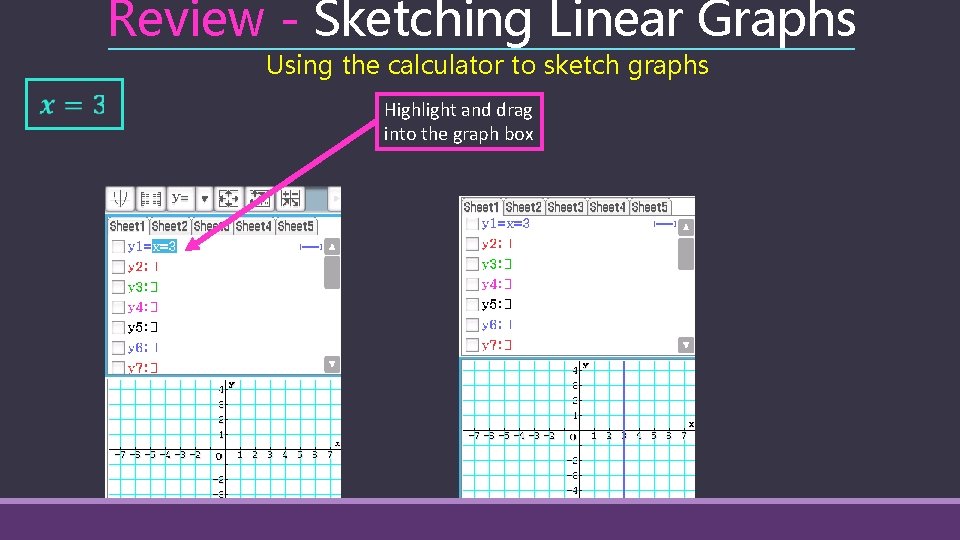
Review - Sketching Linear Graphs Using the calculator to sketch graphs Highlight and drag into the graph box

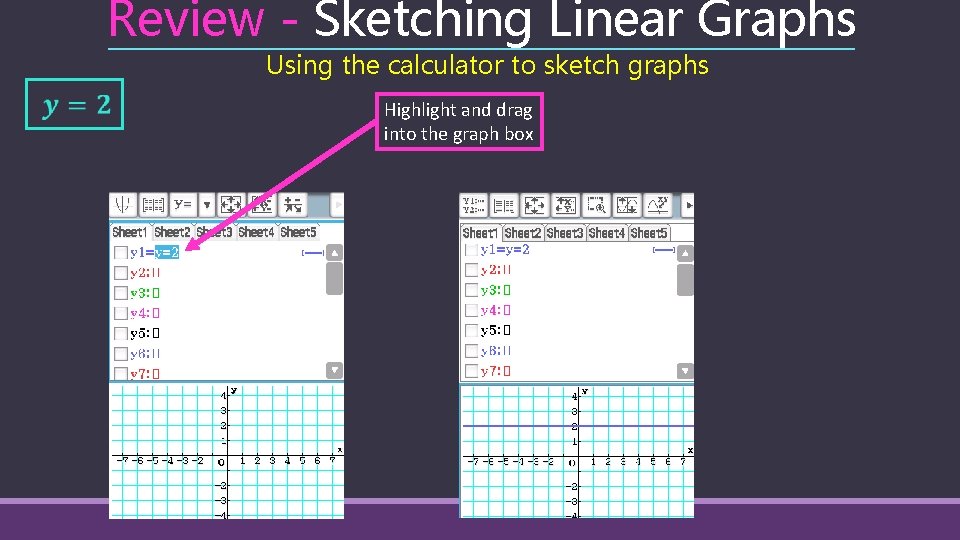
Review - Sketching Linear Graphs Using the calculator to sketch graphs Highlight and drag into the graph box

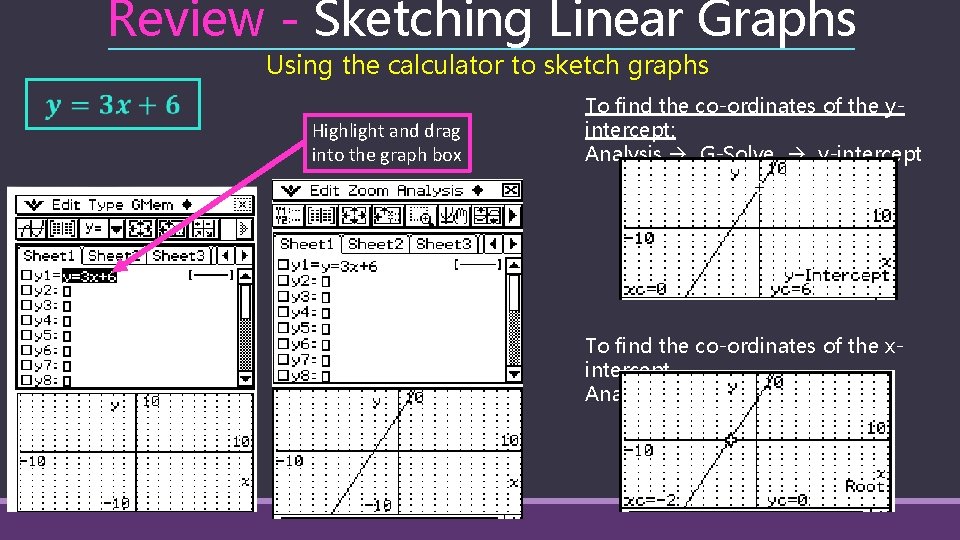
Review - Sketching Linear Graphs Using the calculator to sketch graphs Highlight and drag into the graph box To find the co-ordinates of the yintercept: Analysis G-Solve y-intercept To find the co-ordinates of the xintercept Analysis G-Solve root

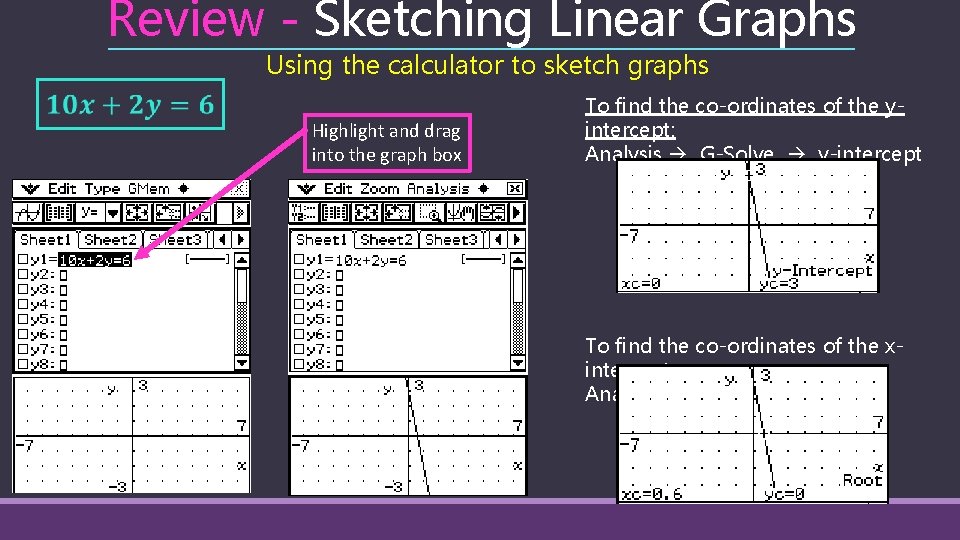
Review - Sketching Linear Graphs Using the calculator to sketch graphs Highlight and drag into the graph box To find the co-ordinates of the yintercept: Analysis G-Solve y-intercept To find the co-ordinates of the xintercept Analysis G-Solve root

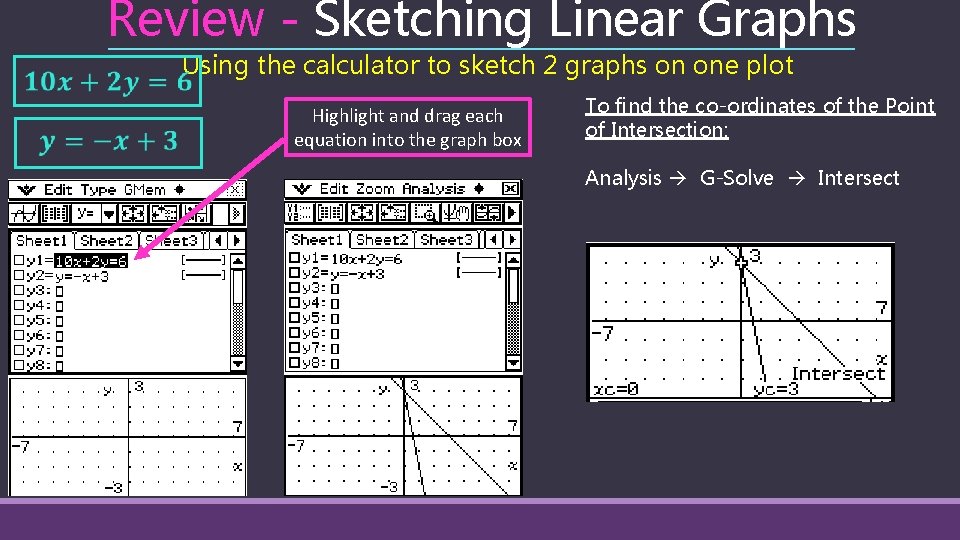
Review - Sketching Linear Graphs Using the calculator to sketch 2 graphs on one plot Highlight and drag each equation into the graph box To find the co-ordinates of the Point of Intersection: Analysis G-Solve Intersect

Now: Then: Check your answers to the worksheet using your calculator Do the other side of the page

Understanding Inequalities less than greater than less than or equal to greater than or equal to

Understanding Inequalities 0 1 2 3 4 5 6 7 8 9 10

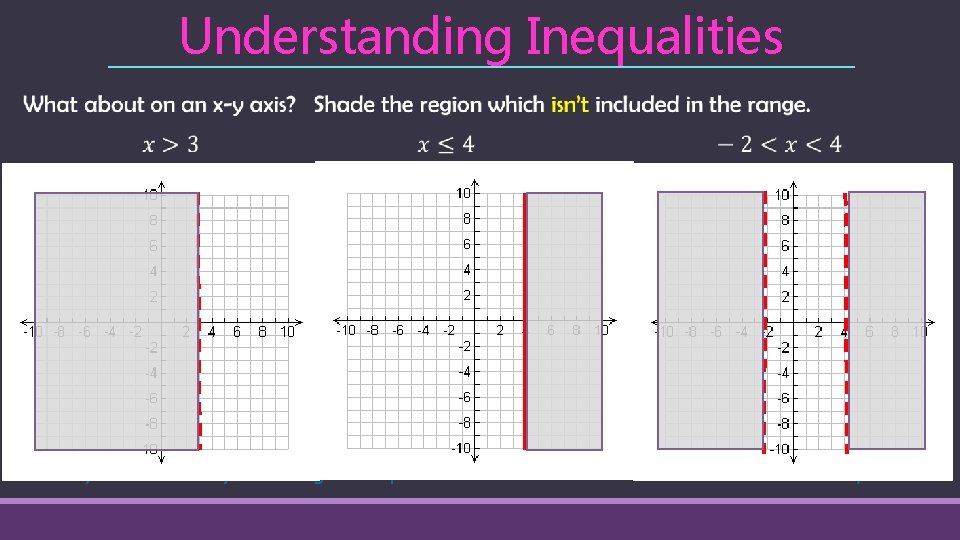
Understanding Inequalities

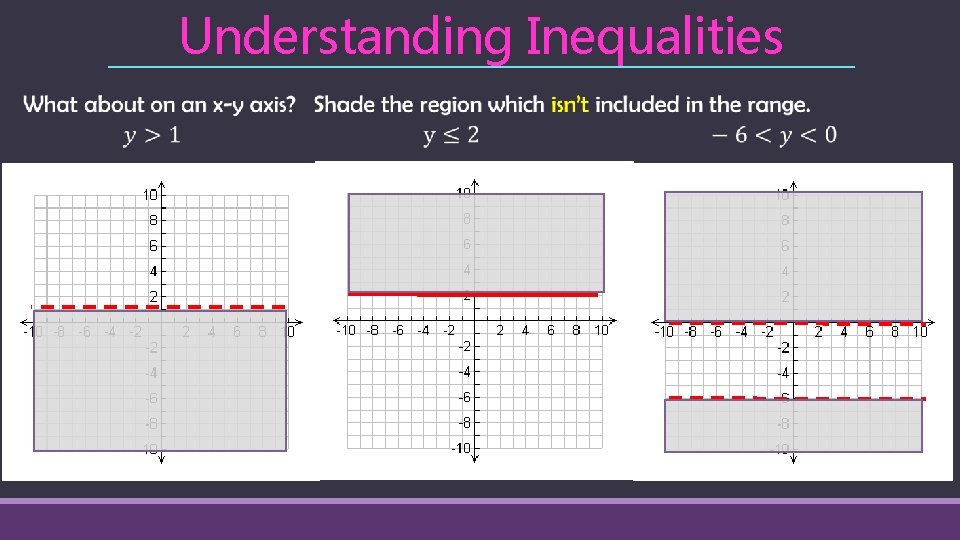
Understanding Inequalities

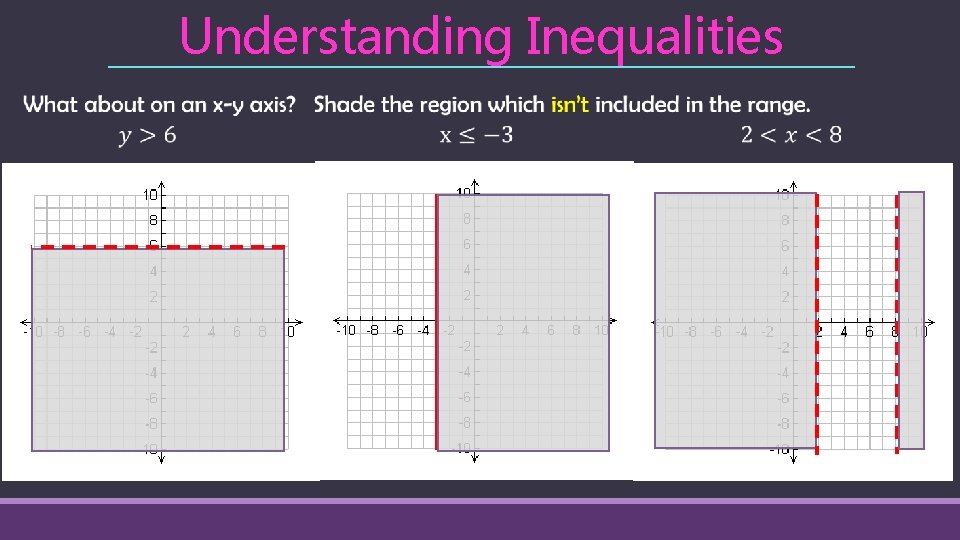
Understanding Inequalities

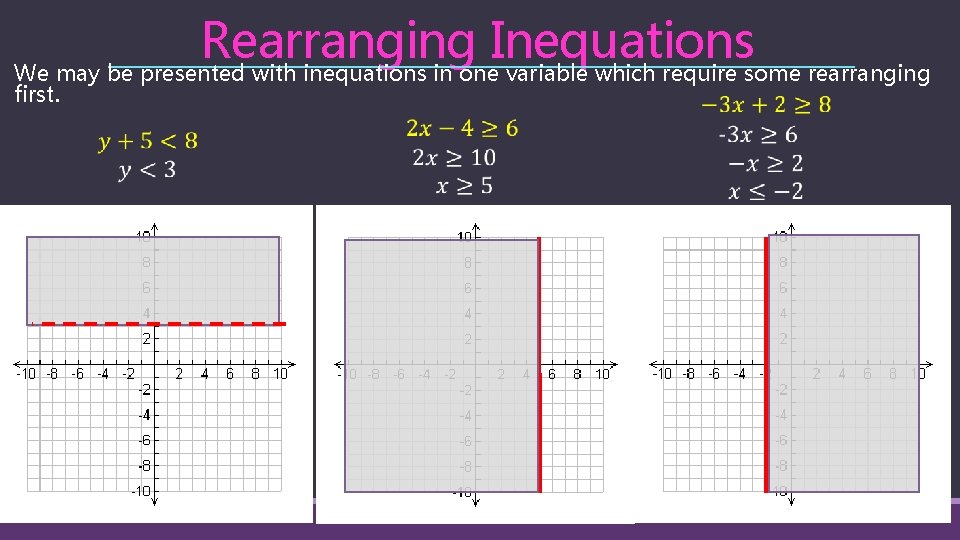
Rearranging Inequations We may be presented with inequations in one variable which require some rearranging first.

Now Try Exercise 11. 2 Questions 1, 2, 3, 4, 7

Is this true? YES

YES Is this true?

Is this true? NO

Is this true? NO

Is this true? YES

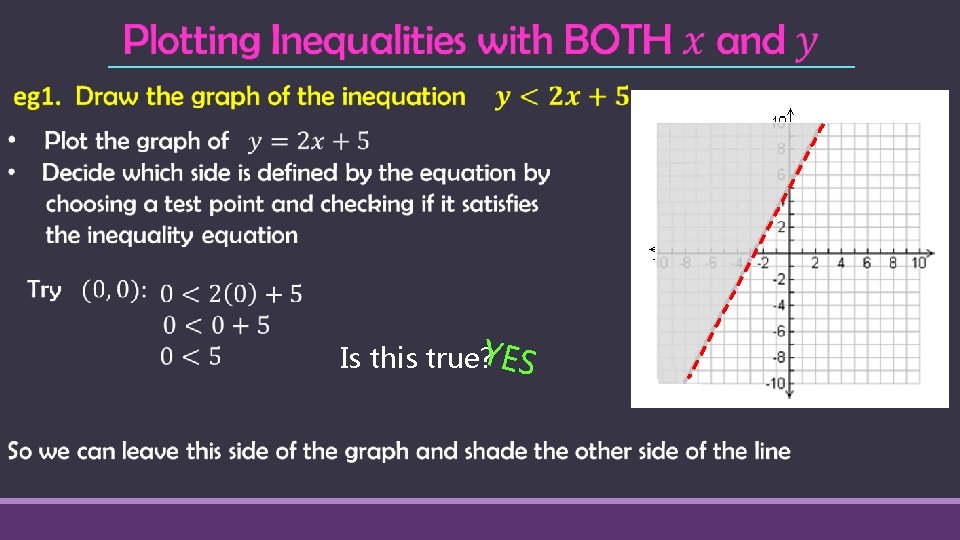
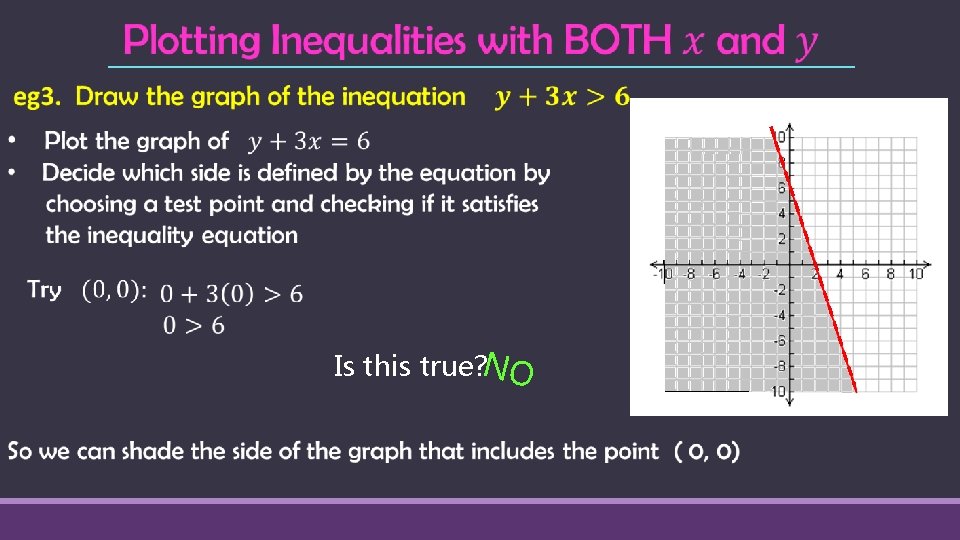
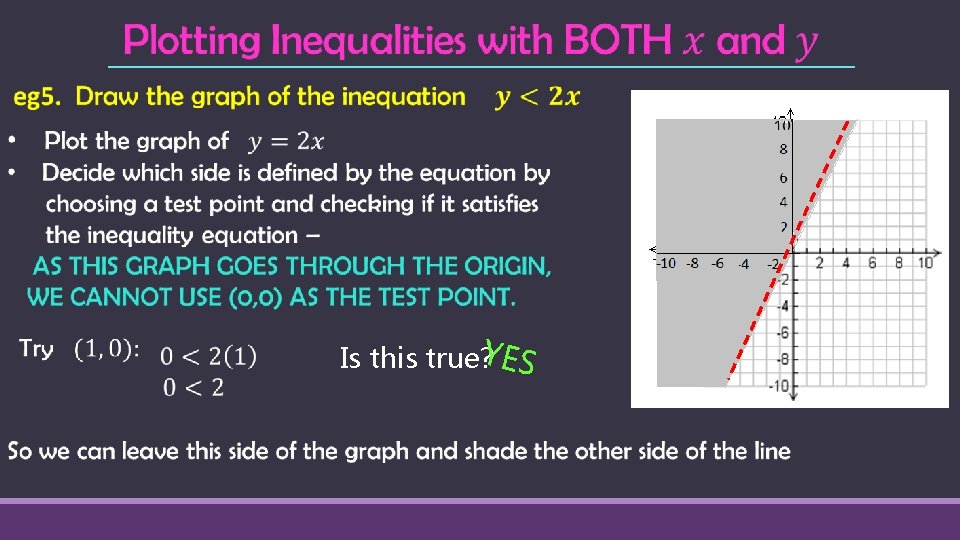
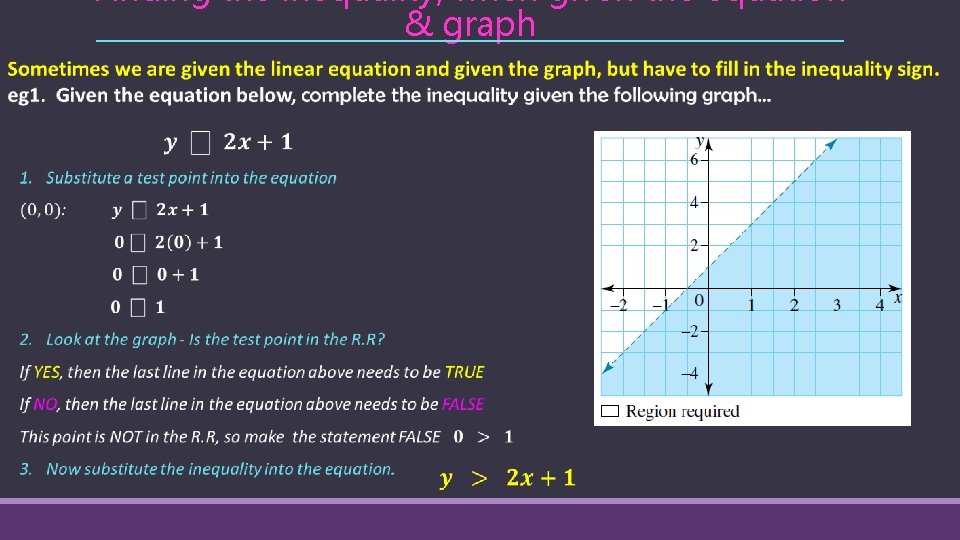
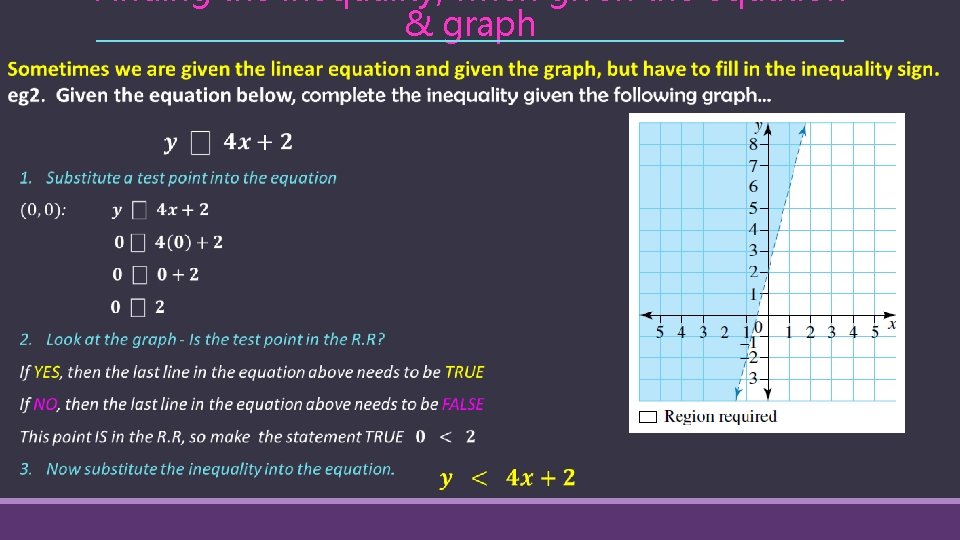
Finding the inequality, when given the equation & graph

Finding the inequality, when given the equation & graph

Now Try Exercise 11. 2 Questions 5, 6, 8, 9, 10, 11, 13, 16

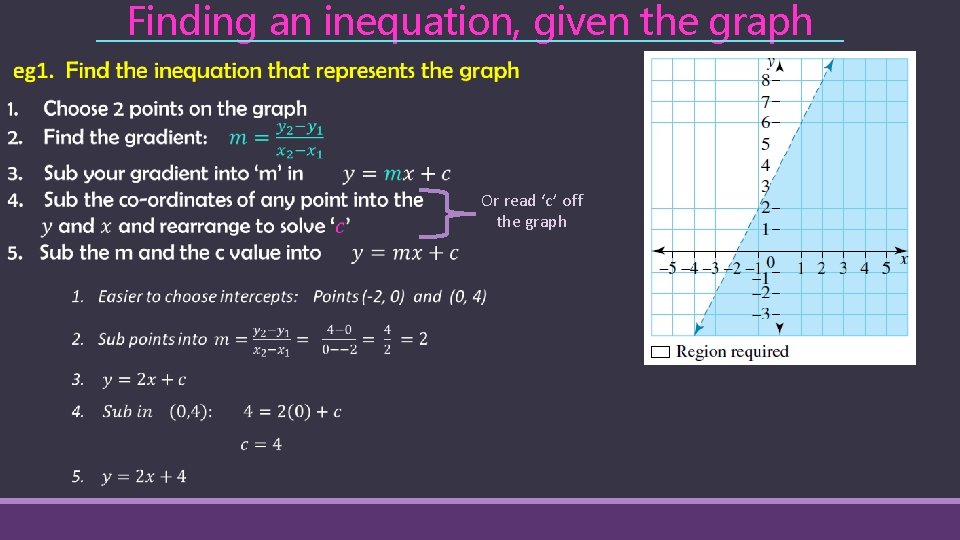
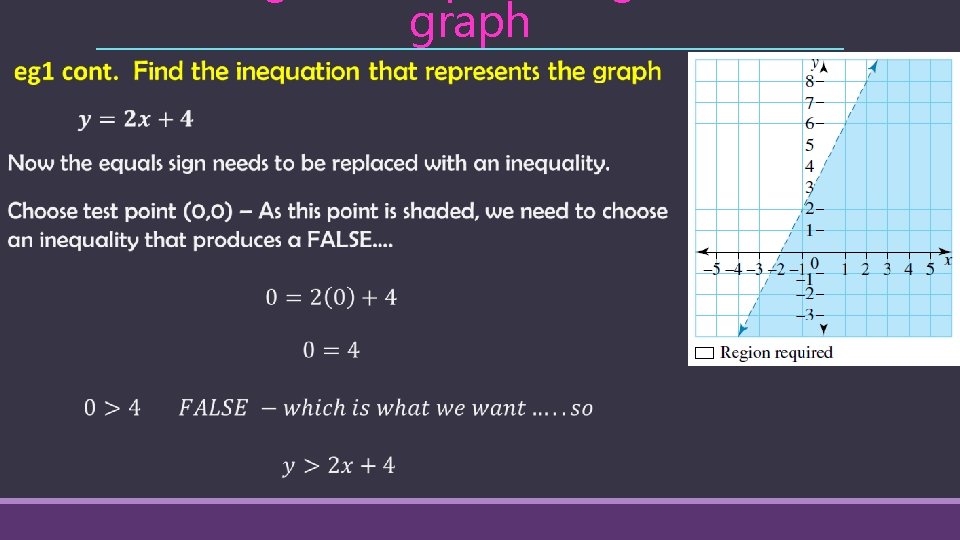
Finding an inequation, given the graph Or read ‘c’ off the graph

graph

Now Try Exercise 11. 2 Questions 5, 6, 8, 9, 10, 11, 13, 16, 17 b, 18 a

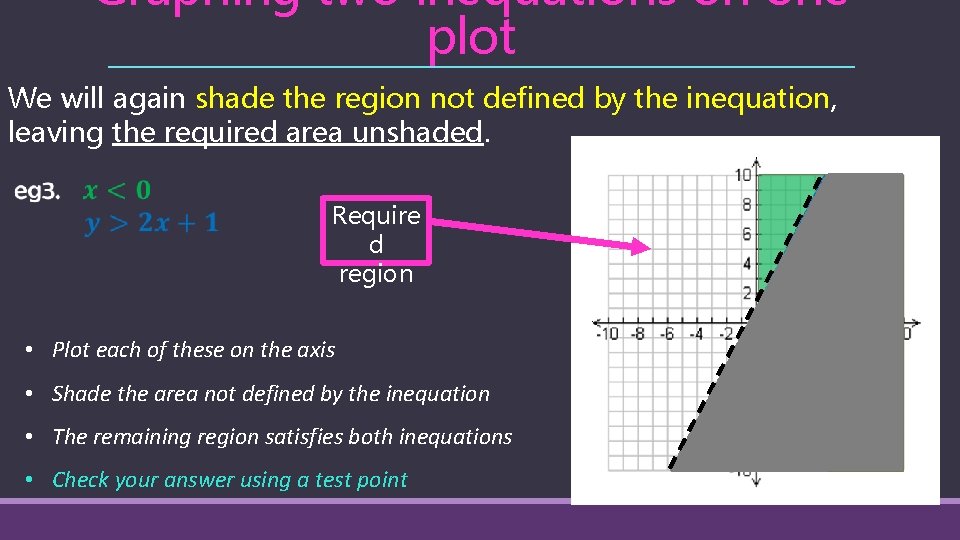
Graphing two inequations on one plot We plot 2 inequations on the same axis & find the region which satisfies both inequations. We will again shade the region not defined by the inequation, leaving the required area unshaded. Require d region • Plot each of these on the axis • Shade the area not defined by the inequation • The remaining region satisfies both inequations

Graphing two inequations on one plot We will again shade the region not defined by the inequation, leaving the required area unshaded. Require d region • Plot each of these on the axis • Shade the area not defined by the inequation • The remaining region satisfies both inequations

Graphing two inequations on one plot We will again shade the region not defined by the inequation, leaving the required area unshaded. Require d region • Plot each of these on the axis • Shade the area not defined by the inequation • The remaining region satisfies both inequations • Check your answer using a test point

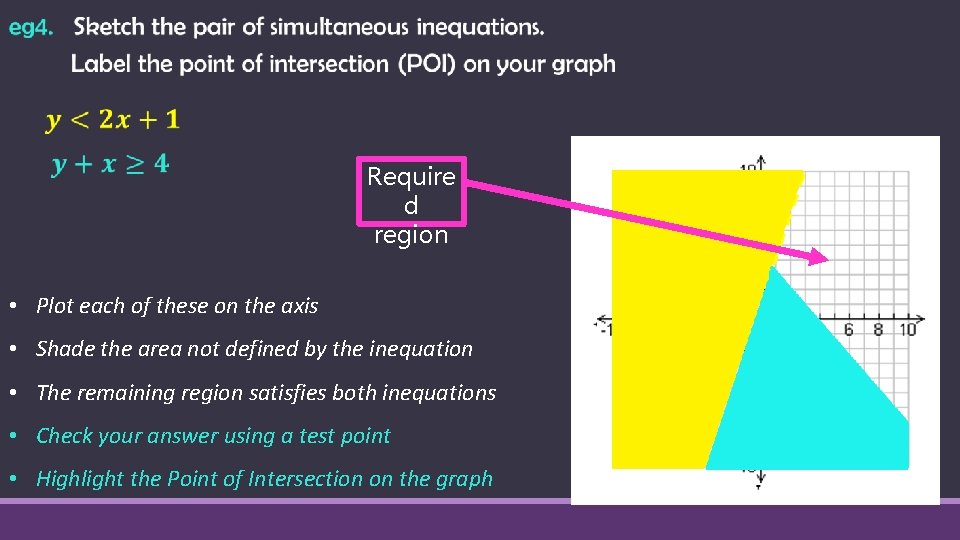
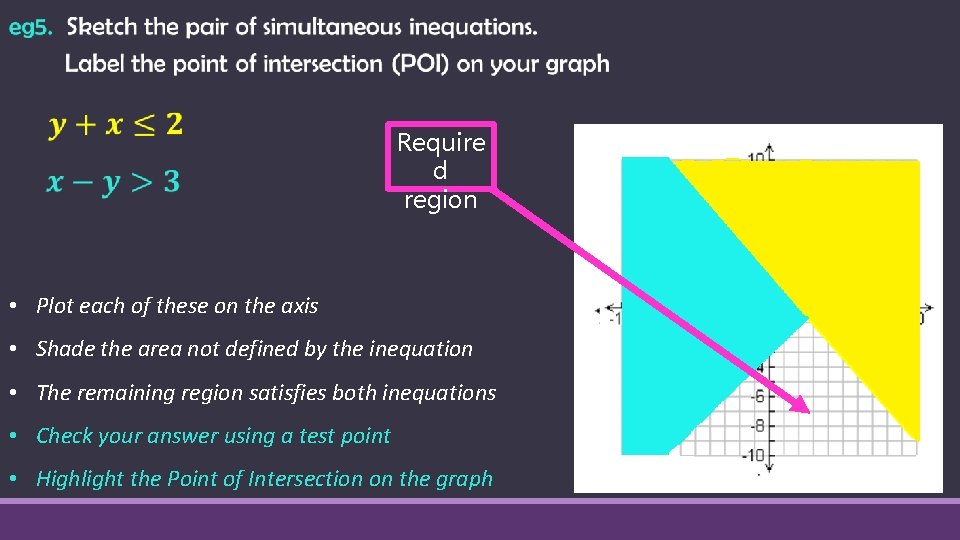
Require d region • Plot each of these on the axis • Shade the area not defined by the inequation • The remaining region satisfies both inequations • Check your answer using a test point • Highlight the Point of Intersection on the graph

Require d region • Plot each of these on the axis • Shade the area not defined by the inequation • The remaining region satisfies both inequations • Check your answer using a test point • Highlight the Point of Intersection on the graph

Now Try Exercise 11. 3 Questions 1, 2, 3, 4, 11, 12, 14

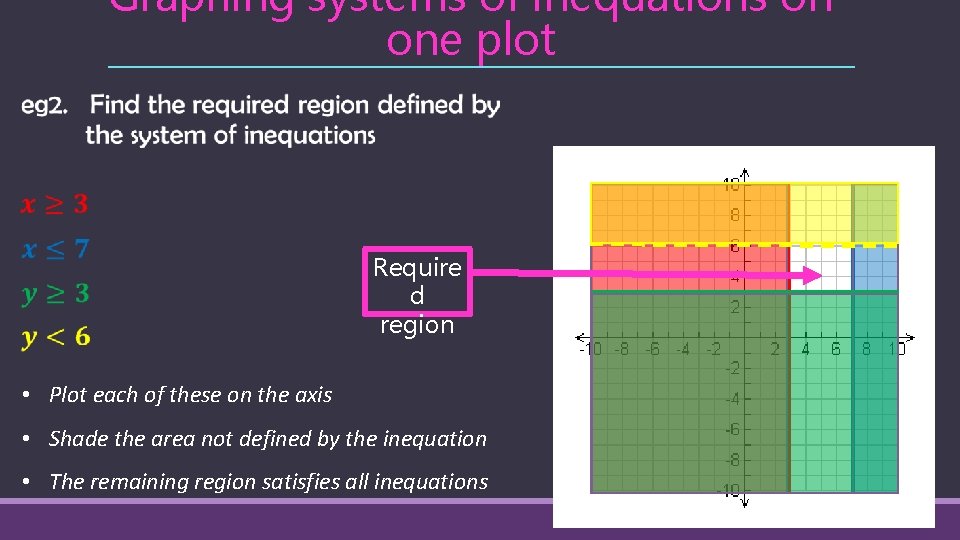
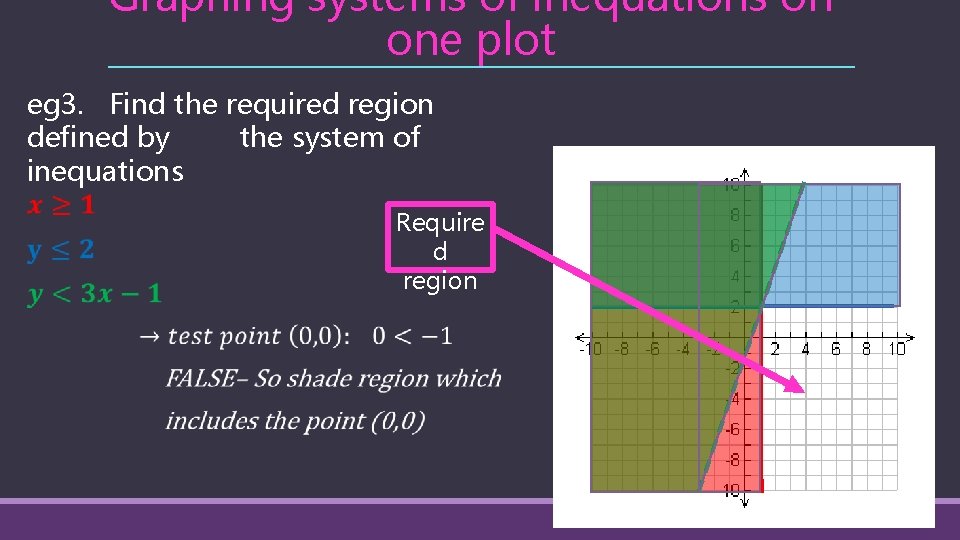
Graphing systems of inequations on one plot We will again shade the region not defined by the inequation, leaving the required area unshaded. Require d region • Plot each of these on the axis • Shade the area not defined by the inequation • The remaining region satisfies all inequations

Graphing systems of inequations on one plot Require d region • Plot each of these on the axis • Shade the area not defined by the inequation • The remaining region satisfies all inequations

Graphing systems of inequations on one plot eg 3. Find the required region defined by the system of inequations Require d region

Graphing systems of inequations on one plot eg 4. Find the required region defined by the system of inequations Require d region

Now try Worksheet 2 then Exercise 11. 3 Questions 1, 2, 3, 4, 11, 12, 14

Linear Programming Applications: Solving worded problems These problems involve converting worded problems into a series of linear inequations. Using the corner points of the feasible region, we can solve real problems involving finding a maximum or minimum number – ie. Finding a maximum profit, or a minimum Cost. Objective function is the Profit or Cost equation that we are trying to maximise or minimise. Constraints are the linear inequations we create and sketch to find the feasible region. Constraints may include things like the amount of material we have to

Worded Problems: Forming constraints eg 1. A bakery makes two varieties of cake – Mud Cake and Cheesecake. One batch of mud cakes take 1 hour of labour to produce. One batch of cheesecakes takes 1. 5 hours of labour to produce. A total of 40 hours of labour is available each week. They must produce a minimum of 10 batches of mud cakes and 8 batches of cheesecakes. Define the constraints for this problem and sketch the feasible region for producing cakes. 1. Define to variables to solve your question: 2. Define the Constraints:

1. Define to variables to solve your question: 2. Define the Constraints: 3. Plot the constraints and find the feasible region:

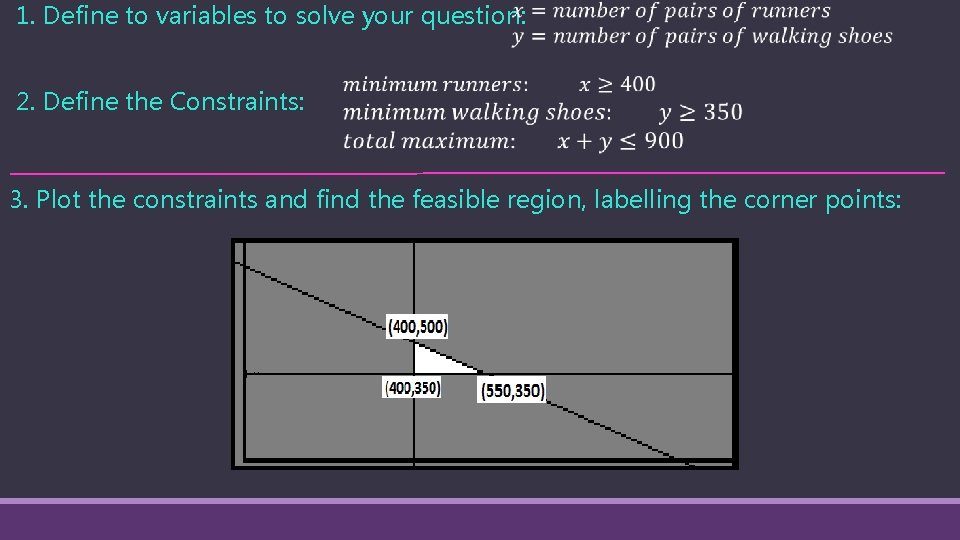
Worded Problems: Forming constraints eg 2. A local factory produces runners and walking shoes. It is able to produce a minimum of 400 pairs of runners and 350 pairs of walking shoes. The factory is capable of producing a maximum of 900 pairs of shoes altogether. Define the constraints for this problem and sketch the feasible region. 1. Define to variables to solve your question: 2. Define the Constraints:

1. Define to variables to solve your question: 2. Define the Constraints: 3. Plot the constraints and find the feasible region, labelling the corner points:

Worded Problems: Forming constraints eg 3. A farmer has a plot of 35 hectare plot of land to plant oats and wheat. Oats require 3 hours of labour to produce per hectare. Wheat require 4 hours of labour to produce per hectare. A total of 120 hours of labour is available. Define the constraints for this problem and sketch the feasible region. 1. Define to variables to solve your question: 2. Define the Constraints:

1. Define to variables to solve your question: 2. Define the Constraints: 3. Plot the constraints and find the feasible region:

Now Try Exercise 11. 3 Questions 5, 6, 15, 17

Worded Problems: Forming Objective Functions The objective of a problem, is what we are hoping to achieve, usually to minimize costs or maximize profits. You will be given information to allow you to form the Objective Function. Eg. Gemma makes necklaces and bracelets. She makes a profit of $5 on each necklace and $4 for each bracelet that she sells. Write an equation to find her maximum profit. 1. Define variables: 2. Determine what is to be maximized or minimized: 3. Write the objective function:

Worded Problems: Forming Objective Functions Eg 2. Reece owns a clothing store. His best selling items are jeans and watches. He purchases these from a wholesaler, jeans for $80 and watches for $70. Write an objective function to minimize his costs. 1. Define variables: 2. Determine what is to be maximized or minimized: 3. Write the objective function:

Worded Problems: Forming Objective Functions Eg 2. A stationery manufacturer makes two types of products: rulers and erasers. It costs the manufacturer $0. 10 to make the rulers and $0. 05 to make the erasers. The manufacturer sells its products to the distributors who buy the rulers for $0. 12 and the erasers for $0. 08. Write an equation to find the manufacturer’s minimum cost and maximum profit (two objective functions). 1. Define variables: 2. Determine what is to be maximized or minimized: 3. Write the objective functions:

Now Try Exercise 11. 3 Questions 5, 6, 7, 15, 16, 17, 19

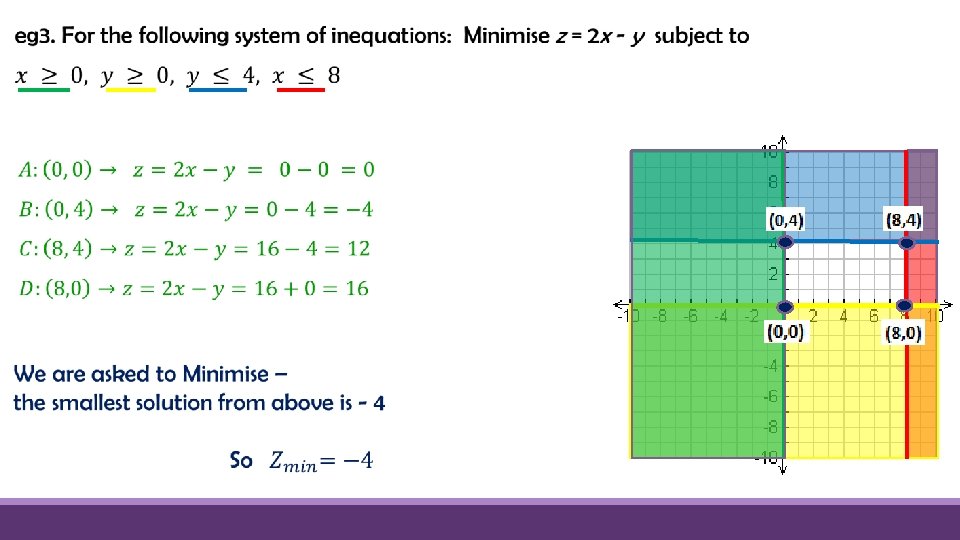
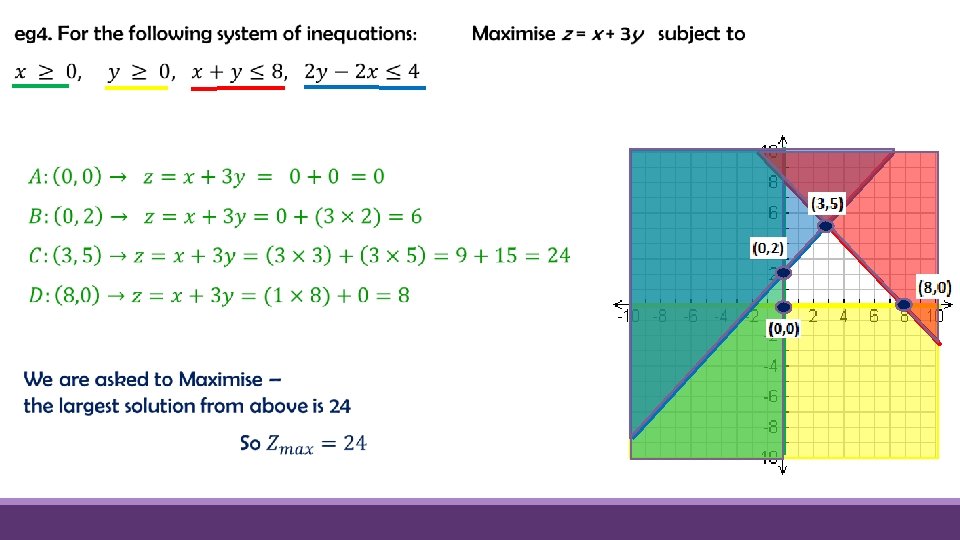
Maximising and minimising linear functions Using linear programming, we can maximise or minimise linear functions subject to constraints given by a set of linear inequations. Today we will do this using the corner point method, using the following steps: 1. Sketch the feasible region 2. Determine the coordinates of the corner points of the feasible region 3. Substitute the coordinates of the corner points into the given objective function (the linear equation to be maximised or minimised)

1. 2. 3. Sketch the feasible region Determine the coordinates of the corner points of the feasible region Sub. the corner points into the objective function (the linear equation to be maximised or minimised) 4. Choose which set of coordinates produces the maximum or minimum value, as stated in the question Require d region Corner Points (0, 1) (0, 8) (6, 1) (6, 8)

1. 2. 3. Sketch the feasible region Determine the coordinates of the corner points of the feasible region Sub. the corner points into the objective function (the linear equation to be maximised or minimised) 4. Choose which set of coordinates produces the maximum or minimum value, as stated in the question Require d region Corner Points (0, 3) (0, 10) (4, 3) (4, 10)

1. 2. 3. Sketch the feasible region Determine the coordinates of the corner points of the feasible region Sub. the corner points into the objective function (the linear equation to be maximised or minimised) 4. Choose which set of coordinates produces the maximum or minimum value, as stated in the question Require d region Corner Points (0, 0) (0, 4) (4, 0)

1. 2. 3. Sketch the feasible region Determine the coordinates of the corner points of the feasible region Sub. the corner points into the objective function (the linear equation to be maximised or minimised) 4. Choose which set of coordinates produces the maximum or minimum value, as stated in the question Require d region Corner Points (2, 0) (0, -6) (6, -6)

Now Try Worksheet Maximum/Minimum Problems Then: Exercise 11. 4: Q 8, 1, 2

Worksheet Solutions





Linear Programming Applications: Solving worded problems eg 1. A local factory produces runners and walking shoes. It is able to produce a minimum of 400 pairs of runners and 350 pairs of walking shoes. The factory is capable of producing a maximum of 900 pairs of shoes altogether. The profit on a pair of runners is $12. 50 and on a pair of walking shoes, $10. What combination of shoes should the factory make to maximise profits? 1. Define to variables to solve your question: 2. Define the Objective Function: 3. Define the Constraints:

1. Define to variables to solve your question: 2. Define the Objective Function: 3. Define the Constraints: 7. Answer the question given in the initial pro We want to maximise profit, so if 550 pairs of runners and 350 pairs of walkers are produced and sold, the company makes a profit of $10375

Linear Programming Applications: Solving worded problems eg 2. A farmer has a plot of 35 hectare plot of land to plant oats and wheat. Oats require 3 hours of labour to produce per hectare. Wheat require 4 hours of labour to produce per hectare. A total of 120 hours of labour is available. Profit on oats is $200 per hectare and wheat is $240 per hectare. What should he plant to maximise profits? 1. Define to variables to solve your question: 2. Define the Objective Function: 3. Define the Constraints:

1. Define to variables to solve your question: 2. Define the Objective Function: 3. Define the Constraints: 7. Answer the question given in the initial pro We want to maximise profit, so if 20 ha of oats and 15 ha of wheat is produced, the farmer will achieve a maximum profit of $7600

Now Try Exercise 11. 4 Q 5, 6, 7, 12, 13, 18