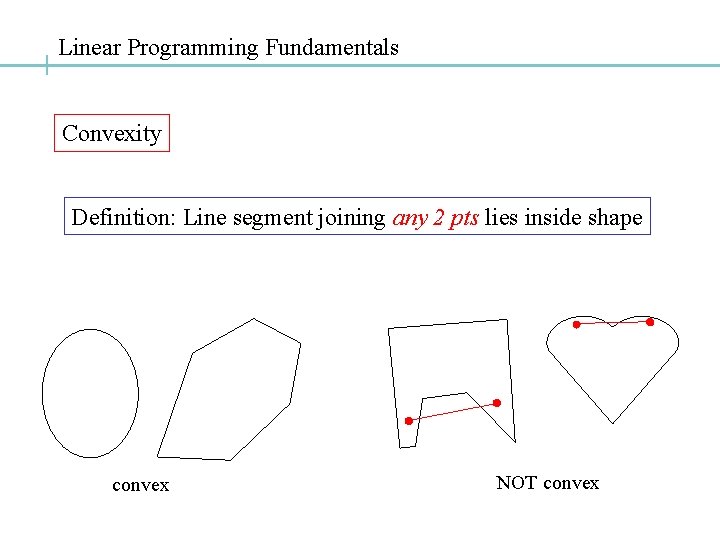
Linear Programming Fundamentals Convexity Definition Line segment joining

Linear Programming Fundamentals Convexity Definition: Line segment joining any 2 pts lies inside shape convex NOT convex

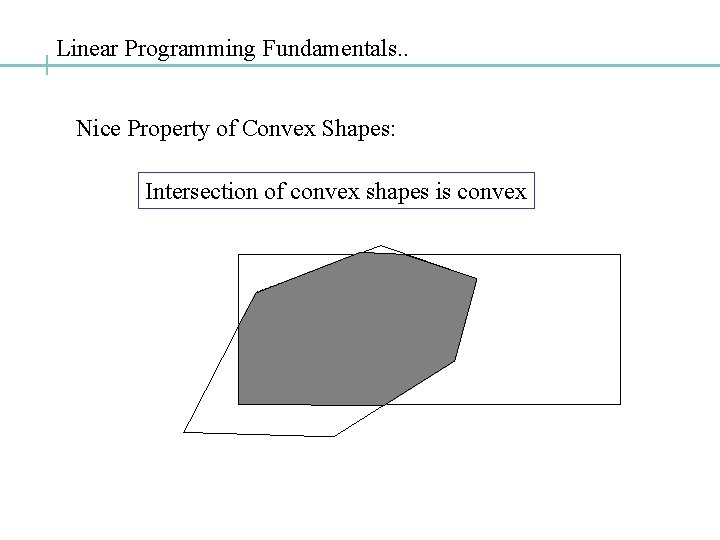
Linear Programming Fundamentals. . Nice Property of Convex Shapes: Intersection of convex shapes is convex

Linear Programming Fundamentals… Every Half-space is convex Each constraint of an LP half space Set of feasible solutions is a convex polyhedron

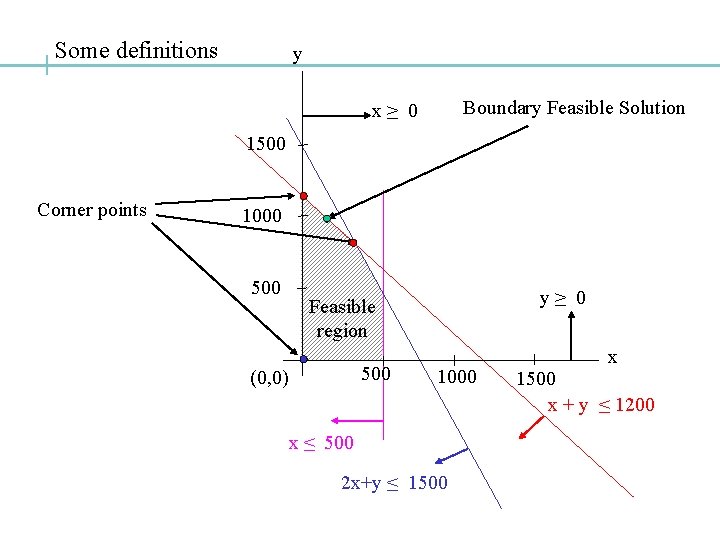
Some definitions y Boundary Feasible Solution x≥ 0 1500 Corner points 1000 500 y≥ 0 Feasible region 500 (0, 0) 1000 x ≤ 500 2 x+y ≤ 1500 x + y ≤ 1200

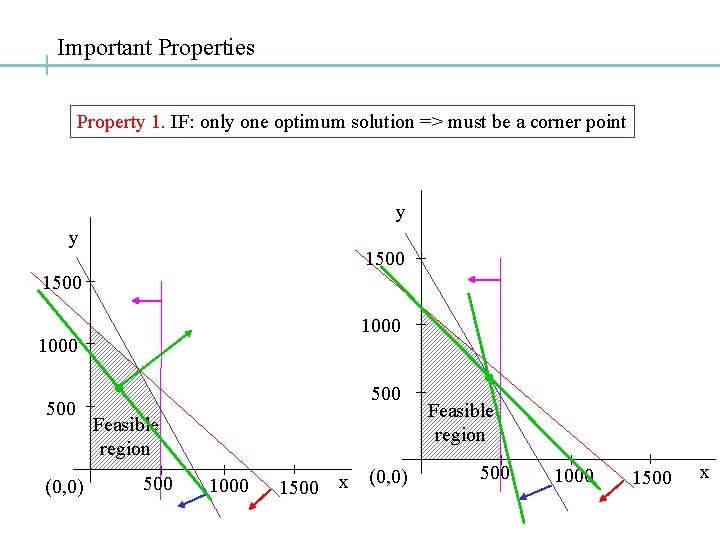
Important Properties Property 1. IF: only one optimum solution => must be a corner point y y 1500 1000 500 (0, 0) 500 Feasible region 500 1000 1500 x (0, 0) Feasible region 500 1000 1500 x

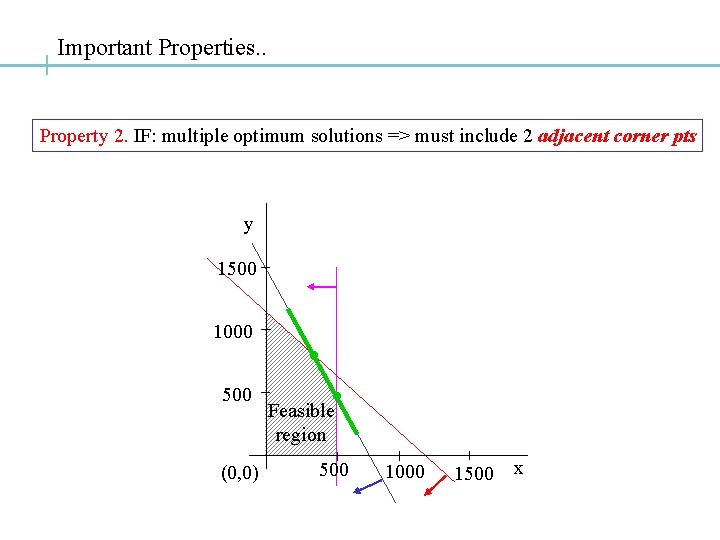
Important Properties. . Property 2. IF: multiple optimum solutions => must include 2 adjacent corner pts y 1500 1000 500 (0, 0) Feasible region 500 1000 1500 x

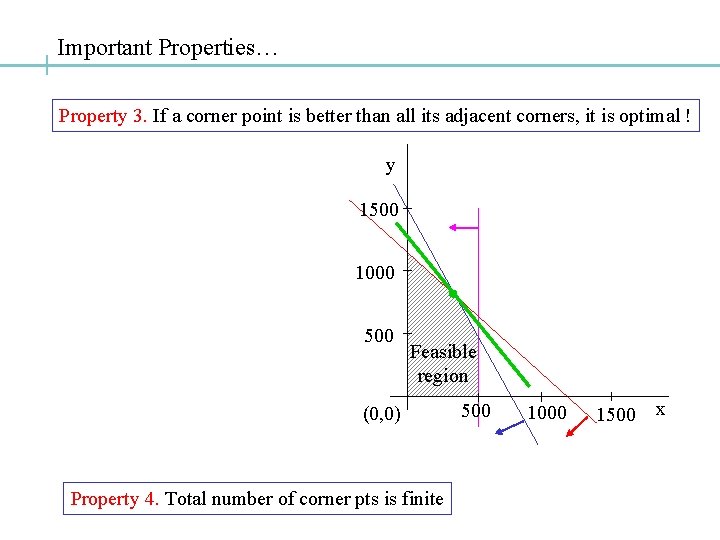
Important Properties… Property 3. If a corner point is better than all its adjacent corners, it is optimal ! y 1500 1000 500 Feasible region (0, 0) Property 4. Total number of corner pts is finite 500 1000 1500 x

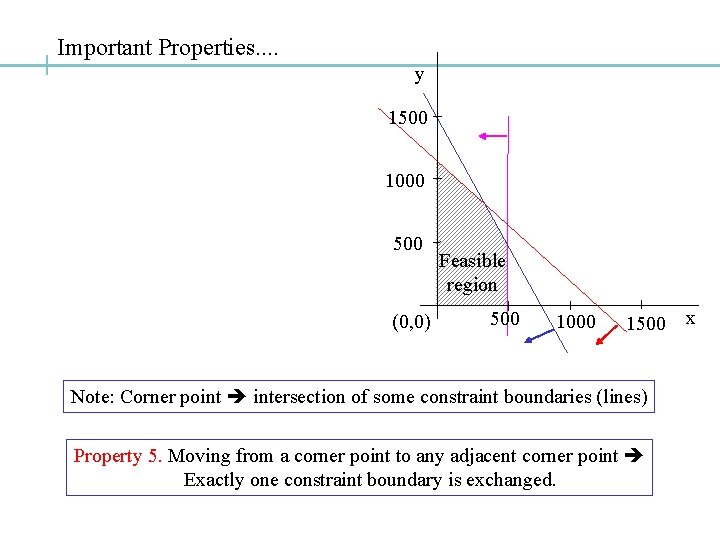
Important Properties. . y 1500 1000 500 (0, 0) Feasible region 500 1000 1500 x Note: Corner point intersection of some constraint boundaries (lines) Property 5. Moving from a corner point to any adjacent corner point Exactly one constraint boundary is exchanged.

The algebra of Simplex Good news We only need to search for the best feasible corner point Bad news A problem with 50 variables, 100 constraints => => ~ 1029 corner points Good news We can use property 5 to guide our searching 100 ! 50 ! (100 -50) !

The outline of Simplex 1. Start at a corner point feasible solution 2. If (there is a better adjacent corner feasible point) then go to one such adjacent corner point; repeat Step 2; else (report this point as the optimum point). Why does this method work ? 1. Constant improvement (=> no cycling) 2. Finite number of corners

The Algebra of Simplex: Gauss elimination Solving for corner points solving a set of simultaneous equations Method: Gaussian elimination Example: x+y=2 x – 2 y = 1 [1] [2] Solve by: 2 x[1] + [2]: [1] - 1 x[2]: 3 x = 5 3 y = 1 => x = 5/3 => y = 1/3

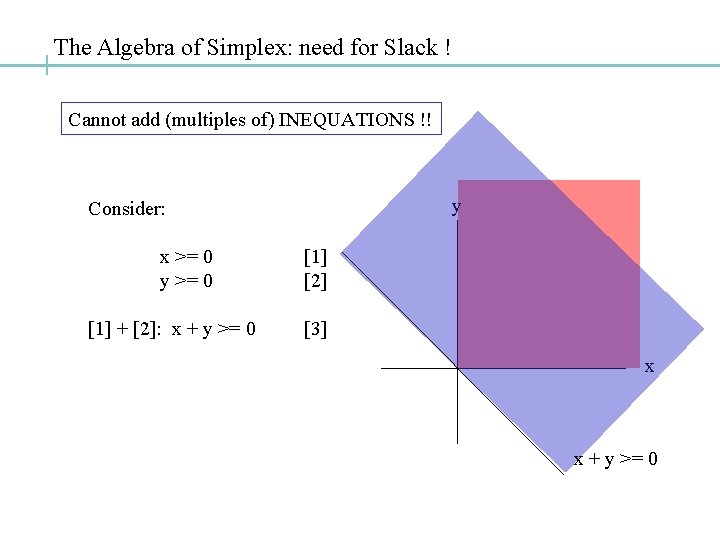
The Algebra of Simplex: need for Slack ! Cannot add (multiples of) INEQUATIONS !! y Consider: x >= 0 y >= 0 [1] + [2]: x + y >= 0 [1] [2] [3] x x + y >= 0

The Algebra of Simplex: Slack To allow us to use Gaussian elimination, Convert the inequalities to equations by using SLACK Variables Inequality 2 x + y ≤ 1500, x, y ≥ 0 x + y ≥ 200 x, y ≥ 0 Equality, with slack variable 2 x + y + s = 1500, x, y, s ≥ 0 x + y – s = 200, x, y, s ≥ 0.

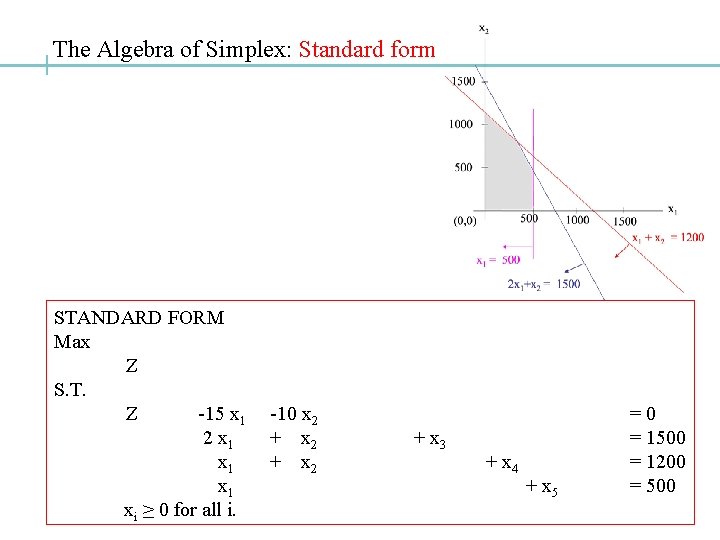
The Algebra of Simplex. . Conversion of the Product mix problem ORIGINAL (almost) STANDARD FORM Maximize z( x, y) = 15 x + 10 y Maximize Z = 15 x 1 + 10 x 2 subject to 2 x + y ≤ 1500 x + y ≤ 1200 x ≤ 500 x ≥ 0, y≥ 0 2 x 1 x 1 + x 2 xi ≥ 0 for all i. + x 3 + x 4 + x 5 = 1500 = 1200 = 500

The Algebra of Simplex… ORIGINAL (almost) STANDARD FORM Maximize z( x, y) = 15 x + 10 y Maximize Z = 15 x 1 + 10 x 2 subject to 2 x + y ≤ 1500 x + y ≤ 1200 x ≤ 500 x ≥ 0, y≥ 0 2 x 1 x 1 + x 2 + x 3 + x 4 xi ≥ 0 for all i. Original problem: n variables, m constraints Standard form: (m+n) variables, m constraints + x 5 = 1500 = 1200 = 500

The Algebra of Simplex… Original problem: n variables, m constraints Standard form: (m+n) variables, m constraints How to use Gaussian elimination ? ? Force some variables = 0 How many to be forced to be 0 ?

Definitions: augmented solution Max Z = 15 x 1 + 10 x 2 S. T. 2 x 1 + x 2 x 1 xi ≥ 0 for all i. Solution: (x 1 x 2) = (200, 200) + x 3 + x 4 + x 5 Augmented solution (200, 900, 800, 300) = 1500 = 1200 = 500

Definitions: BS, BFS Max Z = 15 x 1 + 10 x 2 S. T. 2 x 1 + x 2 x 1 xi ≥ 0 for all i. + x 3 + x 4 + x 5 = 1500 = 1200 = 500 Basic solution Augmented, corner-point solution Examples basic infeasible solution : ( 500, 700, -200, 0, 0) basic feasible solution: (500, 0, 500, 700, 0)

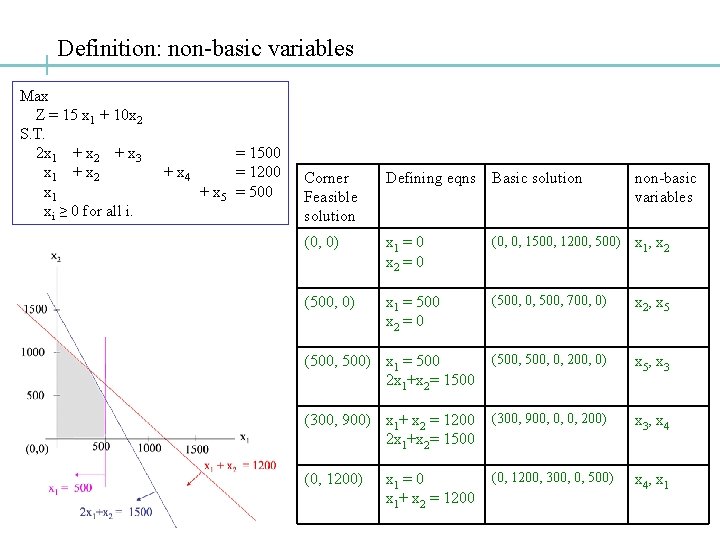
Definition: non-basic variables Max Z = 15 x 1 + 10 x 2 S. T. 2 x 1 + x 2 + x 3 x 1 + x 2 x 1 xi ≥ 0 for all i. = 1500 + x 4 = 1200 + x 5 = 500 Corner Feasible solution Defining eqns Basic solution non-basic variables (0, 0) x 1 = 0 x 2 = 0 (0, 0, 1500, 1200, 500) x 1, x 2 (500, 0) x 1 = 500 x 2 = 0 (500, 0, 500, 700, 0) x 2, x 5 (500, 500) x 1 = 500 2 x 1+x 2= 1500 (500, 0, 200, 0) x 5, x 3 (300, 900) x 1+ x 2 = 1200 2 x 1+x 2= 1500 (300, 900, 0, 0, 200) x 3, x 4 (0, 1200) (0, 1200, 300, 0, 500) x 4, x 1 = 0 x 1+ x 2 = 1200

The Algebra of Simplex Max Z = 15 x 1 + 10 x 2 S. T. 2 x 1 + x 2 + x 3 x 1 + x 2 x 1 xi ≥ 0 for all i. = 1500 + x 4 = 1200 + x 5 = 500 Corner infeasible solution Defining eqns Basic infeasible solution non-basic variables (750, 0) x 2 = 0 2 x 1+ x 2 = 1500 (750, 0, 0, 450, -250) x 2, x 3 (1200, 0) x 2 = 0 x 1 + x 2 = 1200 (1200, 0, -900, 0, -700) x 2, x 4 (500, 700) x 1 + x 2 = 1200 x 1 = 500 (500, 700, -200, 0, 0) x 4, x 5 (0, 1500) (0, 1500, 0, -300, 500) x 1, x 3 x 1 = 0 2 x 1+ x 2 = 1500

The Algebra of Simplex: Standard form STANDARD FORM Max Z S. T. Z -15 x 1 2 x 1 x 1 xi ≥ 0 for all i. -10 x 2 + x 3 + x 4 + x 5 =0 = 1500 = 1200 = 500

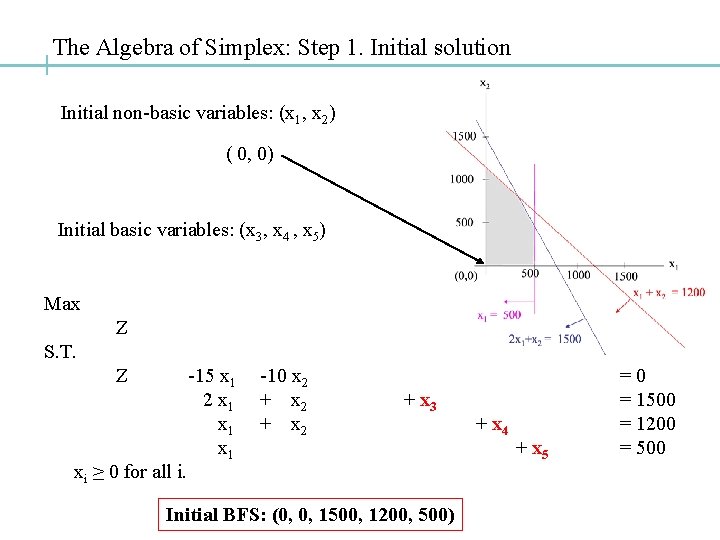
The Algebra of Simplex: Step 1. Initial solution Initial non-basic variables: (x 1, x 2) ( 0, 0) Initial basic variables: (x 3, x 4 , x 5) Max Z S. T. Z xi ≥ 0 for all i. -15 x 1 2 x 1 x 1 -10 x 2 + x 3 Initial BFS: (0, 0, 1500, 1200, 500) + x 4 + x 5 =0 = 1500 = 1200 = 500

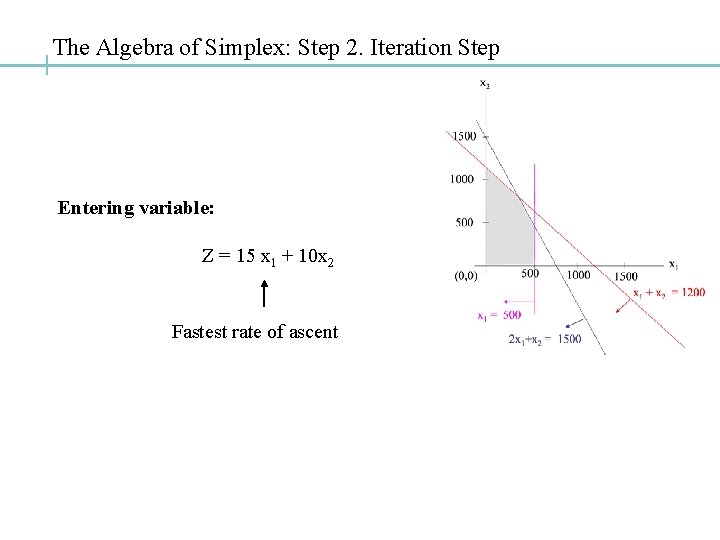
The Algebra of Simplex: Step 2. Iteration Step Entering variable: Z = 15 x 1 + 10 x 2 Fastest rate of ascent

The Algebra of Simplex: Step 2. Iteration Step Max S. T. Entering Z Z xi ≥ 0 for all i. -15 x 1 2 x 1 x 1 - 10 x 2 + x 3 + x 4 + x 5 Leaving variable Consider first constraint: 2 x 1 + x 2 + x 3 = 1500 - 2 x 1 - x 2 Bound on x 1: 1500/2 = 750 =0 = 1500 = 1200 = 500

The Algebra of Simplex: Step 2. Iteration Step Leaving variable Max S. T. Z Z xi ≥ 0 for all i. -15 x 1 2 x 1 x 1 - 10 x 2 + x 3 + x 4 + x 5 =0 = 1500 = 1200 = 500

The Algebra of Simplex: Step 2. Iteration Step Enter: x 1 Z -15 x 1 Leave: x 5 -10 x 2 2 x 1 + x 2 + x 3 + x 4 x 1 + x 5 =0 [0 -0] + 15 x [0 -3] = 1500 [0 -1] - 2 x [0 -3] = 1200 [0 -2] - [0 -3] = 500 [0 -3] ROW OPERATIONS so that Each row has exactly one basic variable The coefficient of each basic variable = +1

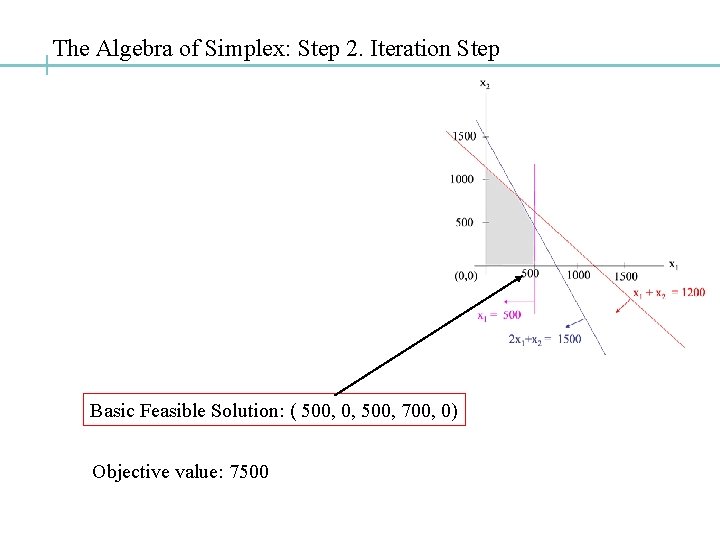
The Algebra of Simplex: Step 2. Iteration Step Z -15 x 1 -10 x 2 2 x 1 + x 2 + x 3 + x 4 x 1 + x 5 =0 [0 -0] = 1500 [0 -1] = 1200 [0 -2] = 500 [0 -3] Row operations Z -10 x 2 x 2 x 1 + x 3 + x 4 +15 x 5 = 7500 [1 -0] - 2 x 5 = 500 [1 -1] - x 5 = 700 [1 -2] + x 5 = 500 [1 -3] Basic Feasible Solution: ( 500, 0, 500, 700, 0)

The Algebra of Simplex: Step 2. Iteration Step Basic Feasible Solution: ( 500, 0, 500, 700, 0) Objective value: 7500

The Algebra of Simplex: Step 3. Stopping condition Stopping Rule: Stop when objective cannot be improved. Z -10 x 2 x 2 x 1 + x 3 + x 4 +15 x 5 = 7500 [1 -0] - 2 x 5 = 500 [1 -1] - x 5 = 700 [1 -2] + x 5 = 500 [1 -3] New entering variable: x 2

The Algebra of Simplex: Second Iteration. . New entering variable: x 2 Z -10 x 2 x 2 x 1 Analysis for leaving variable: + x 3 + x 4 +15 x 5 = 7500 [1 -0] - 2 x 5 = 500 [1 -1] - x 5 = 700 [1 -2] + x 5 = 500 [1 -3]

The Algebra of Simplex: Step 2. Iteration Step Enter: x 2 Z Leave: x 3 -10 x 2 + x 3 x 2 x 1 + x 4 +15 x 5 = 7500 [1 -0] - 2 x 5 = 500 [1 -1] - x 5 = 700 [1 -2] + x 5 = 500 [1 -3] ROW OPERATIONS so that Each row has exactly one basic variable The coefficient of each basic variable = +1 + 10 x [1 -1] - [1 -1]

The Algebra of Simplex: Step 2. Iteration Step After row operations: Z x 2 +10 x 3 -5 x 5 = 12, 500 [2 -0] + x 3 - 2 x 5 = 500 [2 -1] + x 5 = 200 [2 -2] + x 5 = 500 [2 -3] - x 3 + x 4 x 1 Basic Feasible Solution: ( 500, 0, 200, 0) Have we found the OPTIMUM ?

The Algebra of Simplex: Third Iteration New entering variable: x 5 Z x 2 +10 x 3 -5 x 5 = 12, 500 [2 -0] + x 3 - 2 x 5 = 500 [2 -1] + x 5 = 200 [2 -2] + x 5 = 500 [2 -3] - x 3 + x 4 x 1 Analysis for leaving variable: Basic variable Equation Upper bound for x 5 x 2 = 500 + 2 x 5 - x 3 no limit on x 5 x 4 = 200 + x 3 - x 5 ≤ 200 x 1 = 500 – x 5 ≤ 500 minimum

The Algebra of Simplex: Step 2. Third iteration. . Enter: x 5 Leave: x 4 Z x 2 +10 x 3 -5 x 5 = 12, 500 [2 -0] + 5 x [2 -2] + x 3 - 2 x 5 = 500 [2 -1] + 2 x [2 -2] + x 5 = 200 [2 -2] + x 5 = 500 [2 -3] - x 3 x 1 + x 4 ROW OPERATIONS so that Each row has exactly one basic variable The coefficient of each basic variable = +1 - [2 -2]

The Algebra of Simplex: Step 2. Iteration Step After row operations: Z x 2 x 1 +5 x 3 + 5 x 4 = 13, 500 [3 -0] - x 3 + 2 x 4 = 900 [3 -1] - x 3 + x 4 = 200 [3 -2] + x 3 - x 4 = 300 [3 -3] + x 5 Basic Feasible Solution: ( 300, 900, 0, 0, 200) Have we found the OPTIMUM ?

The Algebra of Simplex: Some important points 1. Higher dimensions Each step: ONE entering variable ONE leaving variable Each constraint equation has same format as our example 2. Many candidates for entering variable e. g. Z = 200 + 10 x 1 + x 2 + 10 x 3 Just pick any one

The Algebra of Simplex: Some important points. . 3. Many candidates for leaving variable Degenerate case, rare. 4. No candidate for leaving variable Unbounded objective !? 5. Minimization problems Minimize Z == Maximize -Z next topic: inventory control