LINEAR PROGRAMMING Example 1 Maximise I x 0

  • Slides: 27
Download presentation
LINEAR PROGRAMMING Example 1 Maximise I = x + 0. 8 y subject to

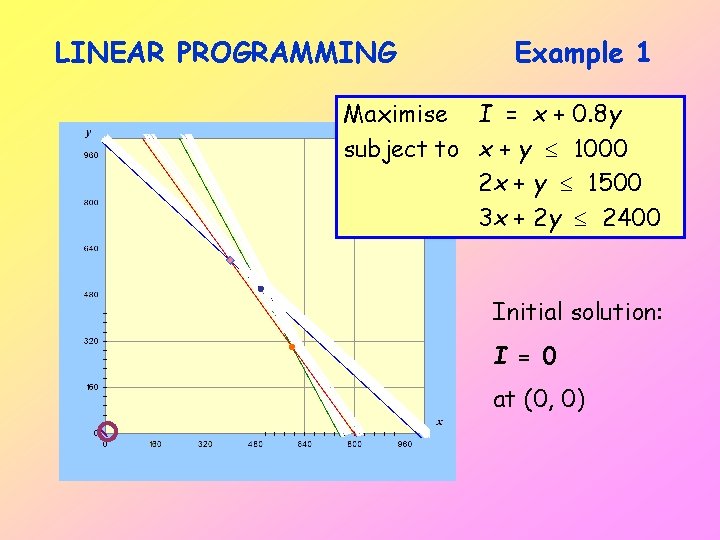
LINEAR PROGRAMMING Example 1 Maximise I = x + 0. 8 y subject to x + y 1000 2 x + y 1500 3 x + 2 y 2400 Initial solution: I = 0 at (0, 0)

LINEAR PROGRAMMING Maximise subject to Maximise where subject to Example 1 I = x

LINEAR PROGRAMMING Maximise subject to Maximise where subject to Example 1 I = x + 0. 8 y x + y 1000 2 x + y 1500 3 x + 2 y 2400 I I - x - 0. 8 y x + y + s 1 2 x + y + s 2 3 x + 2 y + s 3 = 0 = 1000 = 1500 = 2400

SIMPLEX TABLEAU Initial solution I x y s 1 s 2 s 3 RHS

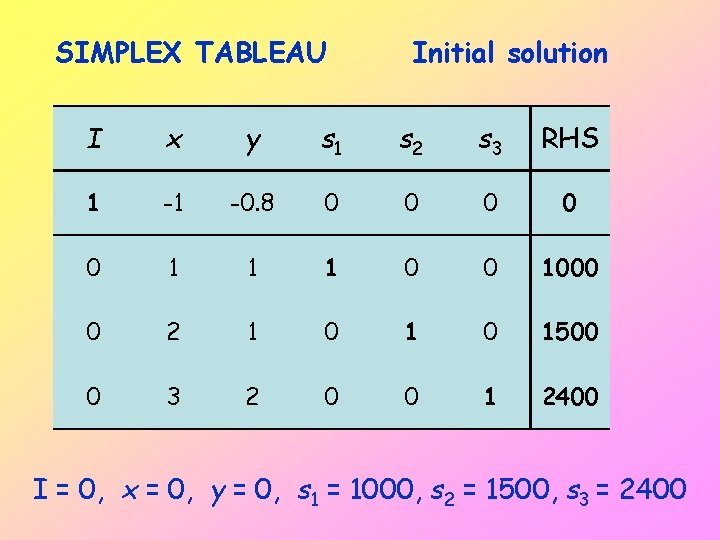
SIMPLEX TABLEAU Initial solution I x y s 1 s 2 s 3 RHS 1 -1 -0. 8 0 0 0 1 1 1 0 0 1000 0 2 1 0 1500 0 3 2 0 0 1 2400 I = 0, x = 0, y = 0, s 1 = 1000, s 2 = 1500, s 3 = 2400

PIVOT 1 Choosing the pivot column I x y s 1 s 2 s

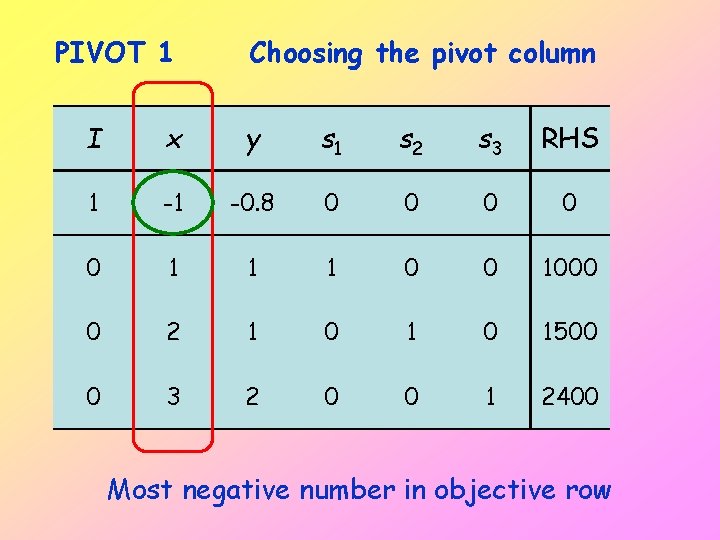
PIVOT 1 Choosing the pivot column I x y s 1 s 2 s 3 RHS 1 -1 -0. 8 0 0 0 1 1 1 0 0 1000 0 2 1 0 1500 0 3 2 0 0 1 2400 Most negative number in objective row

PIVOT 1 Choosing the pivot element I x y s 1 s 2 s

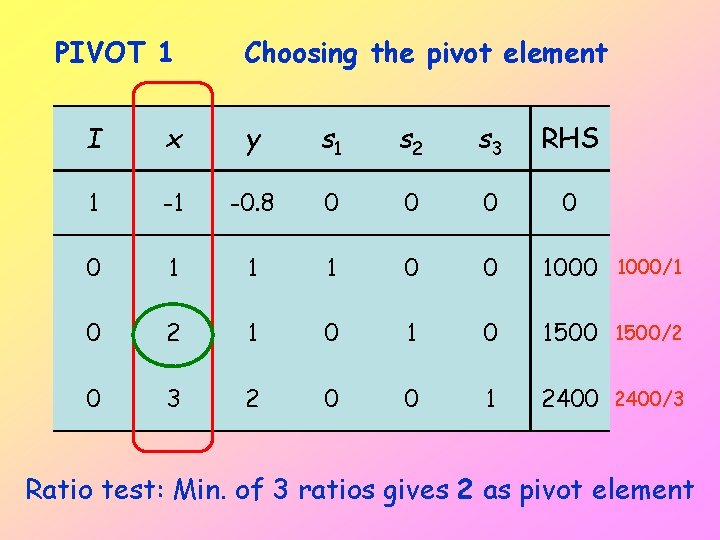
PIVOT 1 Choosing the pivot element I x y s 1 s 2 s 3 RHS 1 -1 -0. 8 0 0 0 1 1 1 0 0 1000/1 0 2 1 0 1500/2 0 3 2 0 0 1 2400/3 Ratio test: Min. of 3 ratios gives 2 as pivot element

PIVOT 1 Making the pivot I x y s 1 s 2 s 3

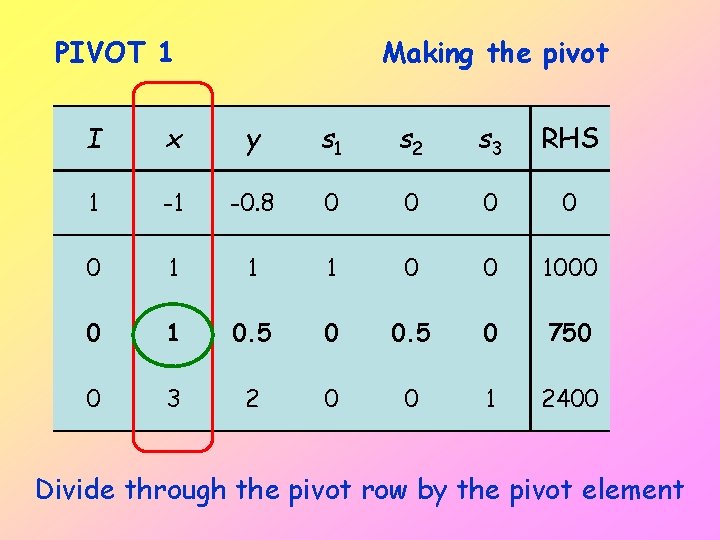
PIVOT 1 Making the pivot I x y s 1 s 2 s 3 RHS 1 -1 -0. 8 0 0 0 1 1 1 0 0 1000 0 1 0. 5 0 750 0 3 2 0 0 1 2400 Divide through the pivot row by the pivot element

PIVOT 1 Making the pivot I x y s 1 s 2 s 3

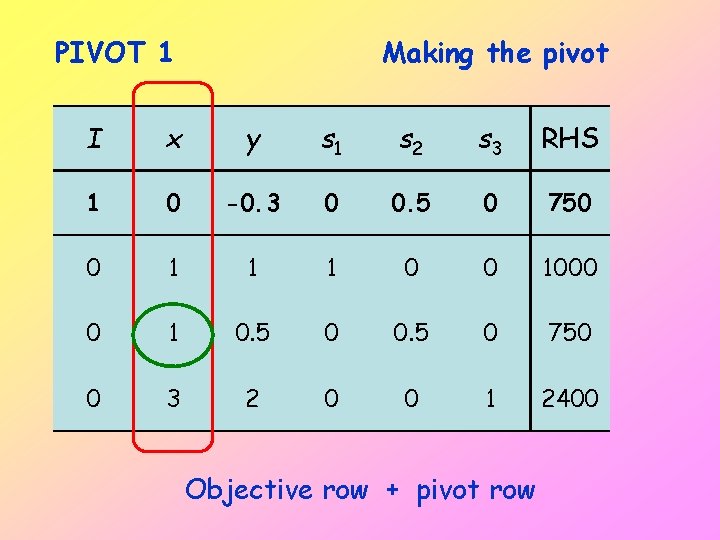
PIVOT 1 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 -0. 3 0 0. 5 0 750 0 1 1 1 0 0 1000 0 1 0. 5 0 750 0 3 2 0 0 1 2400 Objective row + pivot row

PIVOT 1 Making the pivot I x y s 1 s 2 s 3

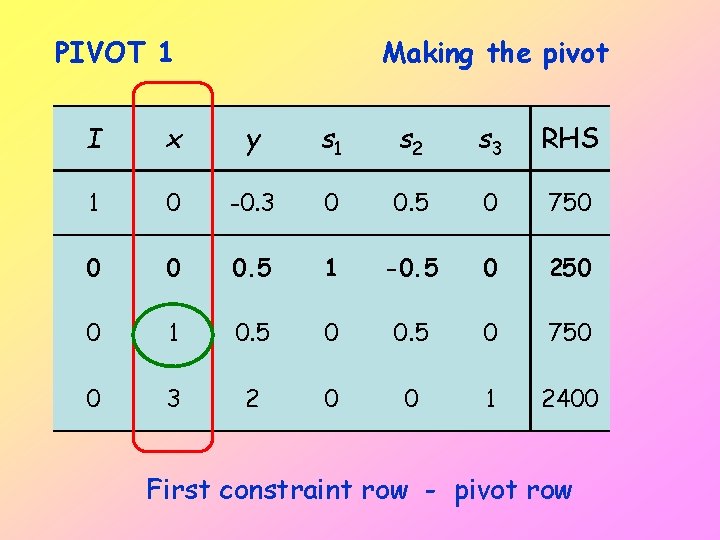
PIVOT 1 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 -0. 3 0 0. 5 0 750 0 0 0. 5 1 -0. 5 0 250 0 1 0. 5 0 750 0 3 2 0 0 1 2400 First constraint row - pivot row

PIVOT 1 Making the pivot I x y s 1 s 2 s 3

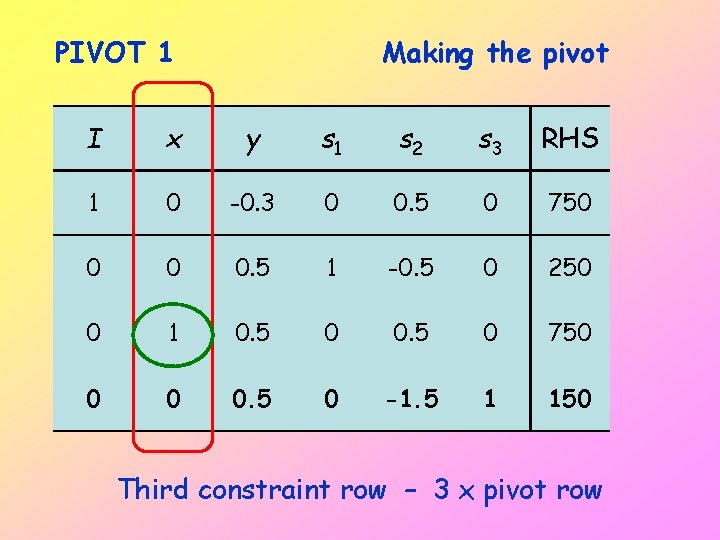
PIVOT 1 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 -0. 3 0 0. 5 0 750 0 0 0. 5 1 -0. 5 0 250 0 1 0. 5 0 750 0 0 0. 5 0 -1. 5 1 150 Third constraint row – 3 x pivot row

PIVOT 1 New solution I x y s 1 s 2 s 3 RHS

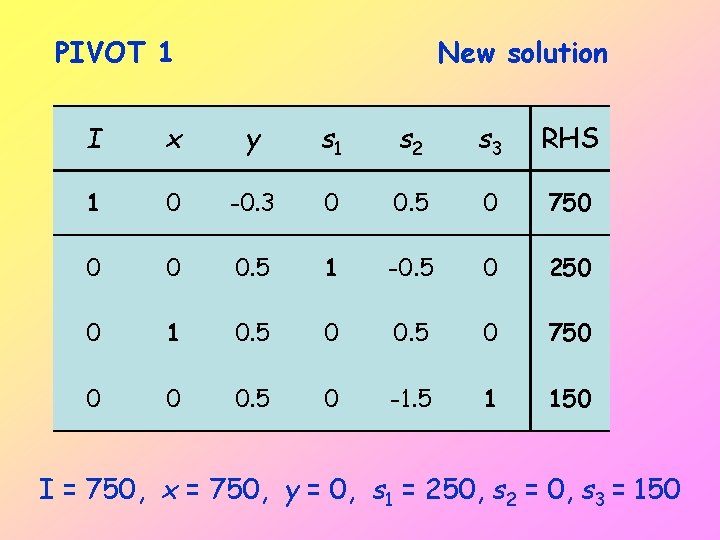
PIVOT 1 New solution I x y s 1 s 2 s 3 RHS 1 0 -0. 3 0 0. 5 0 750 0 0 0. 5 1 -0. 5 0 250 0 1 0. 5 0 750 0 0 0. 5 0 -1. 5 1 150 I = 750, x = 750, y = 0, s 1 = 250, s 2 = 0, s 3 = 150

LINEAR PROGRAMMING Example Maximise I = x + 0. 8 y subject to x

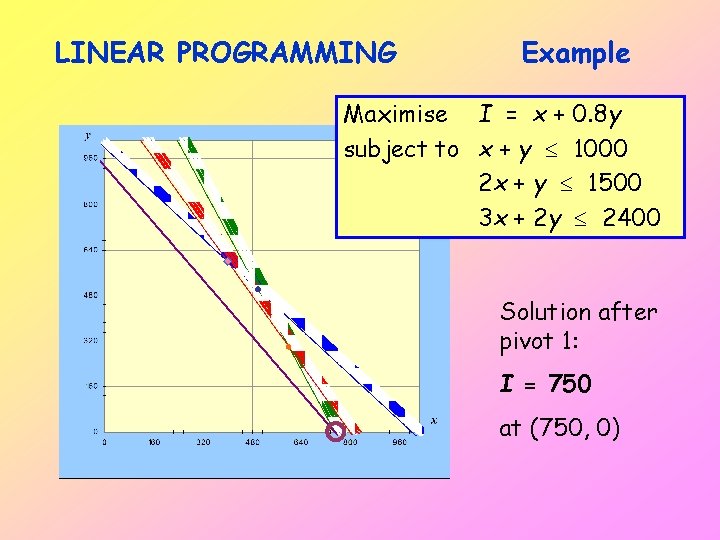
LINEAR PROGRAMMING Example Maximise I = x + 0. 8 y subject to x + y 1000 2 x + y 1500 3 x + 2 y 2400 Solution after pivot 1: I = 750 at (750, 0)

PIVOT 2 Choosing the pivot column I x y s 1 s 2 s

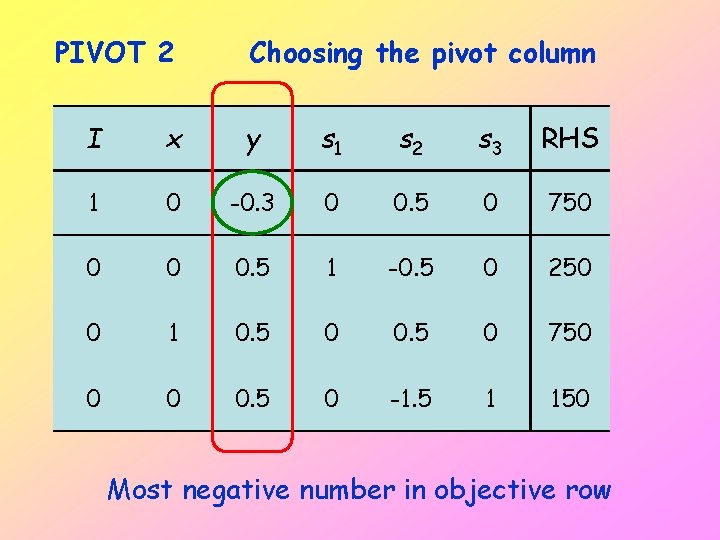
PIVOT 2 Choosing the pivot column I x y s 1 s 2 s 3 RHS 1 0 -0. 3 0 0. 5 0 750 0 0 0. 5 1 -0. 5 0 250 0 1 0. 5 0 750 0 0 0. 5 0 -1. 5 1 150 Most negative number in objective row

PIVOT 2 Choosing the pivot element I x y s 1 s 2 s

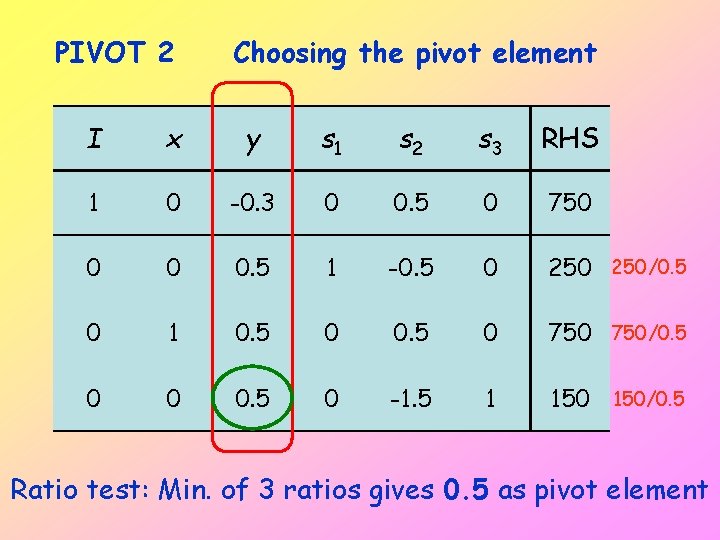
PIVOT 2 Choosing the pivot element I x y s 1 s 2 s 3 RHS 1 0 -0. 3 0 0. 5 0 750 0 0 0. 5 1 -0. 5 0 250/0. 5 0 1 0. 5 0 750/0. 5 0 0 0. 5 0 -1. 5 1 150/0. 5 Ratio test: Min. of 3 ratios gives 0. 5 as pivot element

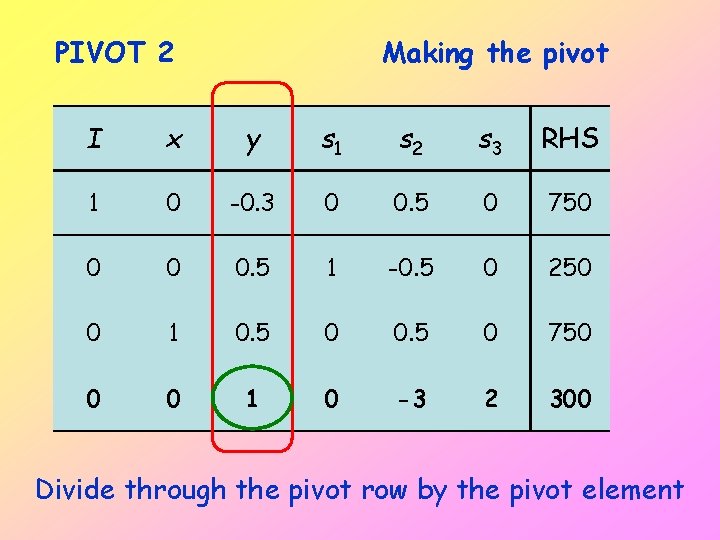
PIVOT 2 Making the pivot I x y s 1 s 2 s 3

PIVOT 2 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 -0. 3 0 0. 5 0 750 0 0 0. 5 1 -0. 5 0 250 0 1 0. 5 0 750 0 0 1 0 -3 2 300 Divide through the pivot row by the pivot element

PIVOT 2 Making the pivot I x y s 1 s 2 s 3

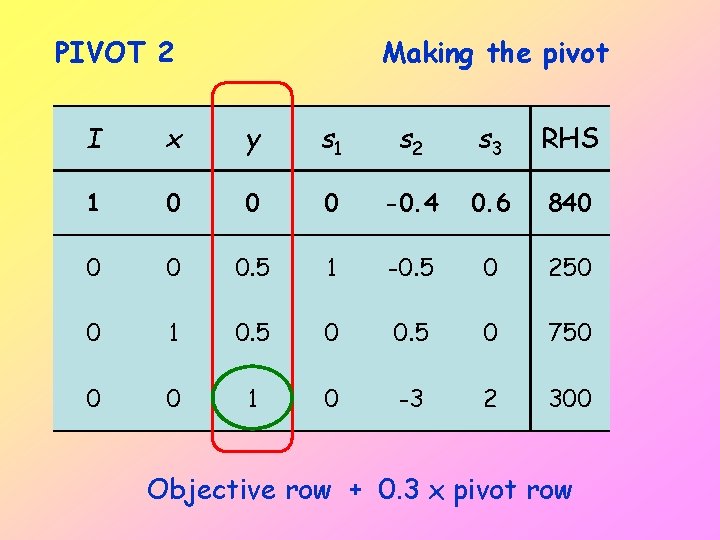
PIVOT 2 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 0 0 -0. 4 0. 6 840 0 0 0. 5 1 -0. 5 0 250 0 1 0. 5 0 750 0 0 1 0 -3 2 300 Objective row + 0. 3 x pivot row

PIVOT 2 Making the pivot I x y s 1 s 2 s 3

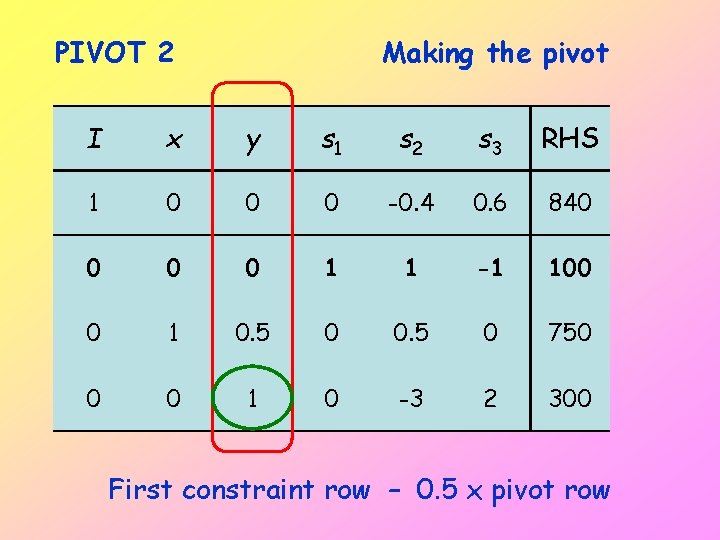
PIVOT 2 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 0 0 -0. 4 0. 6 840 0 1 1 -1 100 0 1 0. 5 0 750 0 0 1 0 -3 2 300 First constraint row – 0. 5 x pivot row

PIVOT 2 Making the pivot I x y s 1 s 2 s 3

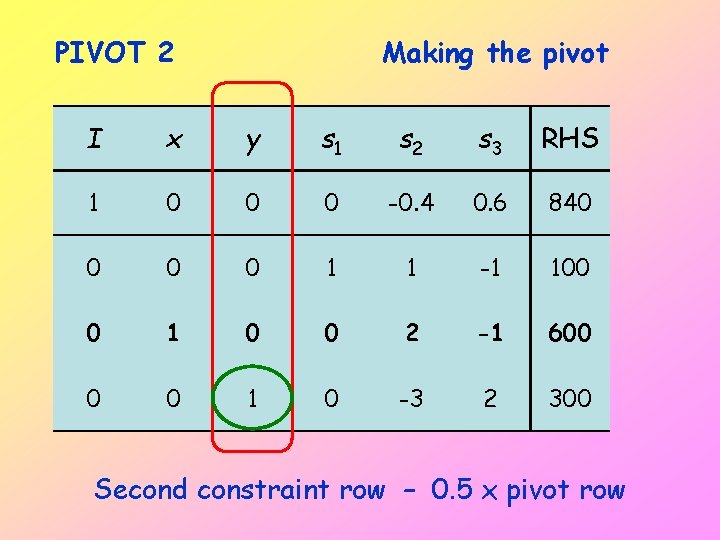
PIVOT 2 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 0 0 -0. 4 0. 6 840 0 1 1 -1 100 0 1 0 0 2 -1 600 0 0 1 0 -3 2 300 Second constraint row – 0. 5 x pivot row

PIVOT 2 New solution I x y s 1 s 2 s 3 RHS

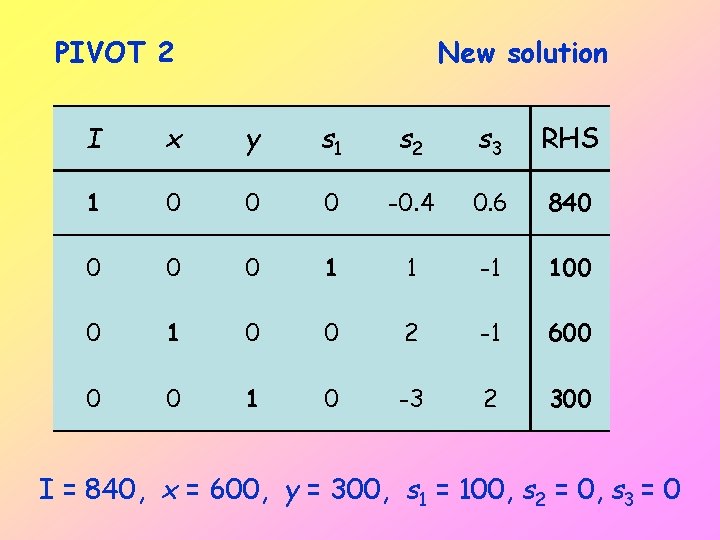
PIVOT 2 New solution I x y s 1 s 2 s 3 RHS 1 0 0 0 -0. 4 0. 6 840 0 1 1 -1 100 0 1 0 0 2 -1 600 0 0 1 0 -3 2 300 I = 840, x = 600, y = 300, s 1 = 100, s 2 = 0, s 3 = 0

LINEAR PROGRAMMING Example Maximise I = x + 0. 8 y subject to x

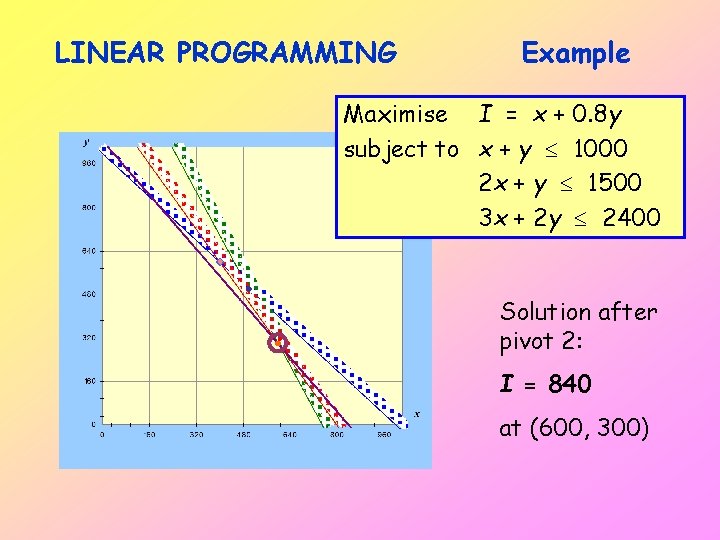
LINEAR PROGRAMMING Example Maximise I = x + 0. 8 y subject to x + y 1000 2 x + y 1500 3 x + 2 y 2400 Solution after pivot 2: I = 840 at (600, 300)

PIVOT 3 Choosing the pivot column I x y s 1 s 2 s

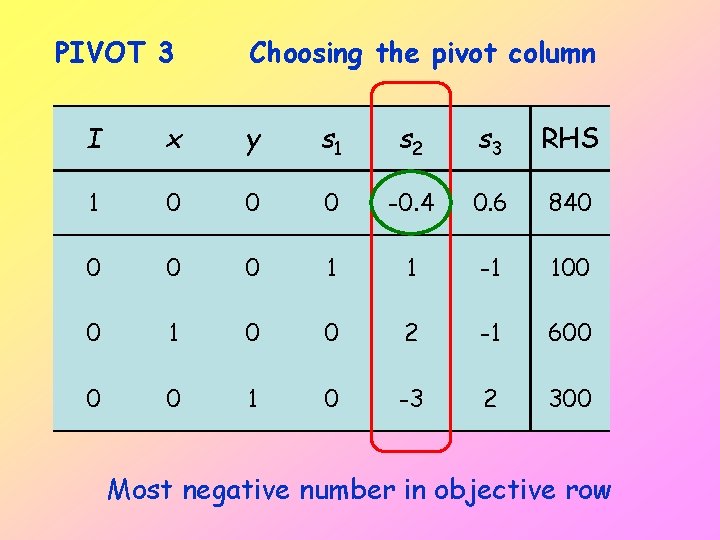
PIVOT 3 Choosing the pivot column I x y s 1 s 2 s 3 RHS 1 0 0 0 -0. 4 0. 6 840 0 1 1 -1 100 0 1 0 0 2 -1 600 0 0 1 0 -3 2 300 Most negative number in objective row

PIVOT 3 Choosing the pivot element I x y s 1 s 2 s

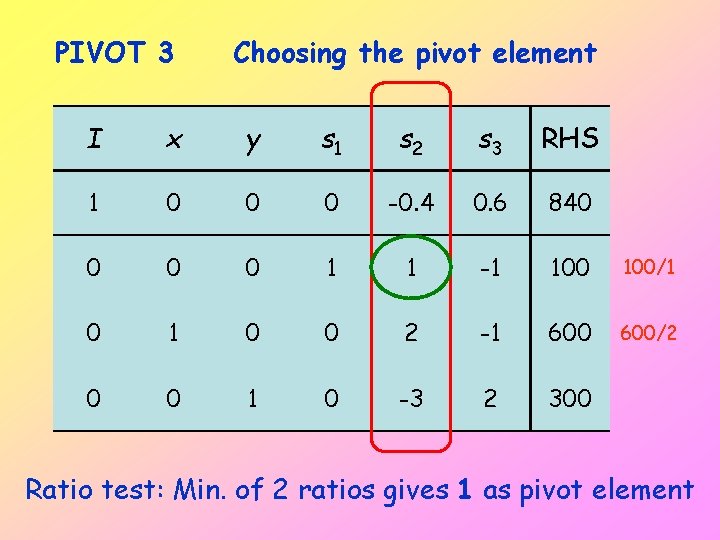
PIVOT 3 Choosing the pivot element I x y s 1 s 2 s 3 RHS 1 0 0 0 -0. 4 0. 6 840 0 1 1 -1 100/1 0 0 2 -1 600/2 0 0 1 0 -3 2 300 Ratio test: Min. of 2 ratios gives 1 as pivot element

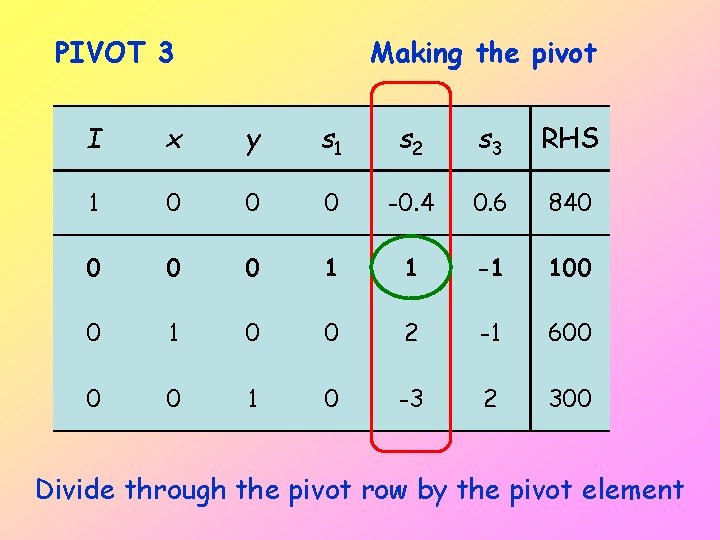
PIVOT 3 Making the pivot I x y s 1 s 2 s 3

PIVOT 3 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 0 0 -0. 4 0. 6 840 0 1 1 -1 100 0 1 0 0 2 -1 600 0 0 1 0 -3 2 300 Divide through the pivot row by the pivot element

PIVOT 3 Making the pivot I x y s 1 s 2 s 3

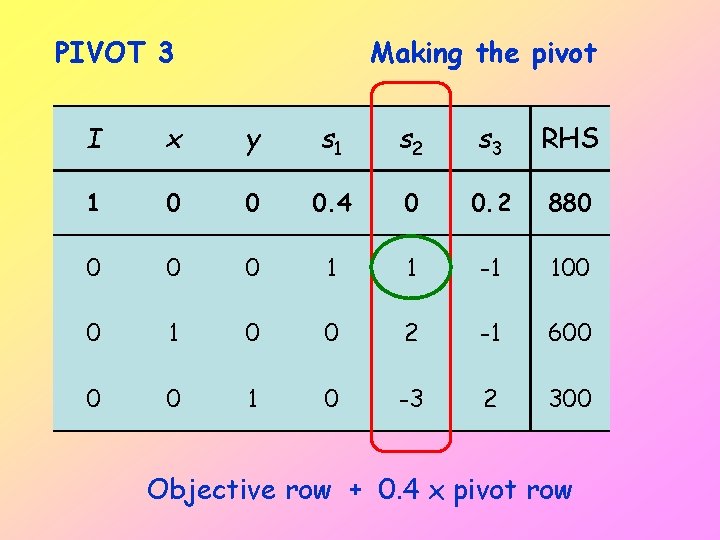
PIVOT 3 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 0 0. 4 0 0. 2 880 0 1 1 -1 100 0 1 0 0 2 -1 600 0 0 1 0 -3 2 300 Objective row + 0. 4 x pivot row

PIVOT 3 Making the pivot I x y s 1 s 2 s 3

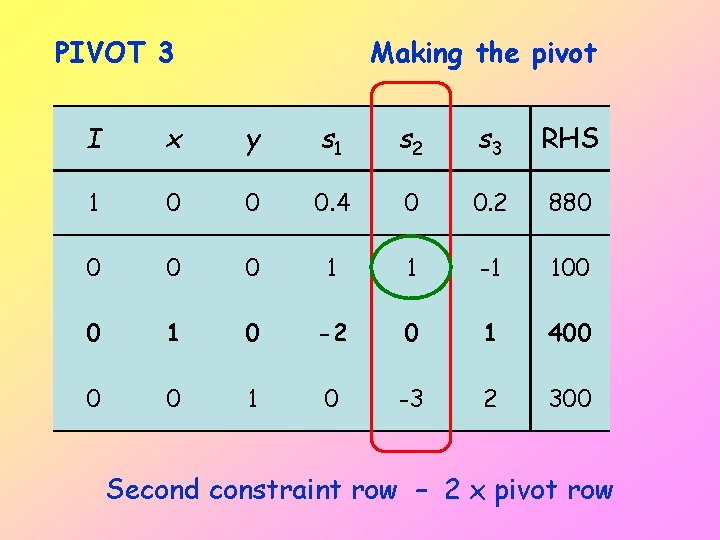
PIVOT 3 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 0 0. 4 0 0. 2 880 0 1 1 -1 100 0 1 0 -2 0 1 400 0 0 1 0 -3 2 300 Second constraint row – 2 x pivot row

PIVOT 3 Making the pivot I x y s 1 s 2 s 3

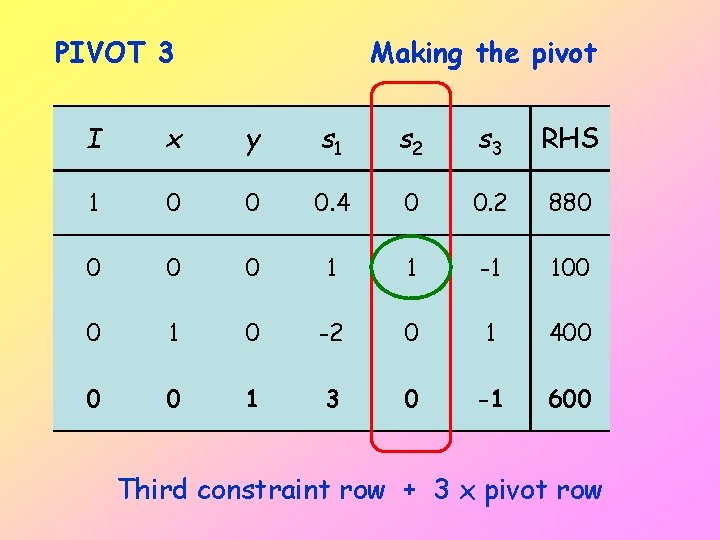
PIVOT 3 Making the pivot I x y s 1 s 2 s 3 RHS 1 0 0 0. 4 0 0. 2 880 0 1 1 -1 100 0 1 0 -2 0 1 400 0 0 1 3 0 -1 600 Third constraint row + 3 x pivot row

PIVOT 3 Optimal solution I x y s 1 s 2 s 3 RHS

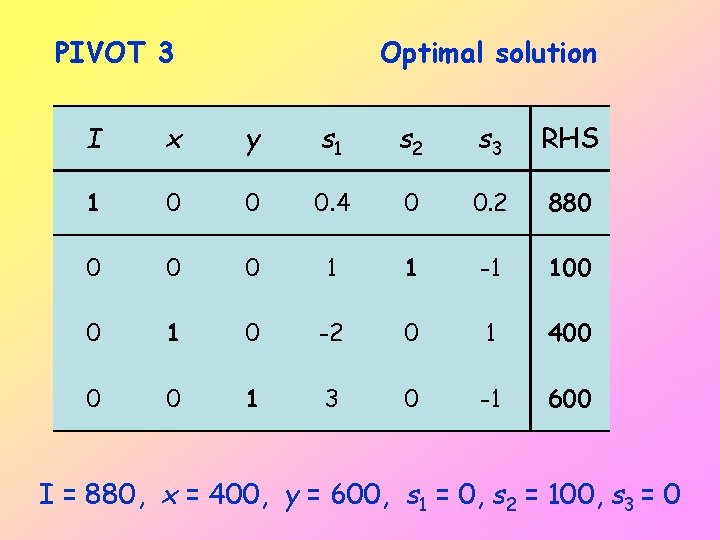
PIVOT 3 Optimal solution I x y s 1 s 2 s 3 RHS 1 0 0 0. 4 0 0. 2 880 0 1 1 -1 100 0 1 0 -2 0 1 400 0 0 1 3 0 -1 600 I = 880, x = 400, y = 600, s 1 = 0, s 2 = 100, s 3 = 0

LINEAR PROGRAMMING Example Maximise I = x + 0. 8 y subject to x

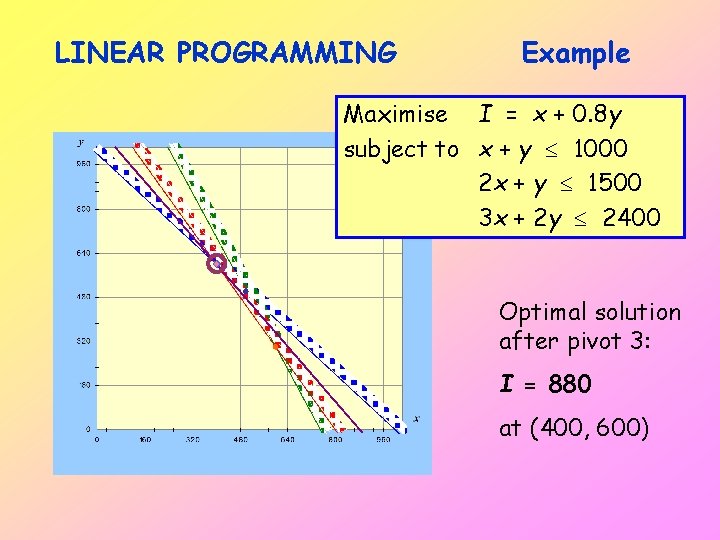
LINEAR PROGRAMMING Example Maximise I = x + 0. 8 y subject to x + y 1000 2 x + y 1500 3 x + 2 y 2400 Optimal solution after pivot 3: I = 880 at (400, 600)