Linear programming Applications Jennys Bakery makes two types

Linear programming Applications

�Jenny’s Bakery makes two types of birthday cakes: yellow cake, which sells for $25, and strawberry cake, which sells for $35. Both cakes are the same size but the decorating and assembly time required for the yellow cake is 2 hours while the time is 3 hours for the strawberry cake. There are 450 hours of labor available for production. How many of each type of cake should be made to maximize revenue? Story problem 1

�Let x = the number of yellow cakes y = the number of strawberry cakes R(x, y) = the revenue generated by sales �NOTE: Choose variables that help you to remember. Some of you may want to use y for the number of yellow cakes and s for the number of strawberry cakes. Remember to label your axes correctly. Define the variables.

1. Since she can’t have “negative” numbers of cakes, the graph must be in Quadrant So the first 2 constraints are What are the constraints?

2. Since the only other constraint given in the problem is a time constraint, she needs to consider how much time each cake takes to bake and decorate and how much total time is needed for labor. It takes 2 hours to bake and decorate the yellow cake. It takes 3 hours to bake and decorate the strawberry cake. There are no more than 450 hours of labor available. What are the constraints?

�What are she trying to do? (maximize revenue – of course) �We need to know how many of each cake to produce to get the most money IN. �The yellow cake sells for $25 each. �The strawberry cake sells for $35 each. What is the objective function?

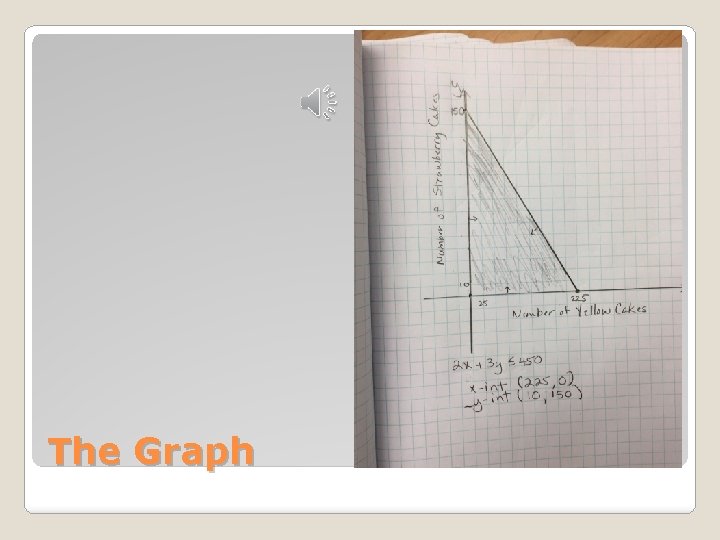
�Remember to set the intervals on the axes to make sense in the problem. �Using the intercept method works well in this problem. Graph the feasible region.

The Graph

Vertices R(x, y) = 25 x + 35 y Value (0, 0) 25(0) + 35(0) $0 (150, 0) 25(150) + 35(0) $3750 (0, 225) 25(0) + 35(225) $7875 Maximum * MAXIMUM The Optimization Law states that if a MINIMUM or MAXIMUM value is possible in an objective function, either WILL occur at the vertex of a polygonal area!!! (Remember: Minimizing COST is optimal – just like maximizing PROFIT is optimal. ) So, Jenny should bake no yellow cakes and 225 strawberry cakes to maximize her profit at $7875. Optimization Law holds!

�The manager of a travel agency is printing brochures and fliers to advertise special discounts on vacation spots during the summer months. Each brochure costs $0. 08 to print, and each flier costs $0. 04 to print. A brochure requires 3 pages, and a flier requires 2 pages. The manager does not want to use more than 600 pages, and she needs at least 50 brochures and 150 fliers. How many of each should she print to minimize the cost? Story Problem 2

�Let x = the number of brochures. �Let y = the number of fliers. Define the variables.

�She needs at least 50 brochures. �She needs at least 150 fliers. �Each brochure uses 3 pages. �Each flier uses 2 pages. �She can use no more than 600 pages. What are the constraints?

�What is she trying to do? She wants to MINIMIZE cost. �Each brochure costs $0. 08. �Each flier costs $0. 04. What is the objective function?

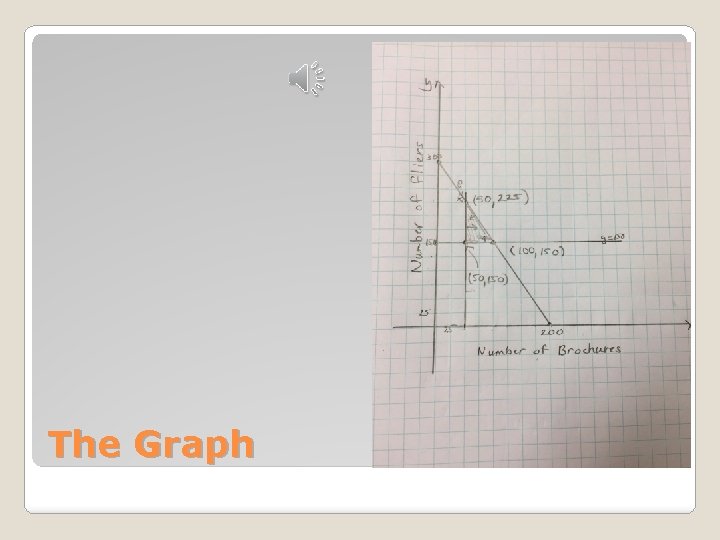
�Remember to set the intervals on the axes to make sense in the problem. �Using the intercept method works well in this problem. Graph the feasible region.

The Graph

Vertices C(x, y) = 0. 08 x + 0. 04 y Value MINIMUM * (50, 150) 0. 08(50) + 0. 04(150) $10 *MINIMUM (50, 225) 0. 08(50) + 0. 04(225) $13 (100, 150) 0. 08(100) + 0. 04(150) $14 The Optimization Law states that if a MINIMUM or MAXIMUM value is possible in an objective function, either WILL occur at the vertex of a polygonal area!!! (Remember: Minimizing COST is optimal – just like maximizing PROFIT is optimal. ) So, the manager should produce 50 brochures and 150 fliers to have a minimum production cost of $10. Optimization Law holds!