Linear Programming and Simplex Algorithm Reference Numerical Recipe








![QSopt [ref] • Contains a GUI and a callable library 11 QSopt [ref] • Contains a GUI and a callable library 11](https://slidetodoc.com/presentation_image_h2/f65db55c44867c93d753e538ba801286/image-11.jpg)



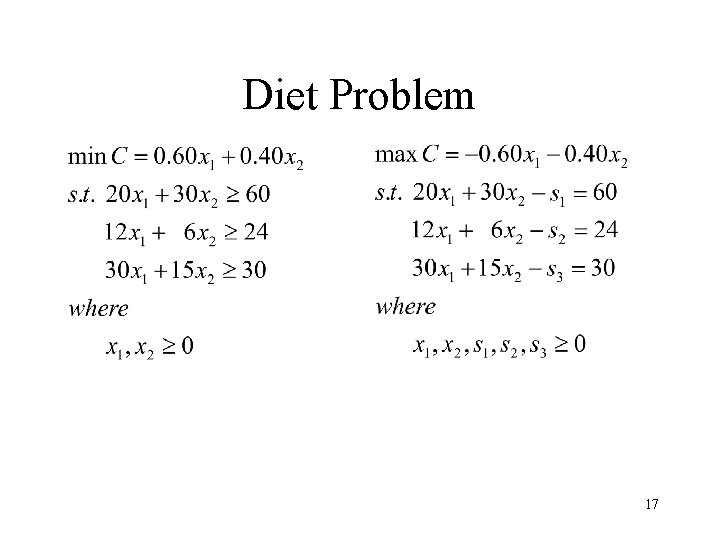



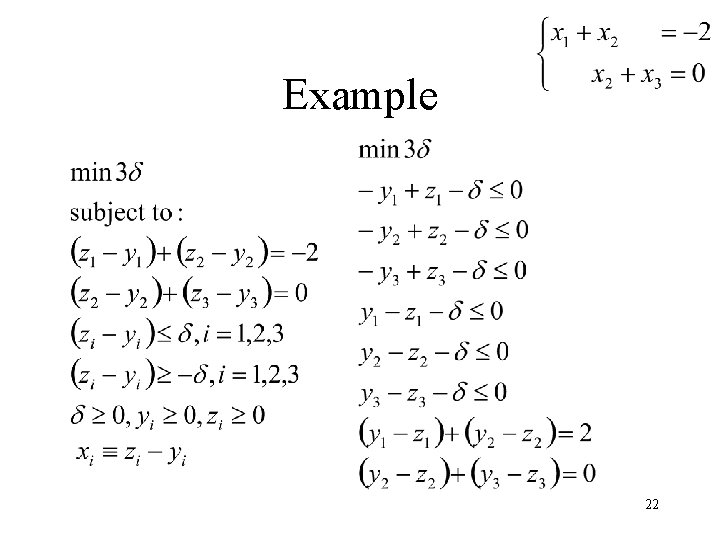









![QSopt [ref] • Contains a GUI and a callable library 35 QSopt [ref] • Contains a GUI and a callable library 35](https://slidetodoc.com/presentation_image_h2/f65db55c44867c93d753e538ba801286/image-35.jpg)








- Slides: 43

Linear Programming and Simplex Algorithm Reference: Numerical Recipe Sec. 10. 8

Content • • Linear programming problems Simplex algorithm QSOpt solver LP Applications – Collision detection – Melodic similarity – Underdetermined linear systems 2

The Diet Problem • Dietician preparing a diet consisting of two foods, A and B. A B Cost 0. 60 0. 40 Protein 20 30 Fat Carbohydrate 12 30 6 15 Minimum requirement: protein 60 g; fat 24 g; carbohydrate 30 g Looking for minimum cost diet 3

Linear Programming Cp. NLP subject to 4

The Problem Maximize Subject to N: dimension of x M: number of constraints (M = m 1+m 2+m 3) 5

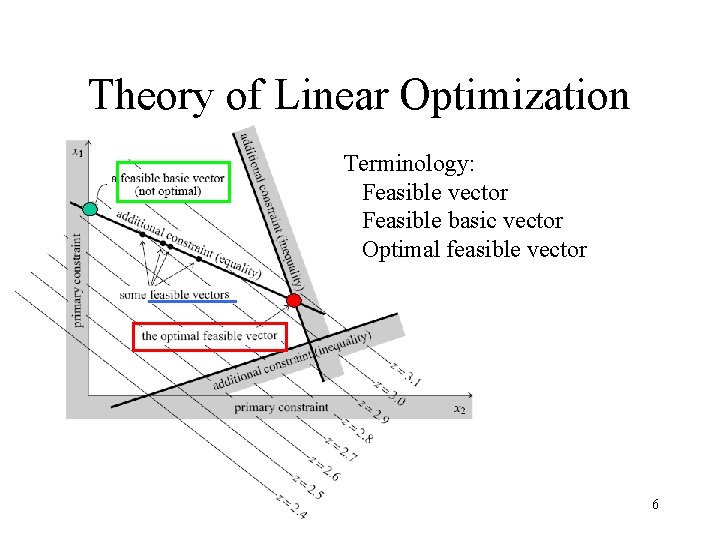
Theory of Linear Optimization Terminology: Feasible vector Feasible basic vector Optimal feasible vector 6

Theory (cont) • Feasible region is convex and bounded by hyperplanes • Feasible vectors that satisfy N of the original constraints as equalities are termed feasible basic vectors. • Optimal occur at boundary (gradient vector of objective function is always nonzero) • Combinatorial problem: determining which N constraints (out of the N+M constraints) would be satisfied by the optimal feasible vector 7

Simplex Algorithm (Dantzig 1948) • A series of combinations is tried to increase the objective function • Number of iterations less than O(max(M, N)) • Worst case complexity is exponential (in number of variables); yet has polynomial smoothed complexity (and works well in practice) 8

The Canonical Problem Maximize Subject to N: dimension of x M: number of constraints (M = m 1+m 2+m 3) I. III. 9

![QSopt ref Contains a GUI and a callable library 11 QSopt [ref] • Contains a GUI and a callable library 11](https://slidetodoc.com/presentation_image_h2/f65db55c44867c93d753e538ba801286/image-11.jpg)
QSopt [ref] • Contains a GUI and a callable library 11

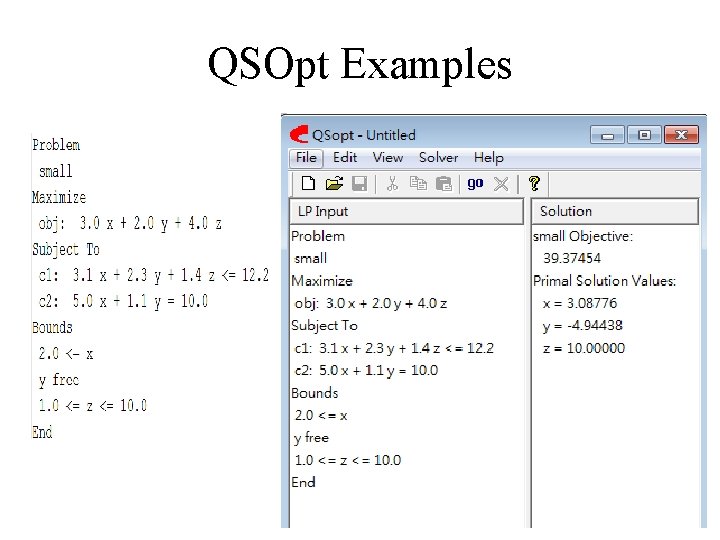
LP Format Example Problem small. Example Minimize obj: 0. 60 x 1 + 0. 40 x 2 Subject to c 1: 12 x 1 + 6 x 2 >= 24 30 x 1 + 15 x 2 >= 30 Somehow x 1 >= 0 x 2 >= 0 Doesn’t work!? Bounds 0 <= x 1 0 <= x 2 End BNF for QSOpt scripts 12

QSOpt Examples 13

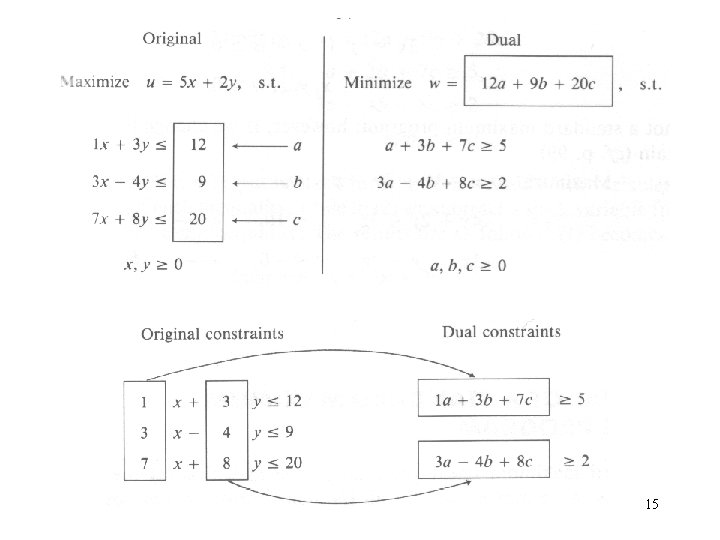
Duality • Primal problem • Dual problem 14

15

Duality • If a linear program has a finite optimal solution then so does the dual. Furthermore, the optimal values of the two programs are the same. • If either problem has an unbounded optimal solution, then the other problem has no feasible solutions. 16
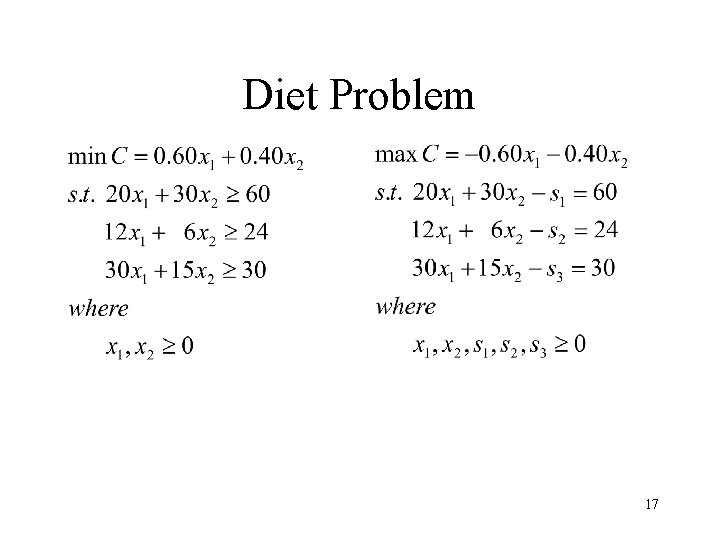
Diet Problem 17

Applications

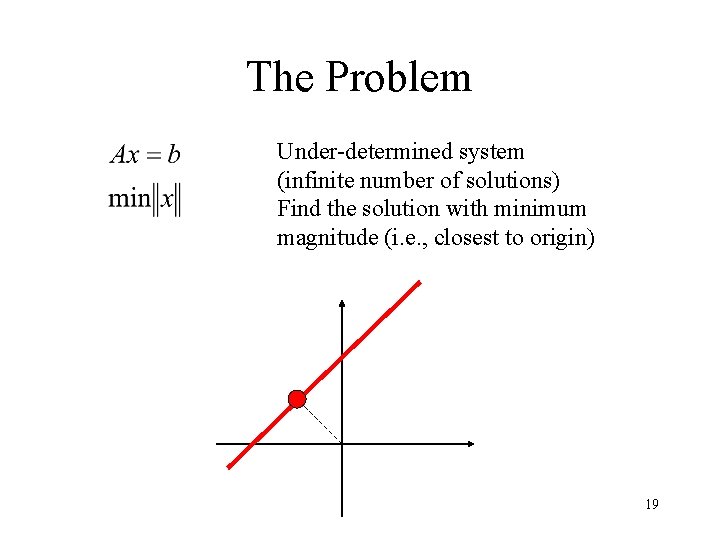
The Problem Under-determined system (infinite number of solutions) Find the solution with minimum magnitude (i. e. , closest to origin) 19

Example Approach 1: find complete solution (-2, 0, 0) subtract its projection along (1, -1, 1) (-2, 0, 0) (1, -1, 1) 20

Linear Programming Solution • Most simplex algorithm assume nonnegative variables • Set 21
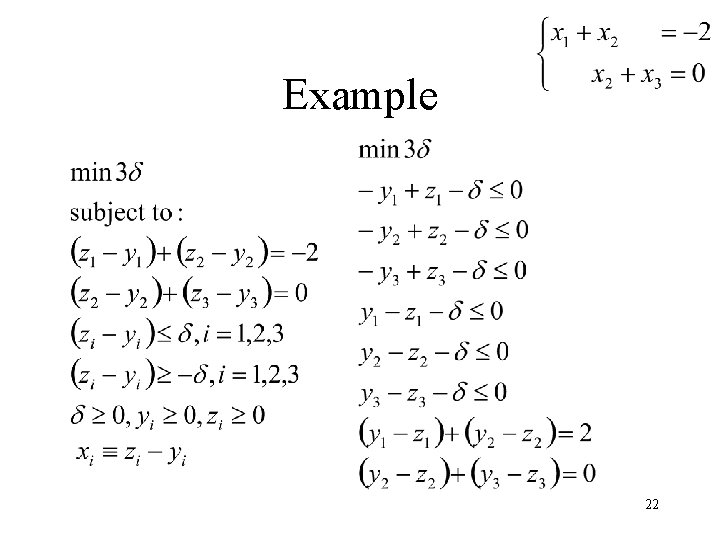
Example 22

Solved by QSopt The real minimum (-4/3, -2/3, 2/3) The LP constraint is not exactly ||x||2 (but ||x|| ) This problem can also be solved by SVD (singular value decomposition) 23

LP in CD (narrow phase, ref) • A pair of convex objects: each facet represented by the plane inequality aix+biy+ciz di • If two sets of inequality (from two convex objects) define a feasible region, then a collision is detected • The type of optimization (min|max) and the objective function used is irrelevant. 24

LP for CD Convert to dual problem for better efficiency(? !) 25

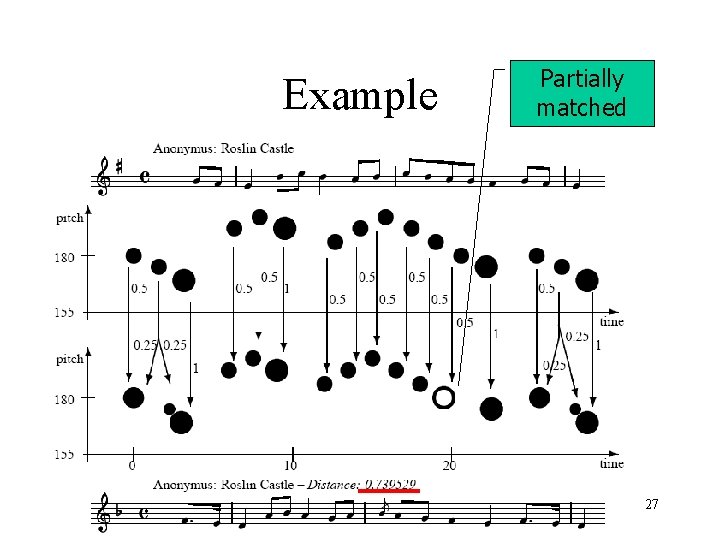
Transportation Distance as a Measure to Melodic Similarity Ref: Typke et al. 2003

Example Partially matched 27

Earth Mover Distance 28

EMD as Linear Program Solve by simplex algorithm 29

EMD for Melodic Similarity • Ground distance: Euclidean distance • Scale time coordinate (so that they are comparable) • Transposition: transpose one of the melodies so that the weighted average pitch is equal (not optimum but acceptable) 30

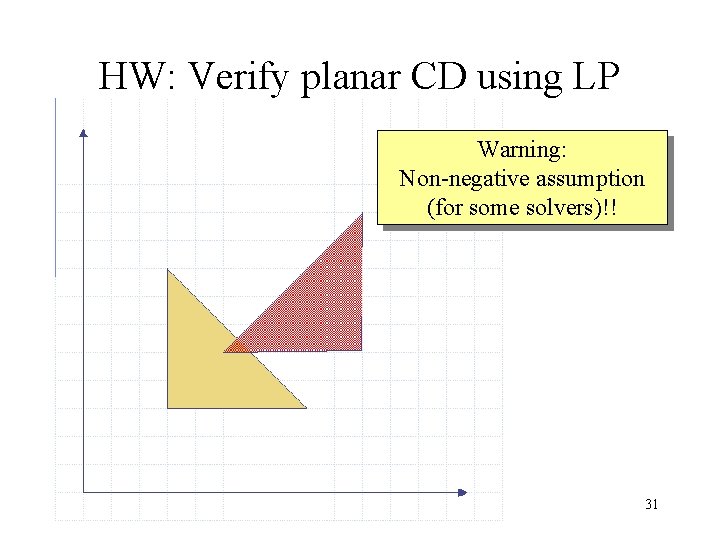
HW: Verify planar CD using LP Warning: Non-negative assumption (for some solvers)!! 31

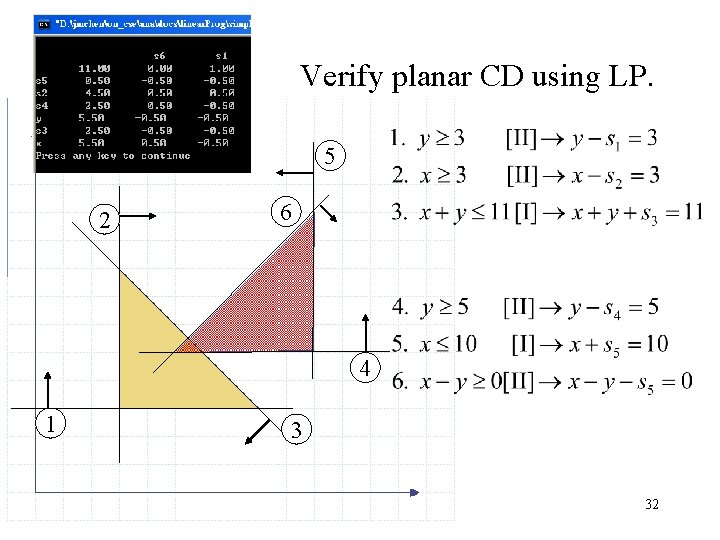
Verify planar CD using LP. 5 2 6 4 1 3 32

LP Solvers • Lp_solve: MILP • QSopt • GLPK 33

![QSopt ref Contains a GUI and a callable library 35 QSopt [ref] • Contains a GUI and a callable library 35](https://slidetodoc.com/presentation_image_h2/f65db55c44867c93d753e538ba801286/image-35.jpg)
QSopt [ref] • Contains a GUI and a callable library 35

LP Format Example Problem small. Example Minimize obj: 0. 60 x 1 + 0. 40 x 2 Subject to c 1: 12 x 1 + 6 x 2 >= 24 30 x 1 + 15 x 2 >= 30 [weird] Somehow x 1 >= 0 x 2 >= 0 Doesn’t work!? Bounds 0 <= x 1 0 <= x 2 End 36

LP format BNF definition 1 37

LP format BNF definition 2 38

QSOpt API

Scenario: Read and Solve 40

Accessing a Solution • value: objective function • x: solution vector (columns) • pi: dual variables • slack: slack variables • rc: reduced cost • In our applications, we don’t really care about pi, slack, and rc. • Set them to NULL 41

QS_MAX or QS_MIN cmatind 0 0 0 1 1 # of nonzeros in jth column Location of start entry 42

Modify an LP Problem • • • QSnew_row QSadd_rows QSnew_col QSadd_cols QSdelete_row QSdelete_col QSchange_coef QSchange_objcoef QSchange_rhscoef QSchange_sense • See reference manuals for more details (Ch. 5) • Use QSwrite_prob to verify the change 43