Linear Patterns www mathsrevision com MTH 3 13

Linear Patterns www. mathsrevision. com MTH 3 -13 a Sequences & Patterns Simple Linear Graphs Complicated Linear Patterns Linear Graphs Flower Beds

Starter Questions www. mathsrevision. com MTH 3 -13 a 6 cm 10 cm 114 Sunday, September 5, 2021 Created by Mr. Lafferty @www. mathsrevision. com o 2

Square and Triangular Numbers www. mathsrevision. com MTH 3 -13 a Learning Intention Success Criteria 1. We are revising square and triangular number. 1. To understand what square and triangular numbers are. 2. Calculate the first 10 square and triangular numbers. Sunday, September 5, 2021 Created by Mr. Lafferty @www. mathsrevision. com 3

Square Numbers www. mathsrevision. com MTH 3 -13 a Write down the next square number 1 12 4 22 9 32 16 42 Write down the first 10 square numbers. 1 4 9 16 25 36 49 64 81 100 05 -Sep-21 Created by Mr. Lafferty Math Dept

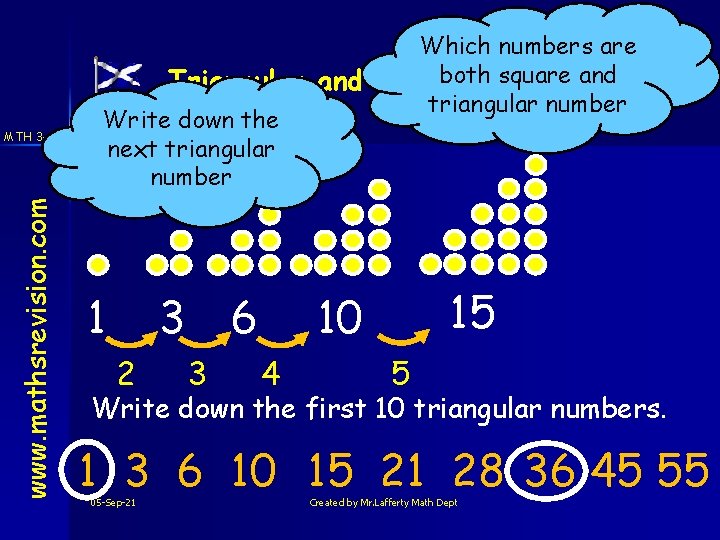
www. mathsrevision. com MTH 3 -13 a Which numbers are both square and Triangular and square Numbers triangular number Write down the next triangular number 1 3 2 6 3 15 10 4 5 Write down the first 10 triangular numbers. 1 3 6 10 15 21 28 36 45 55 05 -Sep-21 Created by Mr. Lafferty Math Dept

Linear Patterns www. mathsrevision. com MTH 3 -13 a Now try TJ 3 b Ex 1 Ch 4 (page 36) 05 -Sep-21 Created by Mr. Lafferty Maths Dept.

Starter Questions www. mathsrevision. com MTH 3 -13 a Q 1. Q 2. Calculate Area and perimeter 30% of 200 Q 3. Q 4. 3 cm 5 cm 4 cm 2 cm If a = 1 , b = 2 and c = 4 Find

Simple Linear Patterns using diagrams and tables www. mathsrevision. com MTH 3 -13 a Learning Intention 1. We are learning to use tables to help us come up with formulae for Simple Linear Patterns. Success Criteria 1. Find the difference in a pattern. 2. Write down formula

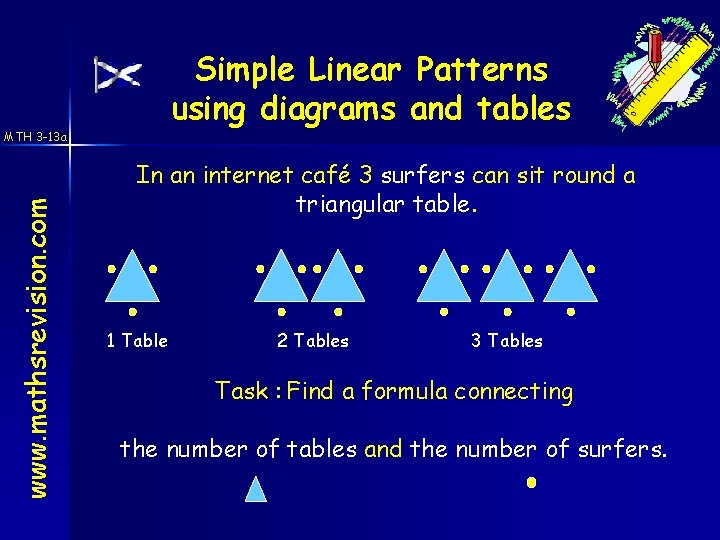
Simple Linear Patterns using diagrams and tables www. mathsrevision. com MTH 3 -13 a In an internet café 3 surfers can sit round a triangular table. 1 Table 2 Tables 3 Tables Task : Find a formula connecting the number of tables and the number of surfers.

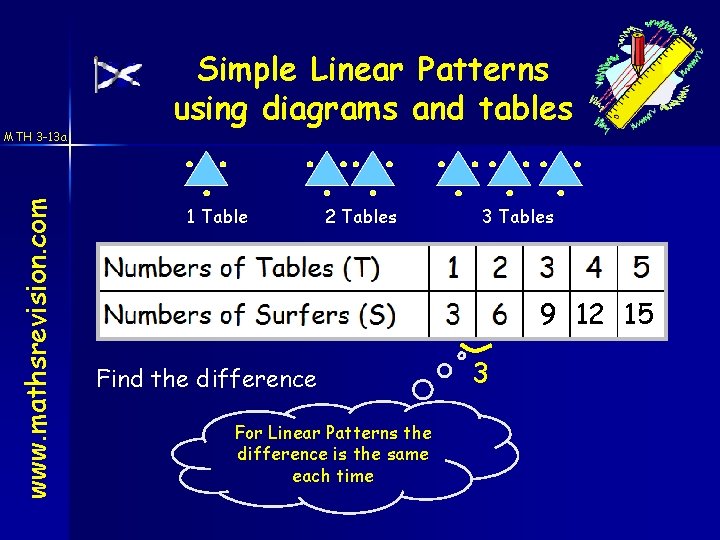
www. mathsrevision. com MTH 3 -13 a Simple Linear Patterns using diagrams and tables 1 Table 2 Tables 3 Tables 9 12 15 Find the difference For Linear Patterns the difference is the same each time 3

www. mathsrevision. com MTH 3 -13 a Can you write down the formula connecting Simple Linear Patterns the number of surfers and the number of tables. using diagrams and tables 9 12 15 HINT : Let the number of surfers be the letter S and the number of tables be the letter T S=3 x. T S = 3 T

www. mathsrevision. com MTH 3 -13 a Simple Linear Patterns using diagrams and tables Key-Points 1. Fill in the table 2. Find the difference 3. Use the difference to write down the formula

Linear Patterns www. mathsrevision. com MTH 3 -13 a Now try TJ 3 b Ex 2 Q 1 to Q 5 Ch 4 (page 38) 05 -Sep-21 Created by Mr. Lafferty Maths Dept.

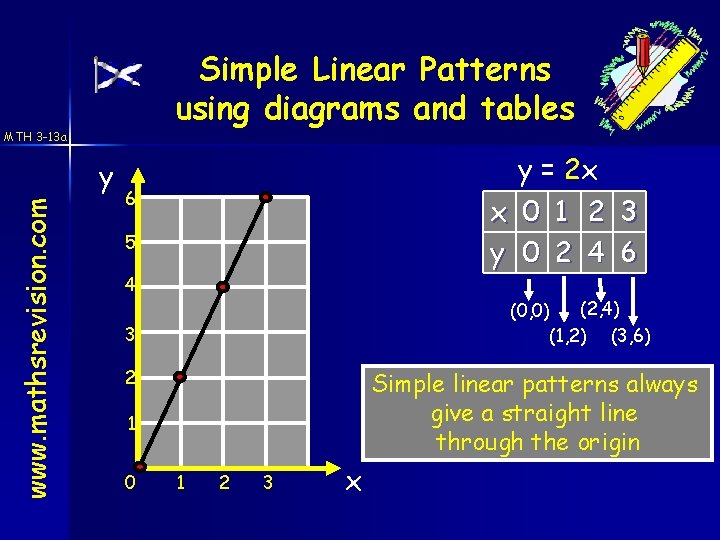
Simple Linear Patterns using diagrams and tables MTH 3 -13 a www. mathsrevision. com y y = 2 x 6 x 0 1 2 3 y 0 2 4 6 5 4 (2, 4) (0, 0) (1, 2) (3, 6) 3 2 Simple linear patterns always give a straight line through the origin 1 0 1 2 3 x

Linear Patterns www. mathsrevision. com MTH 3 -13 a Now try TJ 3 b Ex 2 Q 6 to Q 7 Ch 4 (page 40) 05 -Sep-21 Created by Mr. Lafferty Maths Dept.

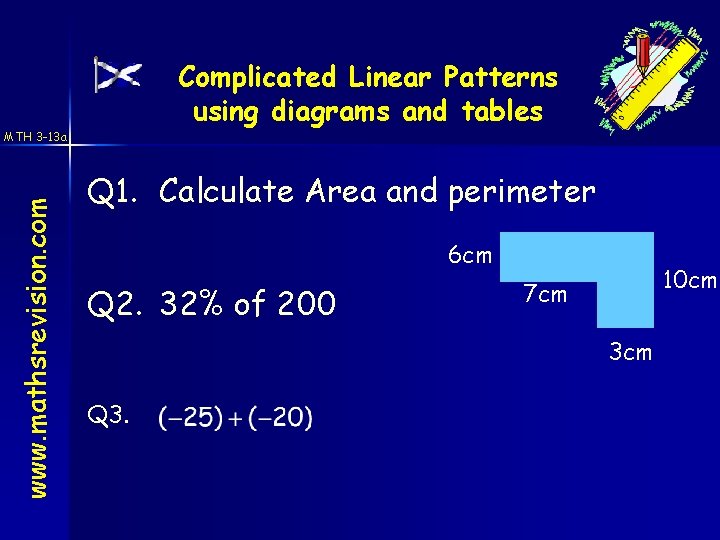
Complicated Linear Patterns using diagrams and tables www. mathsrevision. com MTH 3 -13 a Q 1. Calculate Area and perimeter 6 cm Q 2. 32% of 200 10 cm 7 cm 3 cm Q 3.

Complicated Linear Patterns using diagrams and tables www. mathsrevision. com MTH 3 -13 a Learning Intention 1. We are learning to use tables to help us come up with formulae for complicated Linear Patterns using diagrams and tables. Success Criteria 1. Find the difference value in patterns. 2. Calculate correction factor 3. Write down formula using steps 1 & 2 above

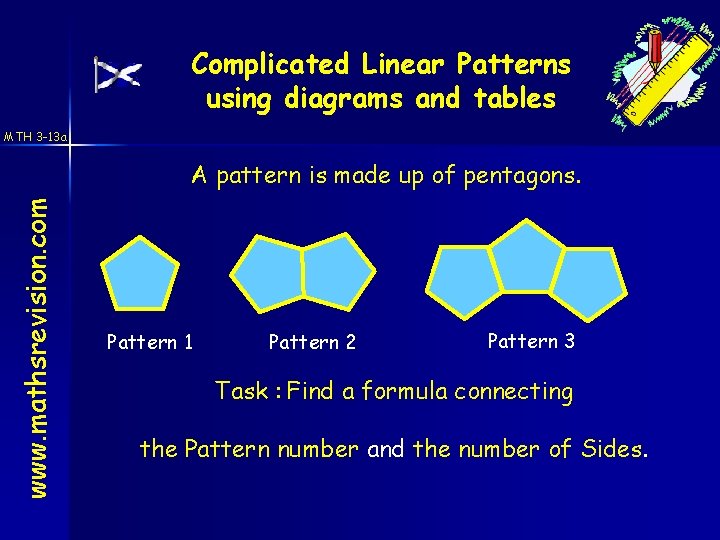
Complicated Linear Patterns using diagrams and tables MTH 3 -13 a www. mathsrevision. com A pattern is made up of pentagons. Pattern 1 Pattern 2 Pattern 3 Task : Find a formula connecting the Pattern number and the number of Sides.

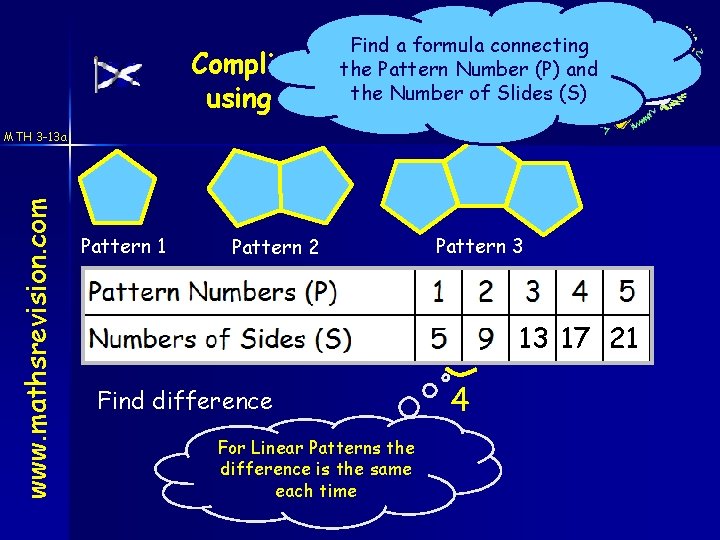
Find a formula connecting Complicatedthe. Linear Patterns Pattern Number (P) and the Number Slides (S) using diagrams and of tables www. mathsrevision. com MTH 3 -13 a Pattern 1 Pattern 2 Pattern 3 13 17 21 Find difference For Linear Patterns the difference is the same each time 4

MTH 2 -13 a & MTH 3 -13 a Complicated Linear Patterns using diagrams and tables www. mathsrevision. com MTH 3 -13 a 13 17 21 Part of the formula Correction factor “add on 1” S = 4 P + 1

Complicated Linear Patterns using diagrams and tables www. mathsrevision. com MTH 3 -13 a Key-Points 1. Fill in the table 2. Find the difference 3. Write down part of formula 4. Find the correction factor and then write down the full formula

Linear Patterns www. mathsrevision. com MTH 3 -13 a Now try TJ 3 b Ex 3 Q 1 to Q 6 Ch 4 (page 41) 05 -Sep-21 Created by Mr. Lafferty Maths Dept.

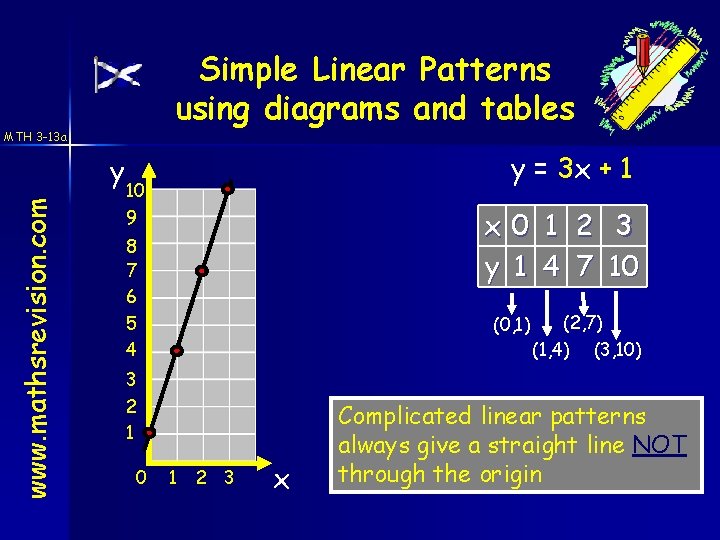
Simple Linear Patterns using diagrams and tables MTH 3 -13 a www. mathsrevision. com y y = 3 x + 1 10 x y 9 8 7 6 5 4 (0, 1) 3 2 1 0 0 1 1 2 3 x 1 4 2 7 3 10 (2, 7) (1, 4) (3, 10) Complicated linear patterns always give a straight line NOT through the origin

Have you updated your Learning Log ? Linear Patterns www. mathsrevision. com MTH 3 -13 a Now try TJ 3 b Ex 3 Q 7 Q 8 Ch 4 (page 44) Are you on Target ? I can ? 05 -Sep-21 Created by Mr. Lafferty Maths Dept.

Flower Bed Investigation www. mathsrevision. com MTH 3 -13 a David is designing a flower bed pattern for the local garden show. He wants to use regular hexagonal shapes for the bed and slabs. This is the flower bed shape This is a slab shape

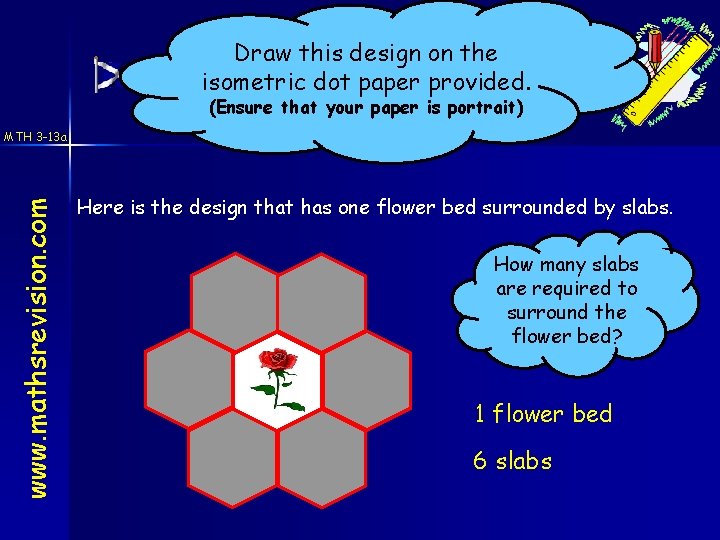
Draw this design on the Flower Bed Investigation isometric dot paper provided. (Ensure that your paper is portrait) www. mathsrevision. com MTH 3 -13 a Here is the design that has one flower bed surrounded by slabs. How many slabs are required to surround the flower bed? 1 flower bed 6 slabs

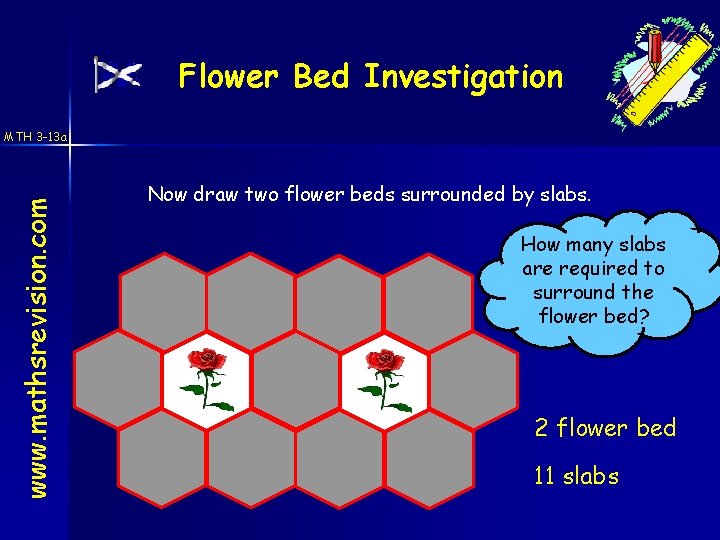
Flower Bed Investigation www. mathsrevision. com MTH 3 -13 a Now draw two flower beds surrounded by slabs. How many slabs are required to surround the flower bed? 2 flower bed 11 slabs

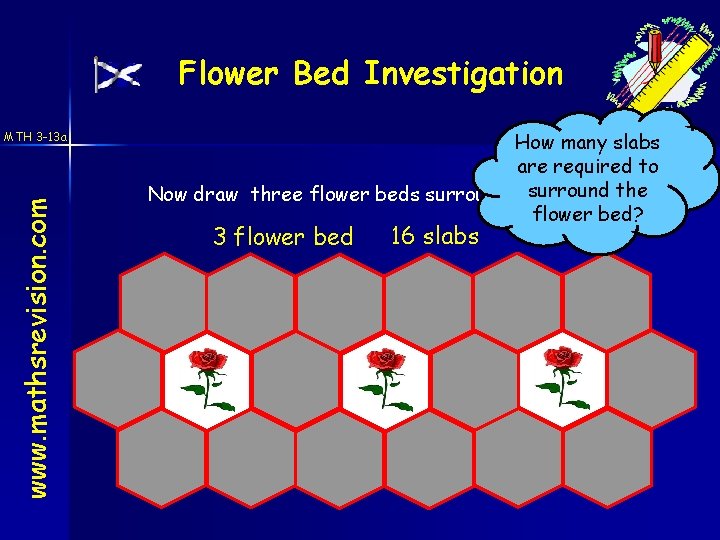
Flower Bed Investigation www. mathsrevision. com MTH 3 -13 a How many slabs are required to Now draw three flower beds surroundedsurround by slabs. the flower bed? 3 flower bed 16 slabs

Flower Bed Investigation www. mathsrevision. com MTH 3 -13 a Task In your group discuss how best to record these results and work out a formula to calculate the number of slabs for given number of flower beds. As a group you are required to hand in a single solution for this task showing all working.

Flower Bed Investigation www. mathsrevision. com MTH 3 -13 a 6 11 16 21 s = 5 f + 1 126 How many hexagonal slabs are needed for 25 flower beds. If we had 76 available slabs how many flower beds could we surround 15

Flower Bed Investigation www. mathsrevision. com MTH 3 -13 a Task What is the maximum number of flower beds you could surround if you had 83 slabs 16

Flower Bed Investigation www. mathsrevision. com MTH 3 -13 a Homework Now align the flower beds vertically and investigate if the formula is still the same?

www. mathsrevision. com MTH 3 -13 a Vertical Flower Bed Investigation 6 10 14 18 s = 4 f + 2