Linear Motion by Mrs Walker x vavet delta

Linear Motion by Mrs. Walker

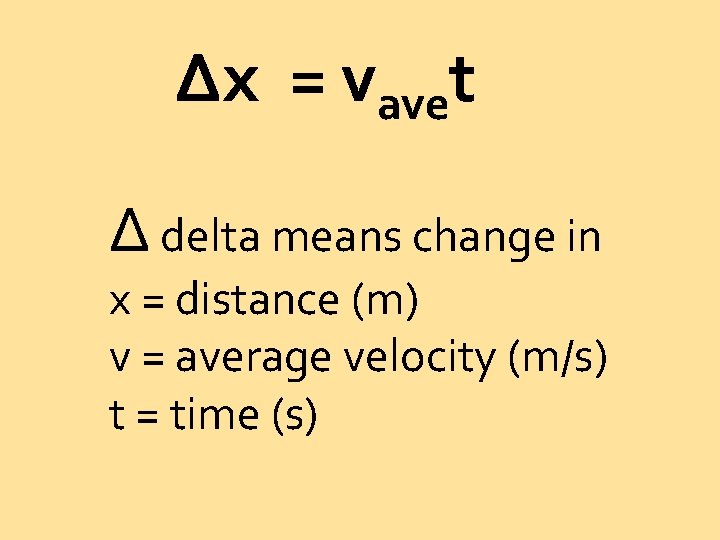
Δx = vavet Δ delta means change in x = distance (m) v = average velocity (m/s) t = time (s)

Want an “A”? Here’s the secret: Learn the units (like m/s) right away! Knowing the formulas is like knowing which tool to use out of the tool box… pliers or hammer….

If you drive the 37. 9 miles from Plainfield to Chicago and are going 55 mph, how long would it take you to get there? known x=37. 9 mi v=55 mi/hr unknown t Δx = vavet 37. 9 mi = 55 mi/hr (t) 37. 9 mi = 0. 6891 x 60 = 55 mi/hr 41. 35 min

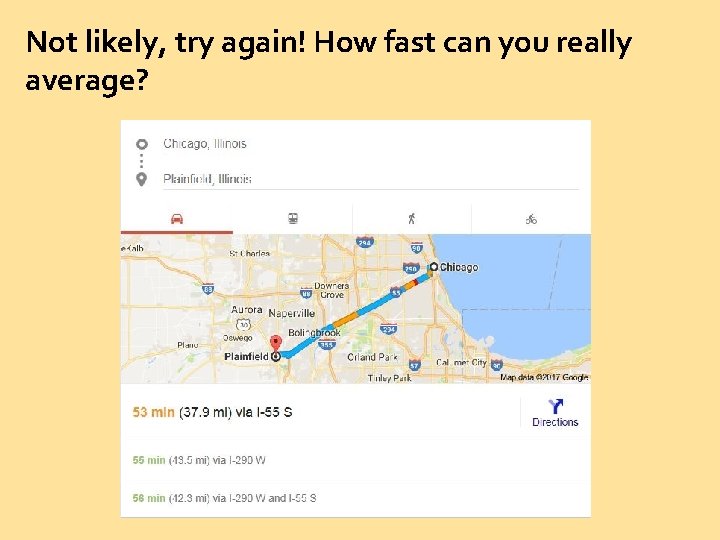
Not likely, try again! How fast can you really average?

Pair & Share: Find out …. . known x=37. 9 mi t = 53 minutes unknown v (switch this to hours 1 st) Δx = vavet 37. 9 mi = v (53 min) (60 min/h) 37. 9 mi = 42. 9 m/h 0. 883 h

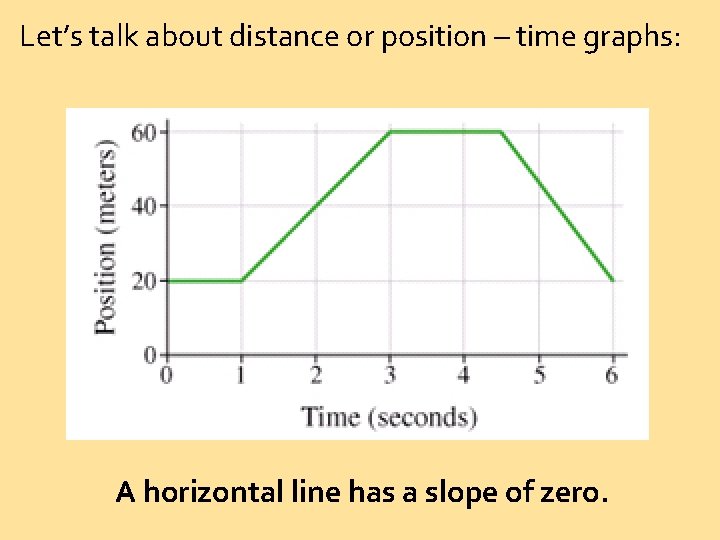
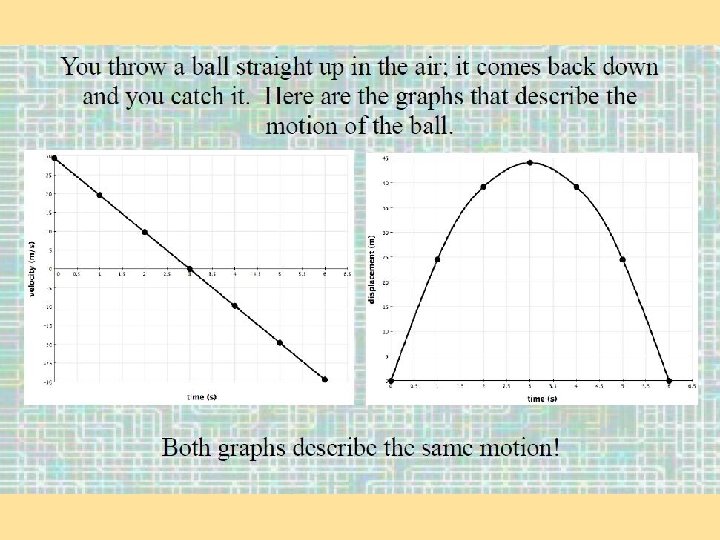
Let’s talk about distance or position – time graphs: A horizontal line has a slope of zero.

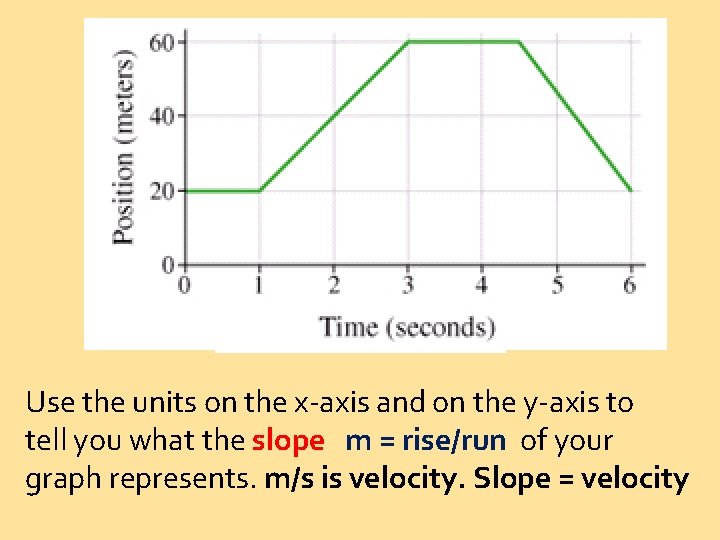
Use the units on the x-axis and on the y-axis to tell you what the slope m = rise/run of your graph represents. m/s is velocity. Slope = velocity

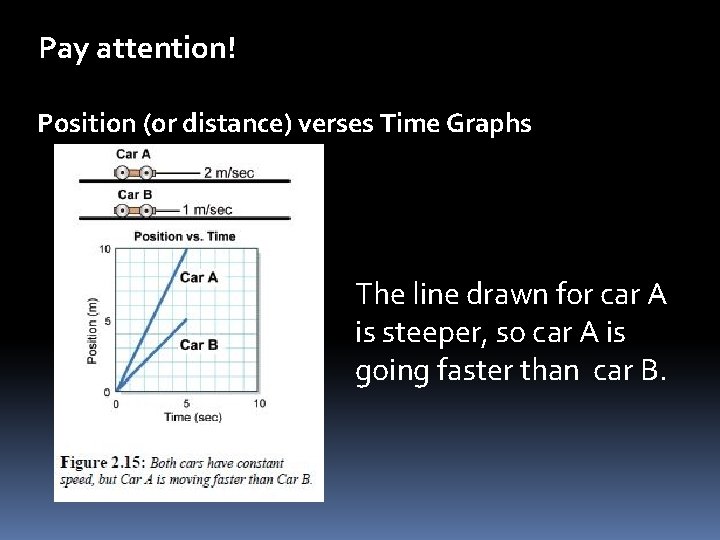
Pay attention! Position (or distance) verses Time Graphs The line drawn for car A is steeper, so car A is going faster than car B.

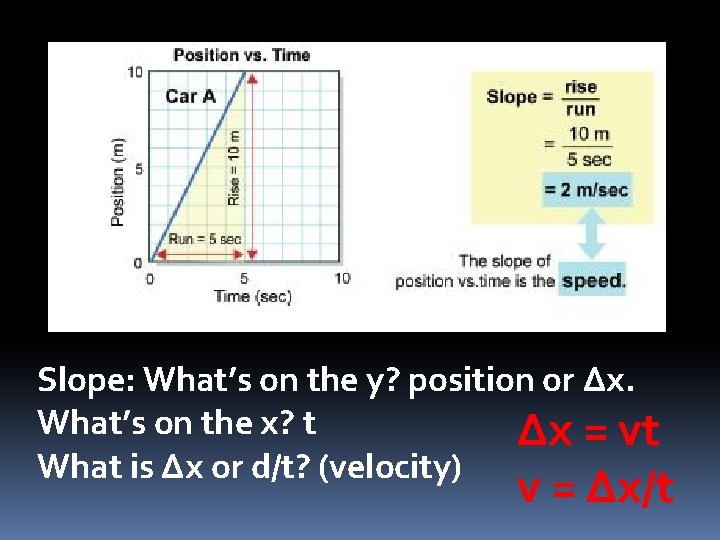
Slope: What’s on the y? position or Δx. What’s on the x? t Δx = vt What is Δx or d/t? (velocity) v = Δx/t

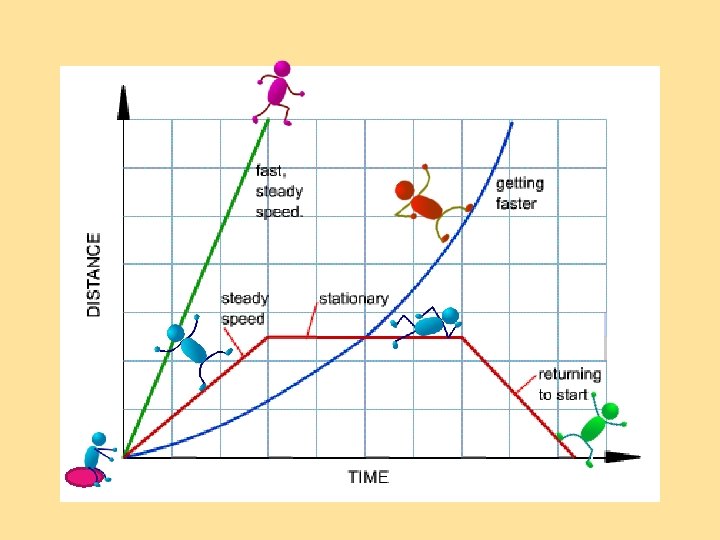
http: //www. physicsclassroom. com/mmedia/kinema/fs. cfm

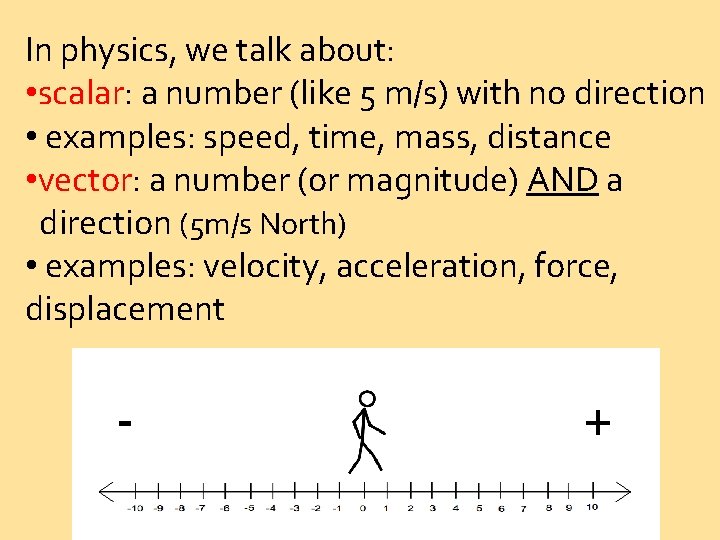
In physics, we talk about: • scalar: a number (like 5 m/s) with no direction • examples: speed, time, mass, distance • vector: a number (or magnitude) AND a direction (5 m/s North) • examples: velocity, acceleration, force, displacement - +

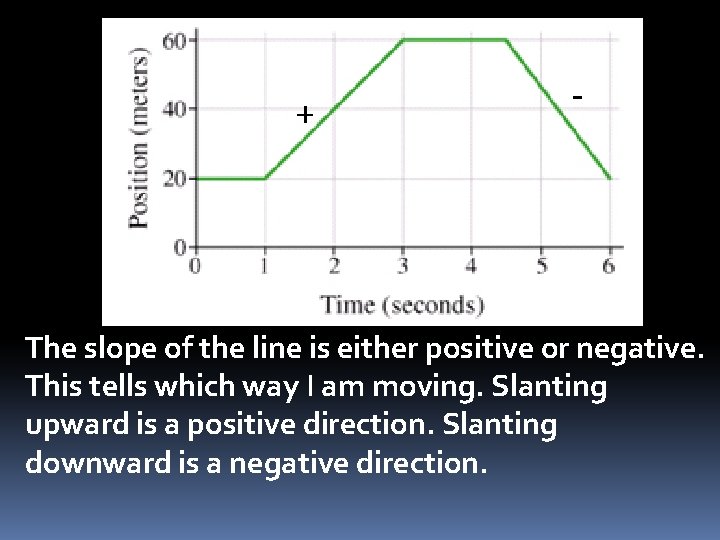
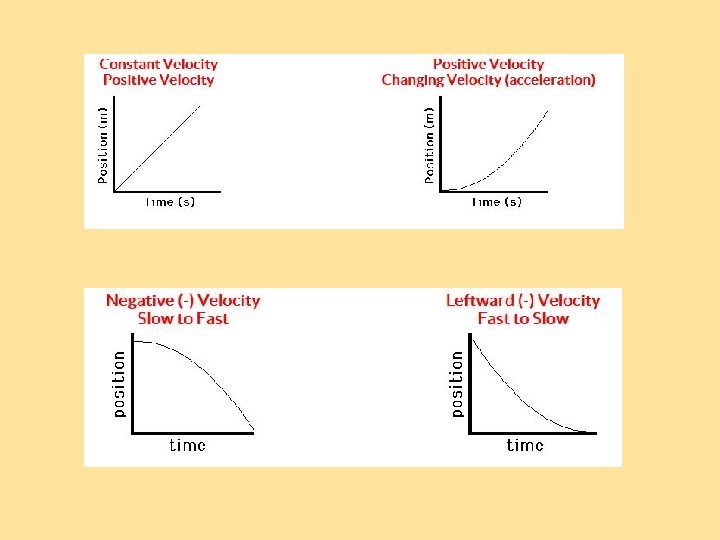
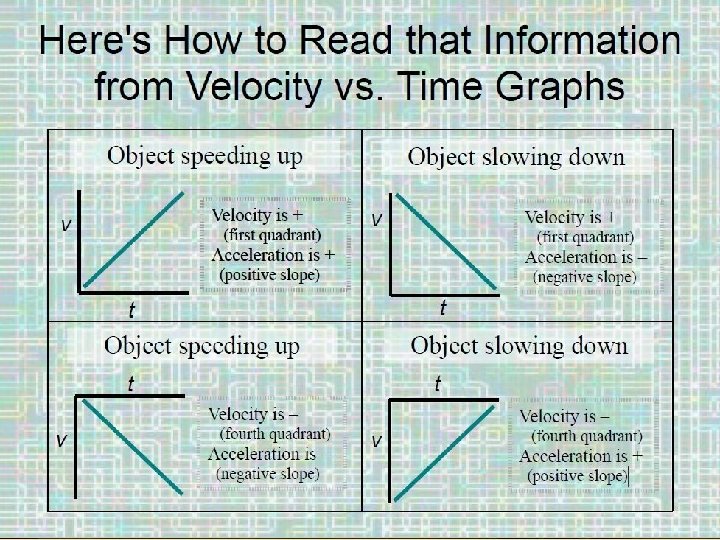
+ - The slope of the line is either positive or negative. This tells which way I am moving. Slanting upward is a positive direction. Slanting downward is a negative direction.

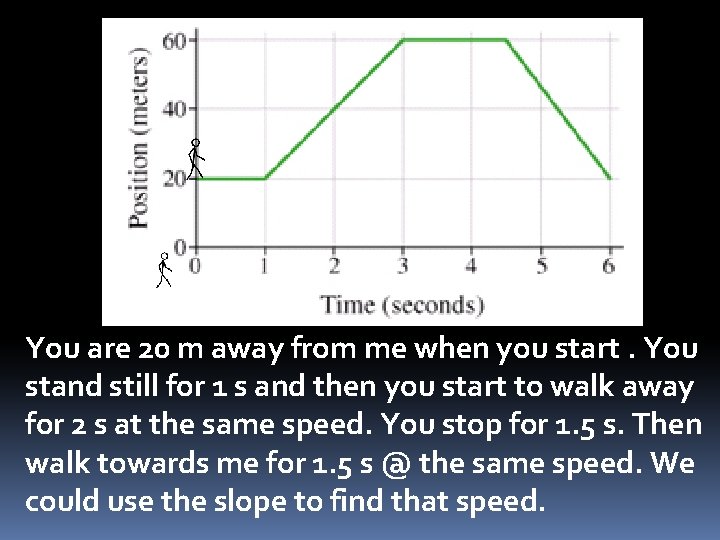
You are 20 m away from me when you start. You stand still for 1 s and then you start to walk away for 2 s at the same speed. You stop for 1. 5 s. Then walk towards me for 1. 5 s @ the same speed. We could use the slope to find that speed.

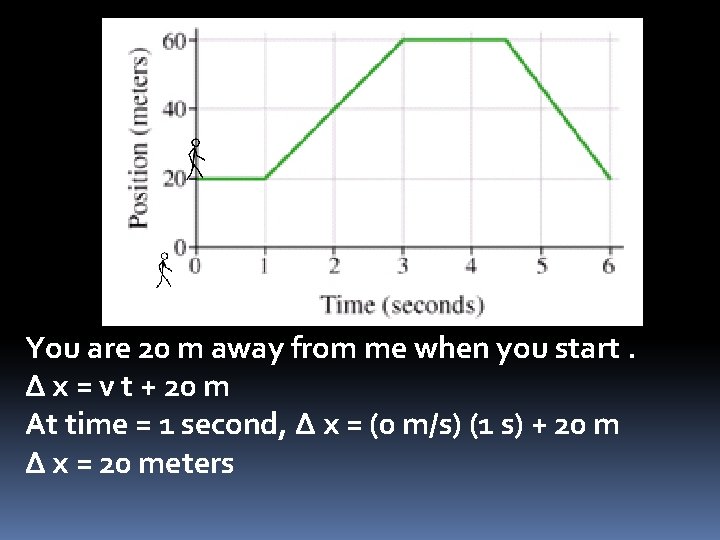
You are 20 m away from me when you start. Δ x = v t + 20 m At time = 1 second, Δ x = (0 m/s) (1 s) + 20 m Δ x = 20 meters

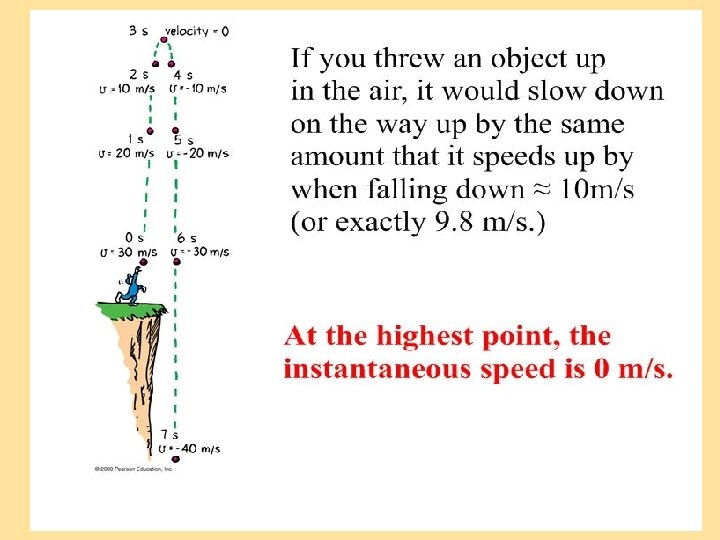
We call this “an oil drop diagram”. Pretend you are at Jiffy Lube having your oil changed and they don’t tighten the screw enough so you drip oil as you drive down the road. Can you tell when you were parked? Now tell me about your speed as you leave.

Now let’s talk about acceleration: Acceleration is the rate at which your velocity changes. You can be either speeding up, or slowing down. Both are acceleration. A plus sign (+) shows acceleration. A negative sign (-) shows deceleration. The standard unit is m/s 2.

v = at m/s = m (s) 2 s s s of 2 m/s (s) a=v t

A car is moving at a constant speed and then accelerates at 2 m/s 2 for 8 seconds. How fast is the car going after accelerating? known a = 2 m/s 2 t=8 s v=at unknown v v = 2 m/s 2 (8 s) v = 16 m/s

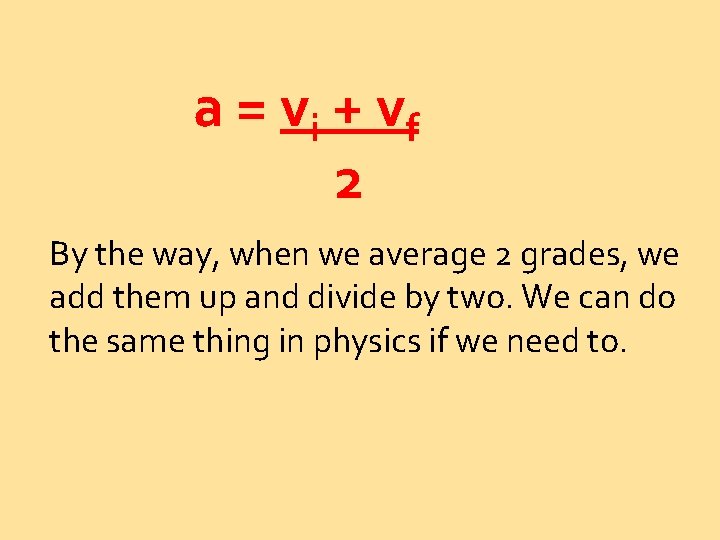
a = vi + v f 2 By the way, when we average 2 grades, we add them up and divide by two. We can do the same thing in physics if we need to.

An airplane accelerates down the runway at 2. 5 m/s 2. The plane’s takeoff speed is 70 m/s. How long is the runway? Known a = 2. 5 m/s 2 vi = 0 m/s vf = 70 m/s Unknown Δx v=at 70 m/s = 2. 5 m/s 2 (t) t = 28 s Δx = vf t Δ x = 70 m/s (28 s) Δ x = 1, 960 m

Velocity is a vector. A car that turns in a circular path is accelerating because the direction is changing. A vector includes both speed and direction. It doesn’t matter if you have the car locked in cruise control at the same speed. You ARE accelerating.

Now remember…. when we talk about acceleration, don’t forget… there is + a and – a. (Acceleration and deceleration. ) Let’s figure out the following graph together.

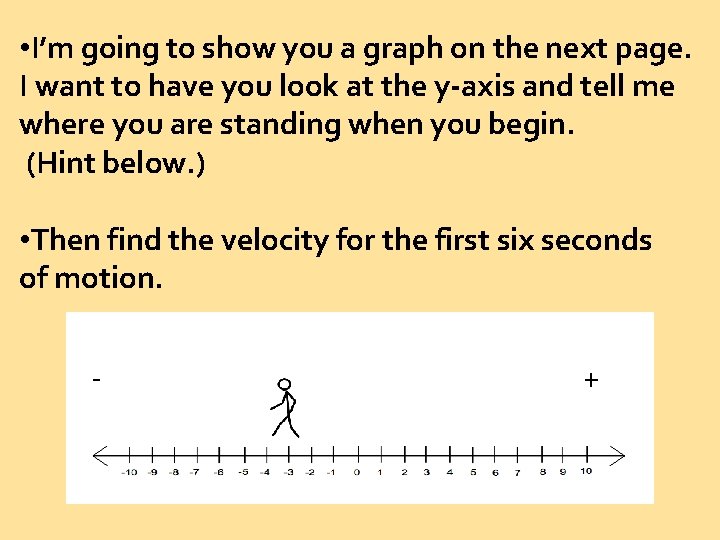
• I’m going to show you a graph on the next page. I want to have you look at the y-axis and tell me where you are standing when you begin. (Hint below. ) • Then find the velocity for the first six seconds of motion. - +

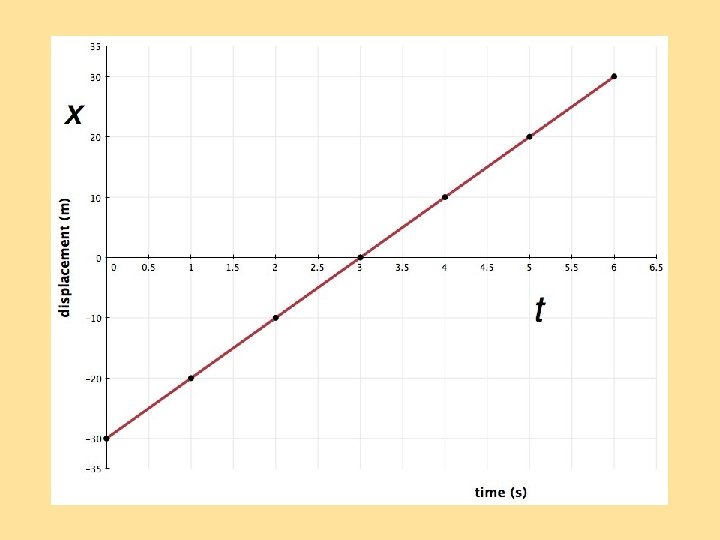
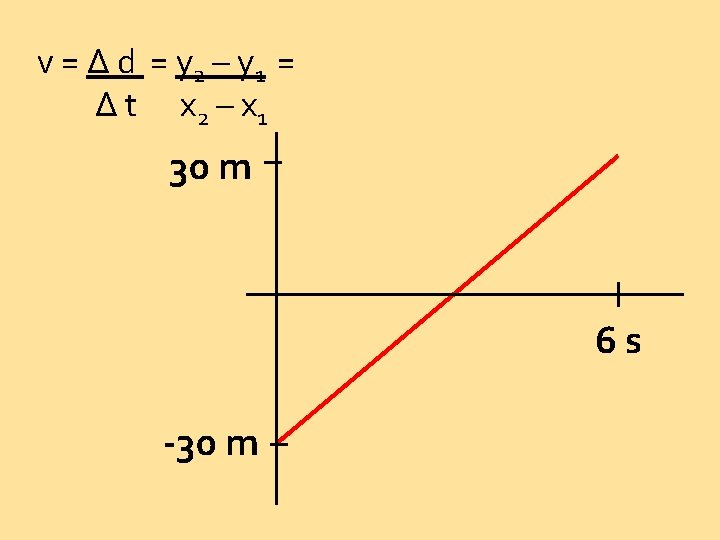
v = Δ d = y 2 – y 1 = Δ t x 2 – x 1 30 m 6 s -30 m

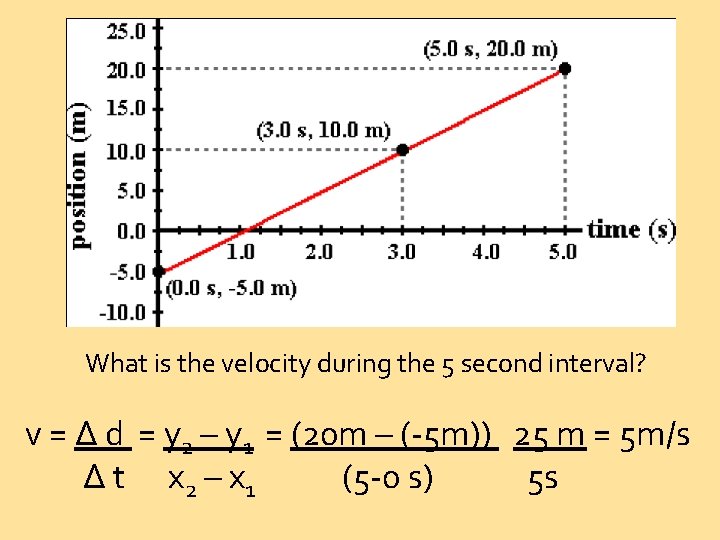
What is the velocity during the 5 second interval? v = Δ d = y 2 – y 1 = (20 m – (-5 m)) 25 m = 5 m/s Δ t x 2 – x 1 (5 -0 s) 5 s

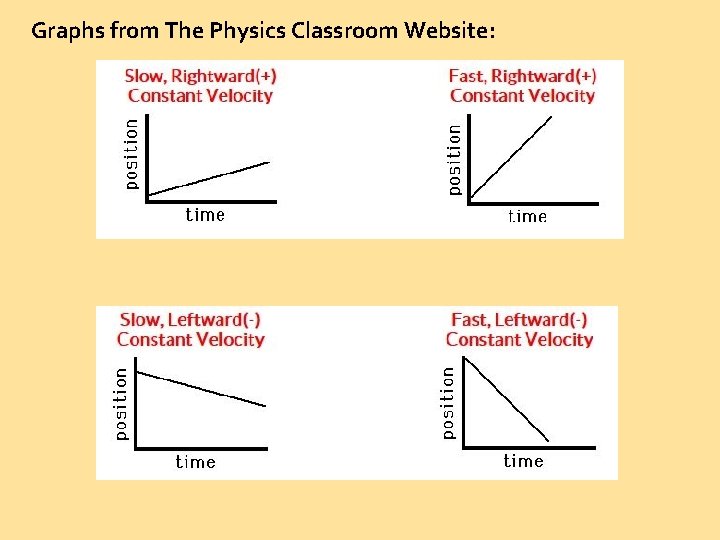
Graphs from The Physics Classroom Website:

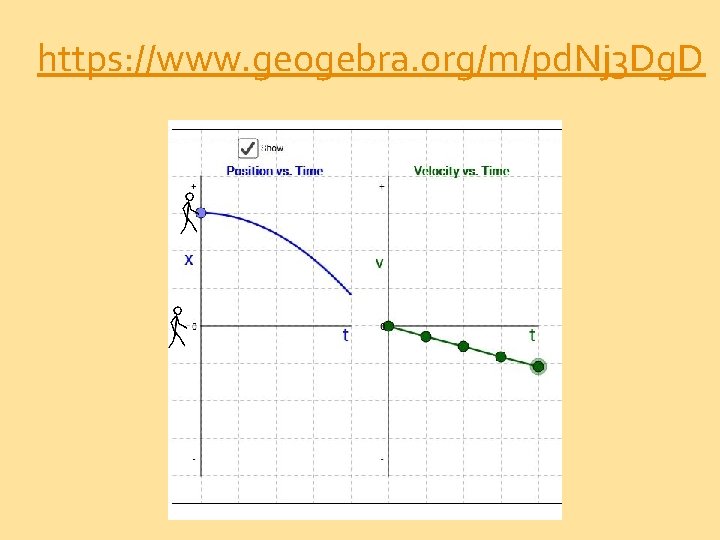
https: //www. geogebra. org/m/pd. Nj 3 Dg. D

Positive Velocity and Negative Acceleration • If you move in the positive direction (right) you have a positive velocity. • If you are slowing down, then this is negative acceleration and is shown as moving leftward. http: //www. physicsclassroom. com/mmedia/kinema/pvna. cfm

Speeding Up or Slowing Down? Warning: Many people mistakenly believe that a positive acceleration means the object is speeding up and a negative acceleration means the object is slowing down. Here's the truth: If the numerical values of an object's velocity and acceleration have the same sign (both positive or both negative), then the object is speeding up. If the velocity and acceleration have opposite signs (one of positive and the other is negative), then the object is slowing down.

Vi and Vo mean the same thing. Vf = Vo + at 2 Xf = Xo + Vot + 1/2 at 2 2 Vf = Vo + 2 aΔX

Kulula Airlines

An airplane accelerates down the runway at 2. 5 m/s 2. The plane’s takeoff speed is 70 m/s. How long is the runway? (We saw this previously!) Known a = 2. 5 m/s 2 vi = 0 m/s vf = 70 m/s Unknown Δx Vf = 2 2 Vo + 2 aΔX (70 m/s)2= (0 m/s)2 + 2 (2. 5 m/s 2) Δx 4900 = 980 meters 2(2. 5)

A car is driving down the road at 15 m/s at t = 0 sec. The car slows down at a rate of 3 m/s 2. How long will it take the car to stop? Vf = Vi + at Known vf = 0 m/s vi or vo = 15 m/s a = - 3 m/s 2 Unknown t 0 m/s = 15 m/s + -3 m/s 2 (t) -15 m/s = 2 -3 m/s (t) 5 s=t

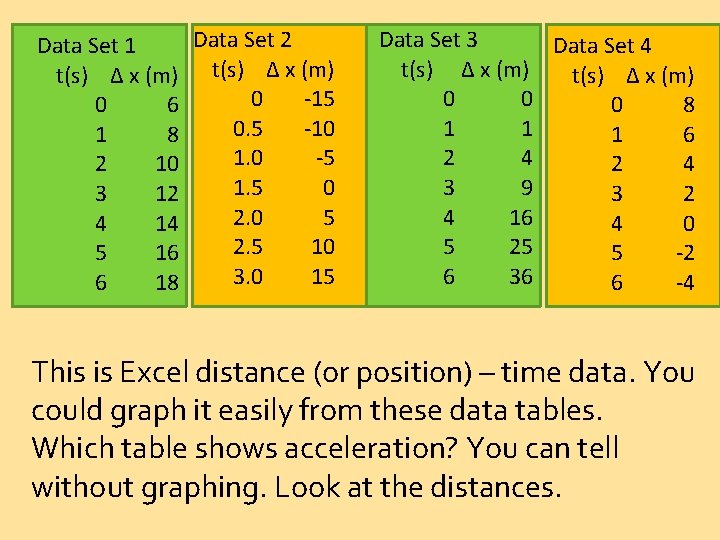
Data Set 2 Data Set 1 t(s) Δ x (m) 0 -15 0 6 0. 5 -10 1 8 1. 0 -5 2 10 1. 5 0 3 12 2. 0 5 4 14 2. 5 10 5 16 3. 0 15 6 18 Data Set 3 Data Set 4 t(s) Δ x (m) 0 0 0 8 1 1 1 6 2 4 3 9 3 2 4 16 4 0 5 25 5 -2 6 36 6 -4 This is Excel distance (or position) – time data. You could graph it easily from these data tables. Which table shows acceleration? You can tell without graphing. Look at the distances.

The oil drop diagram returns! Do you realize that with a 90 degree rotation, the oil drop diagram is something that you are already very familiar with?

Planet Moon Mercury Earth Jupiter Acceleration (g) due to gravity m/s 2 1. 62 3. 7 9. 8 24. 79 A basketball is dropped from a 25 m tall ladder. If the ball takes 2. 2588 seconds to reach the floor, what planet is it on?

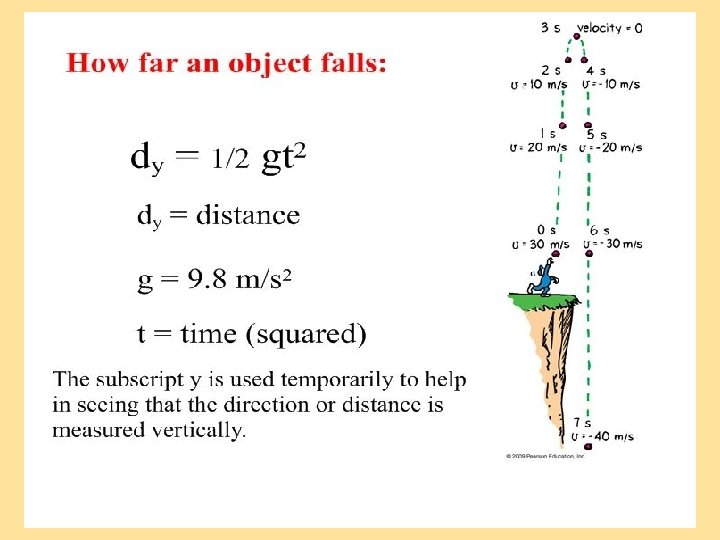
Known xf = 25 m xo = 0 m Vo = 0 m/s t = 2. 2588 s Unknown g or a Xf = Xo + Vot + 1/2 at 2 2 25 m = ½ a (2. 2588 s) 25 m (2/1) = ½ (2/1)( 5. 1020 s 2 ) 50/ 5. 1020 = 9. 8 m/s 2

Planet Moon Mercury Earth Jupiter Acceleration (g) due to gravity m/s 2 1. 62 3. 7 9. 8 24. 79 A basketball is dropped from a 25 m tall ladder. If the ball takes 2. 2588 seconds to reach the floor, what planet is it on?