Linear Momentum Newtons Laws of Motion First law

Linear Momentum

Newton’s Laws of Motion • First law • Second law • Third law

Work Done by a Force

Terms of Reference • Momentum: • Force: – for constant mass m – for constant velocity v

– if both mass and velocity vary with time • Impulse: • for constant mass: • for constant force:

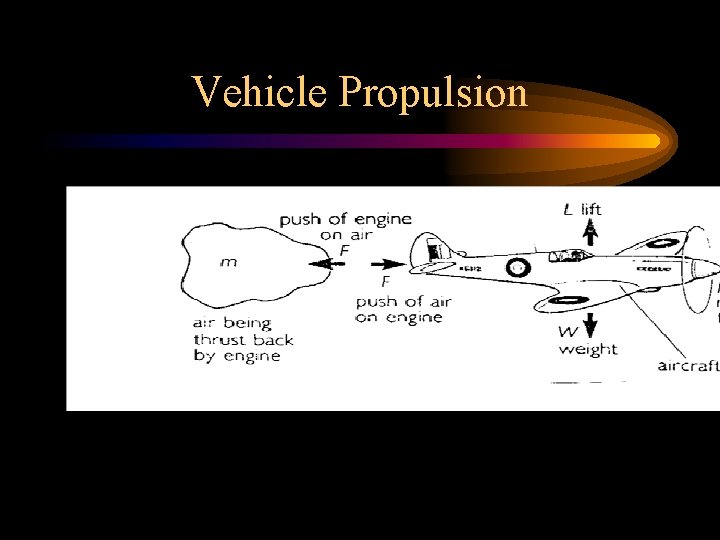
Vehicle Propulsion

Conservation of Linear Momentum • If no external forces act on a system of colliding objects, the total momentum of the objects remains constant. • Air-track experiment:

Collision • Elastic collisions: – k. e. is conserved – occur very often between atom-sized particles – occur when no contact is made for everyday-sized objects

Collision (cont’d) • Inelastic collisions: – k. e. is not conserved – common type of collision on a macroscopic scale – completely inelastic collision: two bodies stick together after impact Simulation

Collision (cont’d) • Explosive collisions: – potential energy were released – an increase in k. e. – usually occurs in explosions

Energy Changes in a Collision • Perfectly Inelastic Collision • Proof:

Proof Conservation of momentum:

Proof (cont’d) Loss in K. E.

Proof (cont’d) • Since , loss of K. E. > 0 • There is always energy loss in an inelastic collision

Energy Changes in a Collision • Perfectly elastic collision • Proof

Proof Conservation of momentum: Law of restitution:

Proof (cont’d)

Special Cases of Elastic Collisions (a) Two equal masses in one direction – the second object moves off with the velocity, momentum and kinetic energy which the first has before the collision – the first object becomes stationary

Special Cases of Elastic Collisions (cont’d) • Two equal masses in two dimensions with m 2 stationary – the masses separate at 90 – e. g. particle collide with a nearly stationary helium nucleus

Special Cases of Elastic Collisions (cont’d) • Two unequal masses in two dimensions with m 2 stationary – m 1 > m 2: angle of separation < 90 – m 1 < m 2: angle of separation > 90

Special Cases of Elastic Collisions (cont’d) • A small object hitting a large object – the small mass keeps almost all the kinetic energy it possesses when it strikes the large object – e. g. an electron collides with a gas atom

Special Cases of Elastic Collisions (cont’d) • A large object hitting a small object – the motion of the large object is virtually unaffected while the small object sets off at twice the speed of the large object – e. g. a golf driver hits a golf ball

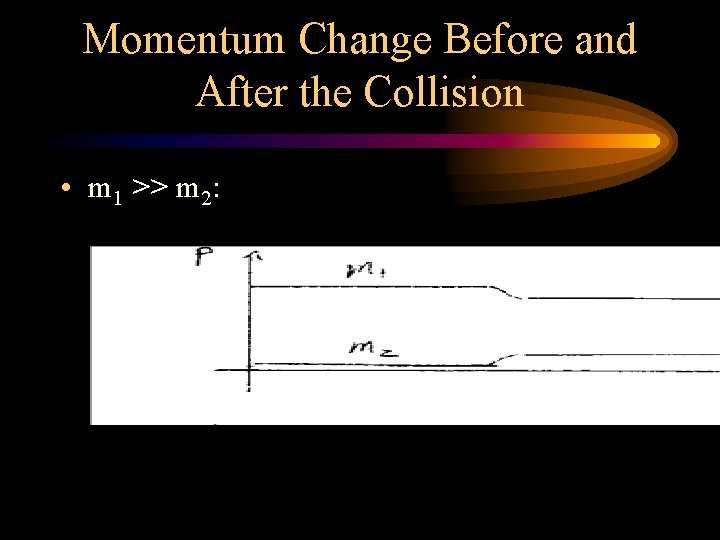
Momentum Change Before and After the Collision • m 1 >> m 2:

Momentum Change Before and After the Collision (cont’d) • m 1 = m 2:

Momentum Change Before and After the Collision (cont’d) • m 1 << m 2

Transfer of Kinetic Energy in an Elastic Collision

Transfer of Kinetic Energy in an Elastic Collision (cont’d) Where r = m 1/m 2

Transfer of Kinetic Energy in an Elastic Collision (cont’d) • r 0 f 0 • r 1 f 1

Explosive Separation of Two Masses initially At Rest • The K. E. of the two fragments are in the inverse ratio of their masses, i. e. the lighter part carries more kinetic energy

Explosive Separation of Two Masses initially At Rest (cont’d) • Recoil of cannons and rifles – cannon carries most of the released energy from the explosives • Alpha decay – most of the disintegration energy is carried by the lighter released -particle

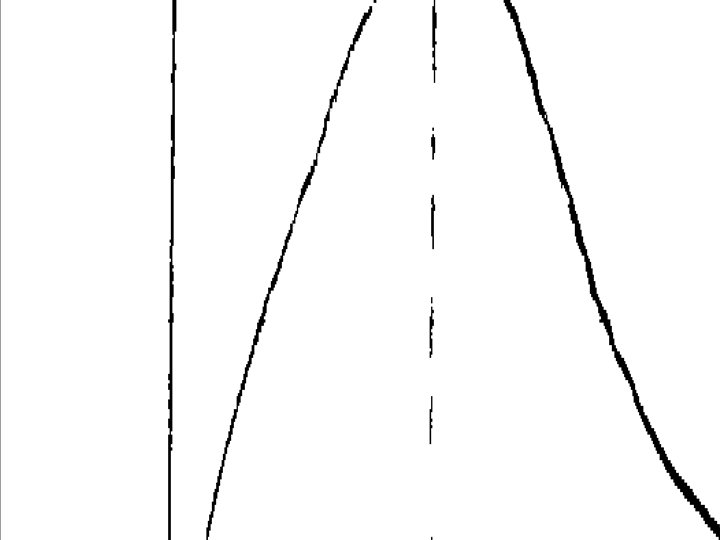
Collision Between Particles in a Cloud Chamber (1) • Cloud chamber filled with hydrogen – Collision between an particle and a Hnucleus – Angle of separation < 90° • Cloud chamber filled with helium gas – Collision between an particle and a helium nucleus – Angle of separation = 90°

Collision Between Particles in a Cloud Chamber (2) • Cloud chamber filled with oxygen – Collision between an particle and an Onucleus – Angle of separation > 90°

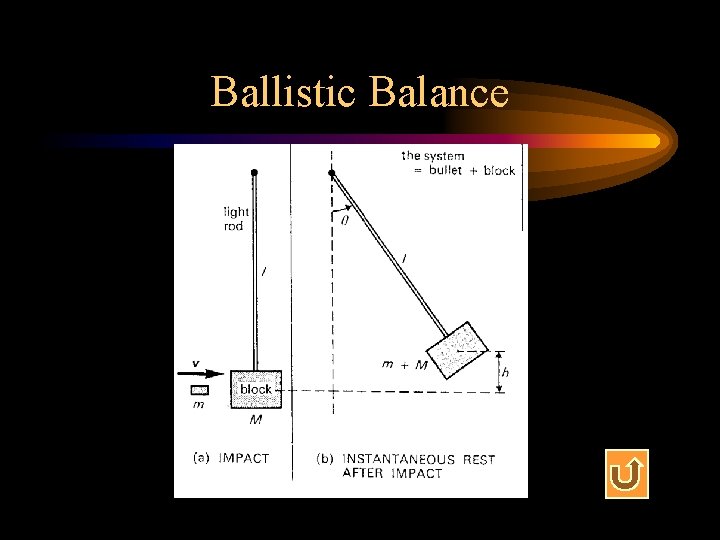
The Ballistic Balance (1) • The Impact – Mechanical energy is not conserved – Linear momentum is conserved in the horizontal direction Mv = (M + m)V

The Ballistic Balance (2) • The Swing – Mechanical energy is conserved – Momentum is not conserved

The Ballistic Balance (3) • Uses – To measure the speed of a bullet – To compare the inertial masses

Cloud Chamber Atom Tracks

Ballistic Balance