Linear Models for Classification Ch 4 34 5

Contents l 4. 3 Probabilistic Discriminative Models l 4. 4 The Laplace Approximation l

3 Approaches for classification ¨ Discriminant Functions ¨ Probabilistic Generative Models < Fit class-conditional

Fixed basis functions l Assume fixed nonlinear transformation ¨ Transform inputs using a vector

Logistic regression l Logistic regression model ¨ Posterior probability of a class for two-class

Logistic regression (Cont’d) l Determining the parameters using ML ¨ Likelihood function: ¨ Cross-entropy

Iterative reweighted least squares l Linear regression models in ch. 3 ¨ ML solution

Iterative reweighted least squares (Cont’d) l Sum-of-squares error function: ¨ Newton-Raphson update: l Cross-entropy

Multiclass logistic regerssion l Posterior probability for multiclassification l We can use ML to

Multiclass logistic regression (Cont’d) l The derivative of the error function ¨ Same form,

Probit regression l For a broad range of class-conditional distributions, described by the exponential

Probit regression l Noisy threshold model l Corresponding activation function when θ is drawn

Canonical link functions l We have seen that for some models, if we take

Canonical link functions (Cont’d) l Conditional distributions of the target variable ¨ Log likelihood:

The Laplace approximation We cannot integrate exactly over the parameter vector since the posterior

The Laplace approximation (Cont’d) l M-dimensional case (C) 2006, SNU Biointelligence Lab, http: //bi.

Model comparison and BIC l Laplace approximation to the normalization constant Z ¨ This

Bayesian Logistic Regression l Exact Bayesian inference is intractable. ¨ Gaussian prior: ¨ Posterior:

Predictive distribution l Can be obtained by marginalizing w. r. t the posterior distribution

Predictive distribution l Resulting variational approximation to the predictive distribution ¨ To integrate over

Slides: 20

Download presentation

Linear Models for Classification: Ch 4. 3~4. 5 Pattern Recognition and Machine Learning, C. M. Bishop, 2006. Summarized by Seung-Joon Yi Biointelligence Laboratory, Seoul National University http: //bi. snu. ac. kr/ 1

3 Approaches for classification ¨ Discriminant Functions ¨ Probabilistic Generative Models < Fit class-conditional densities and class priors separately < Apply Bayes’ theorem to find the posterior class probabilities < Posterior probability of a class can be written as – Logistic sigmoid acting on a linear function of x (2 classes) – Softmax transformation of a linear function of x (Multiclass) < The parameters of the densities as well as the class priors can be determined using Maximum Likelihood ¨ Probabilistic Discriminative Models < Use the functional form of the generalized linear model explicitly < Determine the parameters directly using Maximum Likelihood (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 3

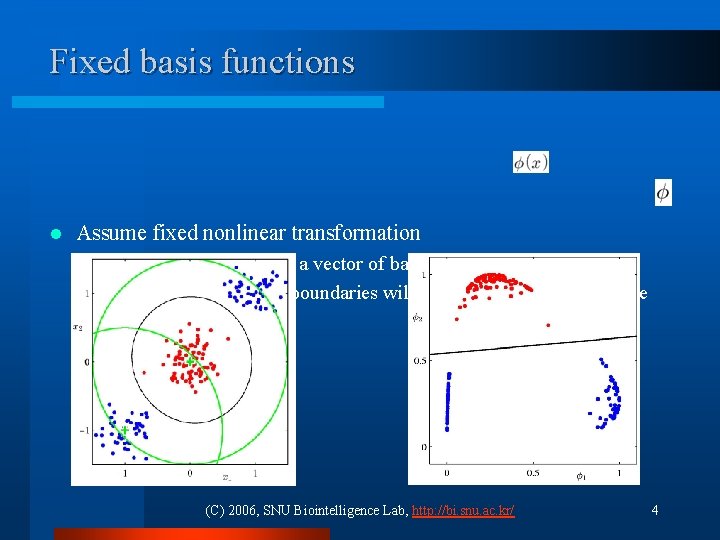
Fixed basis functions l Assume fixed nonlinear transformation ¨ Transform inputs using a vector of basis functions ¨ The resulting decision boundaries will be linear in the feature space (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 4

Logistic regression l Logistic regression model ¨ Posterior probability of a class for two-class problem: l The number of adjustable parameters (M-dimensional, 2 -class) ¨ 2 Gaussian class conditional densities (generative model) < 2 M parameters for means < M(M+1)/2 parameters for (shared) covariance matrix < Grows quadratically with M ¨ Logistic regression (discriminative model) < M parameters for < Grows linearly with M (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 5

Logistic regression (Cont’d) l Determining the parameters using ML ¨ Likelihood function: ¨ Cross-entropy error function (negative log likelihood) ¨ The gradient of the error function w. r. t. w (the same form as the linear regression model) (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 6

Iterative reweighted least squares l Linear regression models in ch. 3 ¨ ML solution on the assumption of a Gaussian noise leads to a close-form solution, as a consequence of the quadratic dependence of the log likelihood on the parameter w. l Logistic regression model ¨ No longer a closed-form solution ¨ But the error function is concave and has a unique minimum < Efficient iterative technique can be used < The Newton-Raphson update to minimize a function E(w) – Where H is the Hessian matrix, the second derivatives of E(w) (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 7

Iterative reweighted least squares (Cont’d) l Sum-of-squares error function: ¨ Newton-Raphson update: l Cross-entropy error function: ¨ Newton-Rhapson update: (iterative reweighted least squares) (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 8

Multiclass logistic regerssion l Posterior probability for multiclassification l We can use ML to determine the parameters directly. ¨ Likelihood function using 1 -of-K coding scheme ¨ Cross-entropy error function for the multiclassification (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 9

Multiclass logistic regression (Cont’d) l The derivative of the error function ¨ Same form, the product of error times the basis function. l The Hessian matrix ¨ IRLS algorithm can also be used for a batch processing (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 10

Probit regression l For a broad range of class-conditional distributions, described by the exponential family, the resulting posterior class probabilities are given by a logistic(or softmax) transformation acting on a linear function of the feature variables. ¨ However this is not the case for all choices of class-conditional density ¨ It might be worth exploring other types of discriminative probabilistic model (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 11

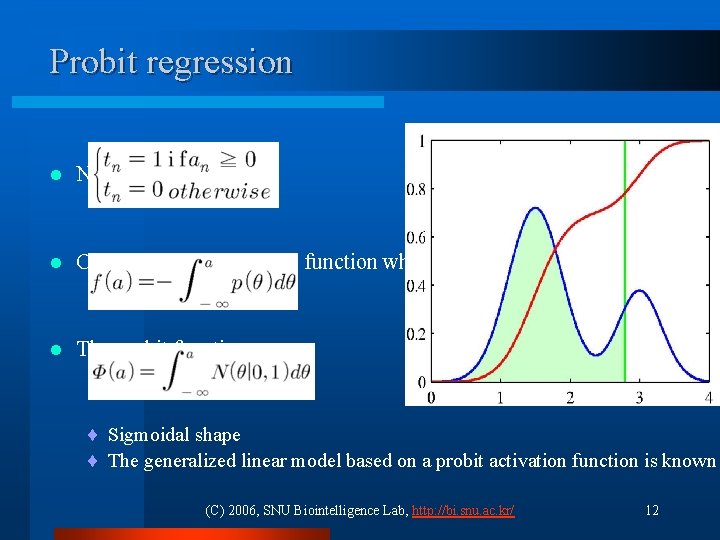
Probit regression l Noisy threshold model l Corresponding activation function when θ is drawn from p(θ) l The probit function ¨ Sigmoidal shape ¨ The generalized linear model based on a probit activation function is known (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 12

Canonical link functions l We have seen that for some models, if we take the derivative of the error ¨ Logistic regression model with sigmoid activation function ¨ Logistic regression model with softmax activation function l This is a general result of assuming a conditional distribution for the target variab (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 13

Canonical link functions (Cont’d) l Conditional distributions of the target variable ¨ Log likelihood: ¨ The derivative of the log likelihood: where l The canonical link function: then (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 14

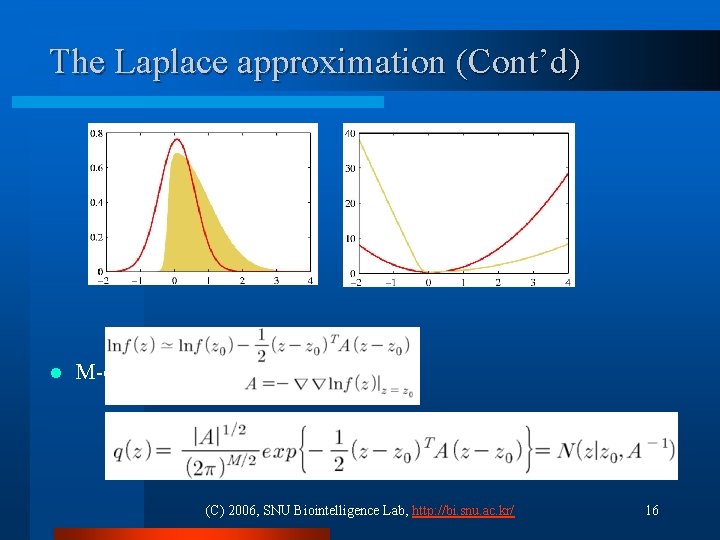
The Laplace approximation We cannot integrate exactly over the parameter vector since the posterior l The Laplace approximation: find a Gaussian approximation centered on t l ¨ Taylor expansion of the logarithm of the target function: ¨ Resulting approximated Gaussian distribution: (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 15

Model comparison and BIC l Laplace approximation to the normalization constant Z ¨ This result can be used to obtain an approximation to the model evidence, wh l Consider a set of models having parameters ¨ The log of model evidence can be approximated as ¨ Further approximation with some more assumption: Bayesian Information Criterion (BIC) (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 17

Bayesian Logistic Regression l Exact Bayesian inference is intractable. ¨ Gaussian prior: ¨ Posterior: ¨ Log of posterior: l Laplace approximation of posterior distribution (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 18

Predictive distribution l Can be obtained by marginalizing w. r. t the posterior distribution p (w|t) w where l a is a marginal distribution of a Gaussian which is also Gaussian (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 19

Predictive distribution l Resulting variational approximation to the predictive distribution ¨ To integrate over a, we make use of the close similarity between the logistic Then where ¨ Finally we get (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 20