Linear Matrix Inequalities in System and Control Theory

Linear Matrix Inequalities in System and Control Theory Solmaz Sajjadi Kia Adviser: Prof. Jabbari System, Dynamics and Control Seminar UCI, MAE Dept. April 14, 2008

Linear Matrix Inequality (LMI) ØSet of n polynomial inequalities in x, e. g. , ØConvex constraint on x

Matrices as Variable Multiple LMIs

LMI Problems Feasibility Minimization Problem

How do we cast our control problems in LMI form? We rely on quadratic function V(x)=x’Px Three Useful Properties to Cast Problems in Convex LMI From ØCongruent Transformation ØS-Procedure ØSchur Complement

Congruent transformation

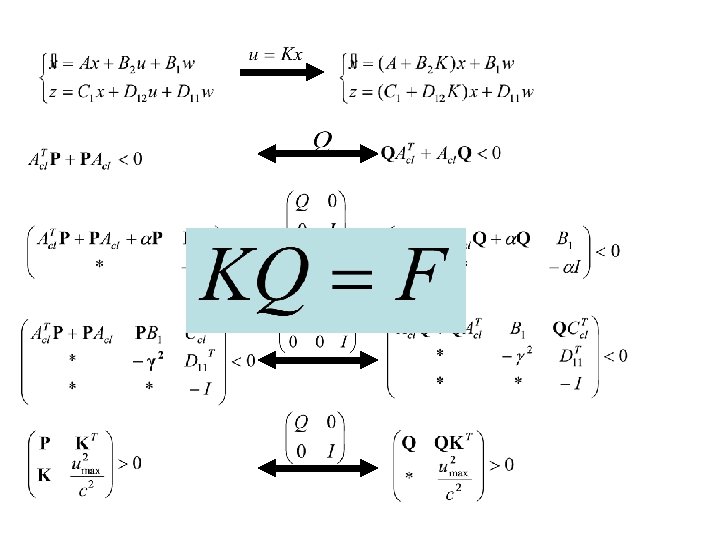
Stable State Feedback Synthesis Problem

S Procedure Three Useful Properties to Cast Problems in Convex LMI From ØCongruent Transformation ØS-Procedure ØSchur Complement

Reachable Set/Invariant Set for Peak Bound Disturbance ØThe reachable set (from zero): is the set of points the state vector can reach with zero initial condition, given some limitations on the disturbance. ØThe invariant set: is the set that the state vector does not leave once it is inside of it, again given some limits on the disturbance.

Reachable Set/Invariant Set for Peak Bound Disturbance Ellipsoidal Estimate Peak Bound Disturbance

Three Useful Properties to Cast Problems in Convex LMI From Linear (thus convex) Verses Nonlinear Convex inequality Nonlinear (convex) inequalities are converted to LMI form using Schur Complement ØCongruent Transformation ØS-Procedure ØSchur Complement

H∞ or L 2 Gain

Norm of a vector in an ellipsoid Find Max of ||u||=||Kx|| for x in {x| x. TPx≤c 2 }

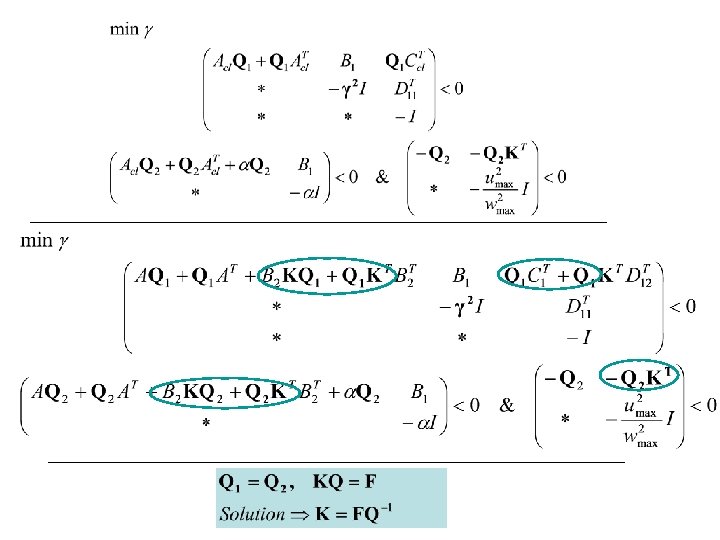
A Saturation Problem: Synthesis/Analysis of a Bounded State Feedback Controller (||u||<umax) exposed w. T(t)w(t)≤w 2 max ØAnalysis: What is the largest disturbance this system can tolerate with K ØSynthesis: Find a K such that controller never saturates

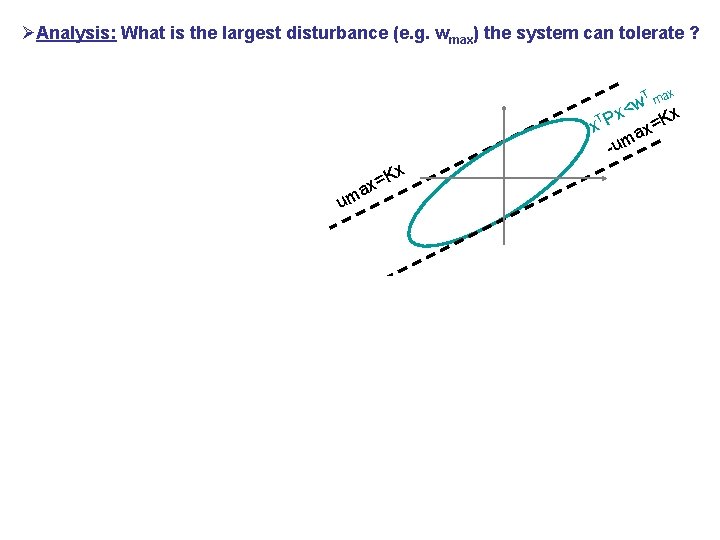
ØAnalysis: What is the largest disturbance (e. g. wmax) the system can tolerate ? T ax w m < x x x. T P ax=K -um x um a K x=

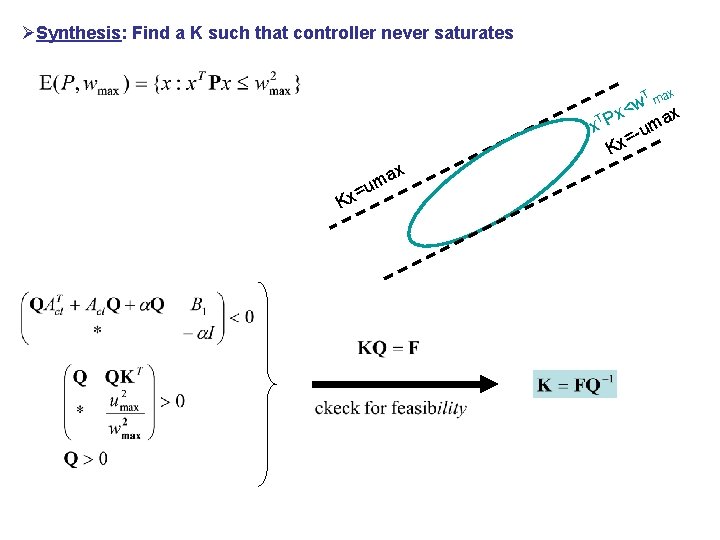
ØSynthesis: Find a K such that controller never saturates T ax w m < x x x. T P -uma = Kx x K ma u x=

Good Reference ØProf. Jabbari’s Note on LMIs ØS. Boyd, L. El Ghaoui, E. Feron, V. Balakrishnan, “Linear Matrix Inequalities in Systems and Control Theory”