Linear Interpolation Applying weighted averages to some graphics

Linear Interpolation Applying “weighted averages” to some graphics problems: animations and curve-drawing

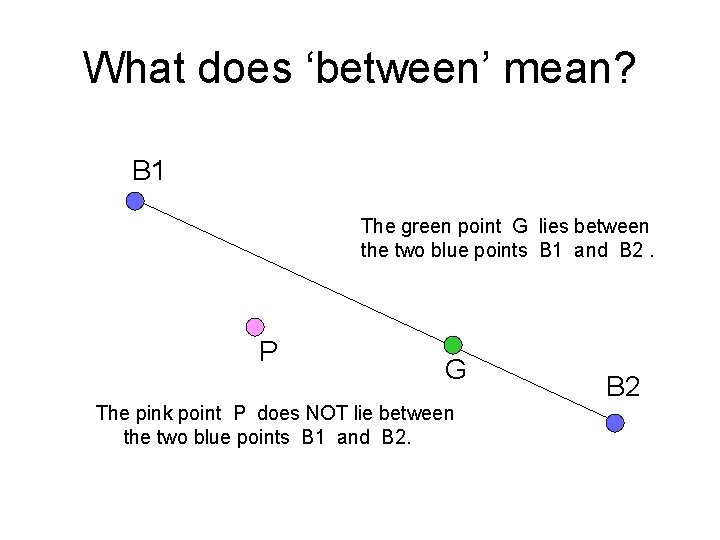
What does ‘between’ mean? B 1 The green point G lies between the two blue points B 1 and B 2. P G The pink point P does NOT lie between the two blue points B 1 and B 2

Using a “weighted average” • Suppose (x 1, y 1) and (x 2, y 2) are points • The point located half-way in-between is: midpoint = (½)(x 1, y 1) + (½)(x 2, y 2) • It’s the “average” of (x 1, y 1) and (x 2, y 2) • Here’s another point on the line-segment that lies between (x 1, y 1) and (x 2, y 2): (x’, y’) = (¼)(x 1, y 1) + (¾)(x 2, y 2) • It’s a “weighted average” of the endpoints

The generalization • Let B 1 = (x 1, y 1) and B 2 = (x 2, y 2) be the two endpoints of a line-segment. Suppose w 1 and w 2 are “weights” (i. e. , neither is negative, and their sum equals 1). Then the point P = w 1*B 1 + w 2*B 2 is called a “weighted average” of B 1 and B 2 , and P will be located “in-between” B 1 and B 2. • Here P is obtained by “linear interpolation”

Describing a line-segment • Mathematical description of line-segments • Let B 1 = (x 1, y 1) and B 2 = (x 2, y 2) be the two end-points of a given line-segment • Let t be a real number whose value can vary continuously, from 0. 0 to 1. 0 • Then point P = (1 -t)*B 1 + t*B 2 will vary continuously over the entire line-segment, starting at B 1 (when t=0. 0) and ending up at B 2 (when t=1. 0)

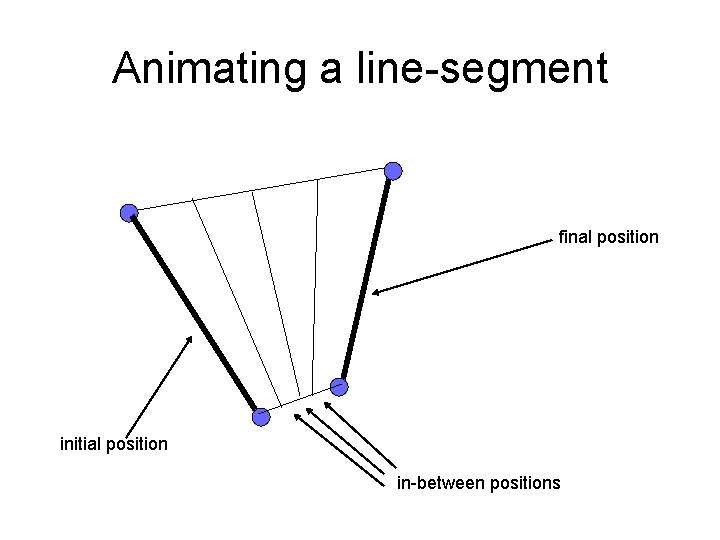
Animating a line-segment final position initial position in-between positions

The programming idea • We only need to specify the segment’s two endpoints at the start and the finish • As the segment moves all its intermediate endpoint locations are then calculated as linear interpolations (“weighted averages”) • This idea can be simultaneously applied to lots of different line-segments (e. g. , to all the sides of a polygon, or to all the “edges” in a wire-frame model)

The ‘polyline’ structure typedef struct { float x, y; } point_t; typedef struct { int numverts; point_t vert[ MAXVERT ]; } polyline_t; // declare two polylines (for start and finish) // and a variable polyline (for “in-betweens”) tween[i]. x = (1 -t)*B 1[i]. x + t*B 2[i]. x; tween[i]. y = (1 -t)*B 1[i]. y + t*B 2[i]. y;

The ‘tweening. cpp’ demo • We illustrate this idea for animating simple polygons, using random-numbers for the coordinates of the starting vertices and the ending vertices • We use linear interpolation to calculate the sequence of the “in-between” vertices • We use Bresenham’s line-drawing method to “connect-the-dots” at each stage

Stick man

Drawing curves • Another application of “linear interpolation” • We can construct a so-called Bezier curve • The curve is determined by specifying a small number of “control points” • A recursive algorithm is then applied, to generate locations along a smooth curve • This idea is ‘de. Casteljau’s algorithm’ • Kai Long has written an implementation

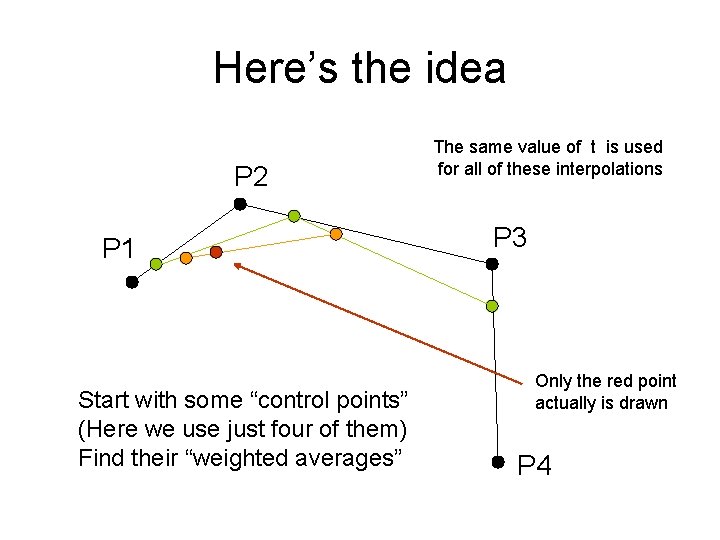
Here’s the idea P 2 P 1 Start with some “control points” (Here we use just four of them) Find their “weighted averages” The same value of t is used for all of these interpolations P 3 Only the red point actually is drawn P 4

Kai’s Implementation typedef struct { double h, v; } Point; typedef struct { int numcpts; Point cpts[ MAXVERT ]; } Bezier. Cruve; // helper function void middle( Point p, Point q, Point &mid ) { mid. x = (p. x + q. x)/2; mid. y = (p. y + q. y)/2; }

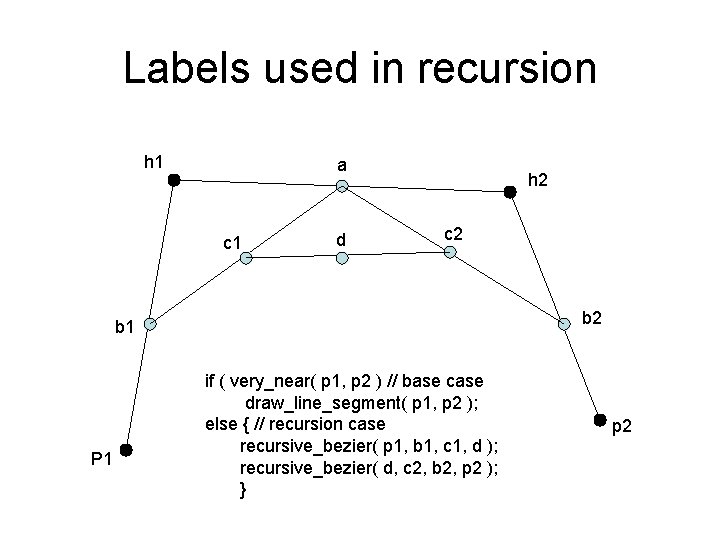
Labels used in recursion h 1 a c 1 d h 2 c 2 b 1 P 1 if ( very_near( p 1, p 2 ) // base case draw_line_segment( p 1, p 2 ); else { // recursion case recursive_bezier( p 1, b 1, c 1, d ); recursive_bezier( d, c 2, b 2, p 2 ); } p 2

In-class exercise • • Can you combine these two applications? Create a bezier curve with 4 control-points Create another one with 4 control-points Construct some in-between Bezier curves by applying linear-interpolation to pairs of corresponding control-points • So first curve will “morph” into second one