Linear Grammars with at most one variable at

Linear Grammars with at most one variable at the right side of a production Examples: Fall 2003 Costas Busch - RPI 1

A Non-Linear Grammar Number of Fall 2003 : in string Costas Busch - RPI 2

Another Linear Grammar Fall 2003 : Costas Busch - RPI 3

Right-Linear Grammars All productions have form: or Example: Fall 2003 string of terminals Costas Busch - RPI 4

Left-Linear Grammars All productions have form: or Example: Fall 2003 string of terminals Costas Busch - RPI 5

Regular Grammars Fall 2003 Costas Busch - RPI 6

Regular Grammars A regular grammar is any right-linear or left-linear grammar Examples: Fall 2003 Costas Busch - RPI 7

Observation Regular grammars generate regular languages Examples: Fall 2003 Costas Busch - RPI 8

Regular Grammars Generate Regular Languages Fall 2003 Costas Busch - RPI 9

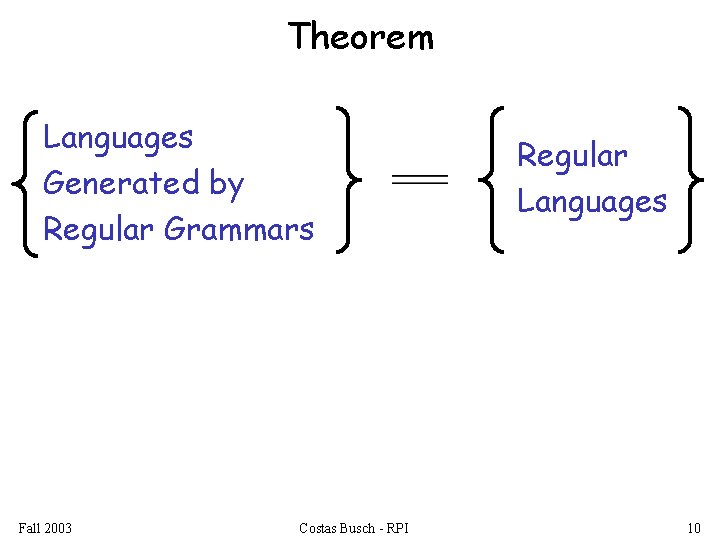
Theorem Languages Generated by Regular Grammars Fall 2003 Costas Busch - RPI Regular Languages 10

Theorem - Part 1 Languages Generated by Regular Grammars Regular Languages Any regular grammar generates a regular language Fall 2003 Costas Busch - RPI 11

Theorem - Part 2 Languages Generated by Regular Grammars Regular Languages Any regular language is generated by a regular grammar Fall 2003 Costas Busch - RPI 12

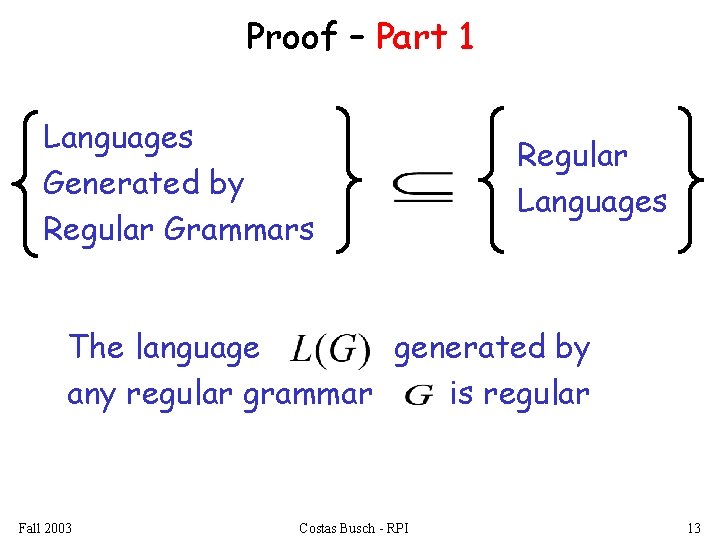
Proof – Part 1 Languages Generated by Regular Grammars Regular Languages The language generated by any regular grammar is regular Fall 2003 Costas Busch - RPI 13

The case of Right-Linear Grammars Let be a right-linear grammar We will prove: Proof idea: Fall 2003 is regular We will construct NFA with Costas Busch - RPI 14

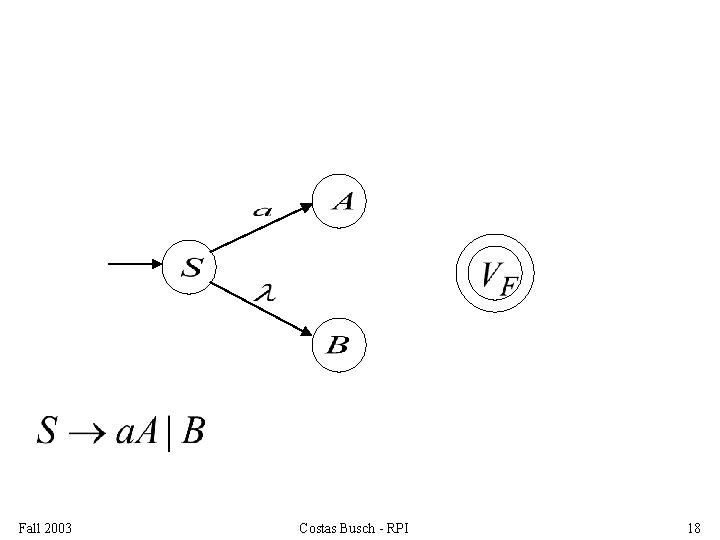
Grammar is right-linear Example: Fall 2003 Costas Busch - RPI 15

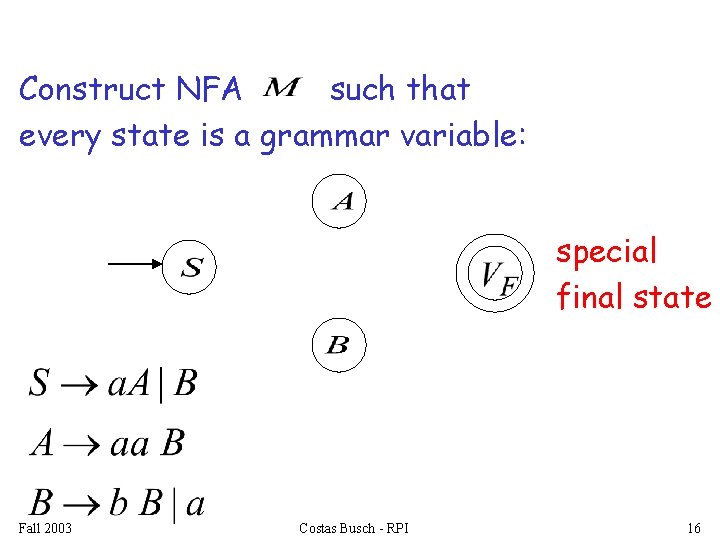
Construct NFA such that every state is a grammar variable: special final state Fall 2003 Costas Busch - RPI 16

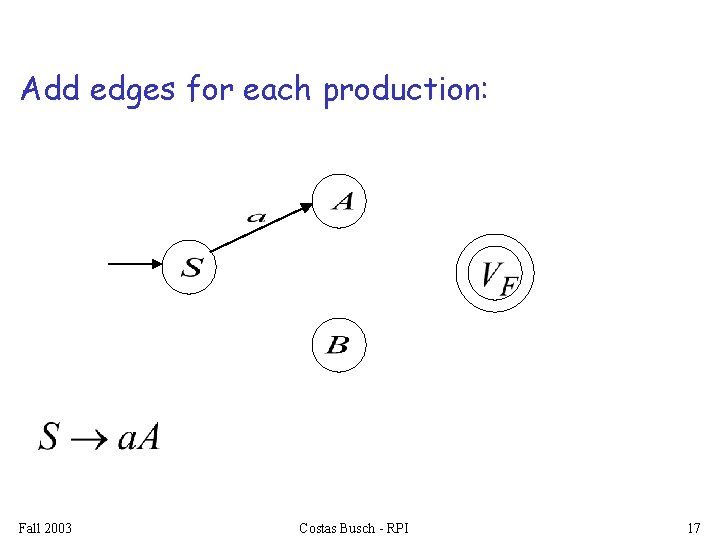
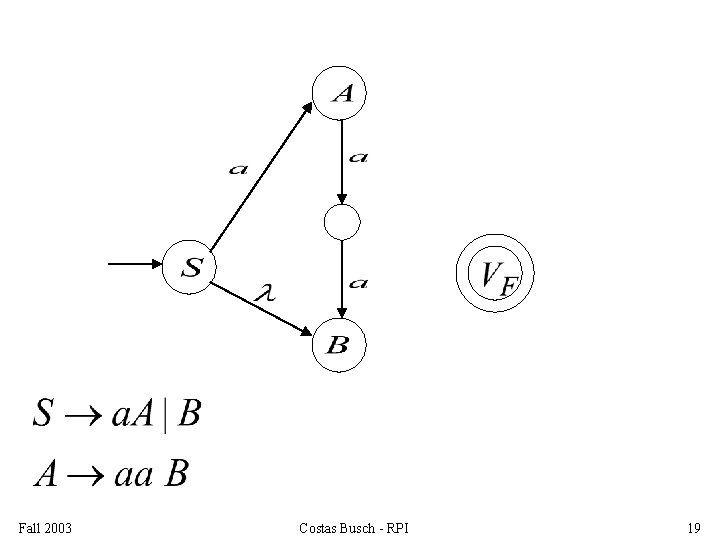
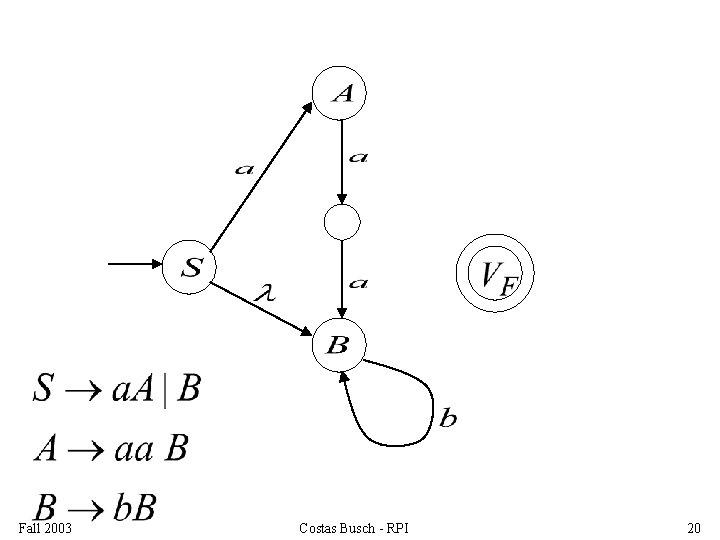
Add edges for each production: Fall 2003 Costas Busch - RPI 17

Fall 2003 Costas Busch - RPI 18

Fall 2003 Costas Busch - RPI 19

Fall 2003 Costas Busch - RPI 20

Fall 2003 Costas Busch - RPI 21

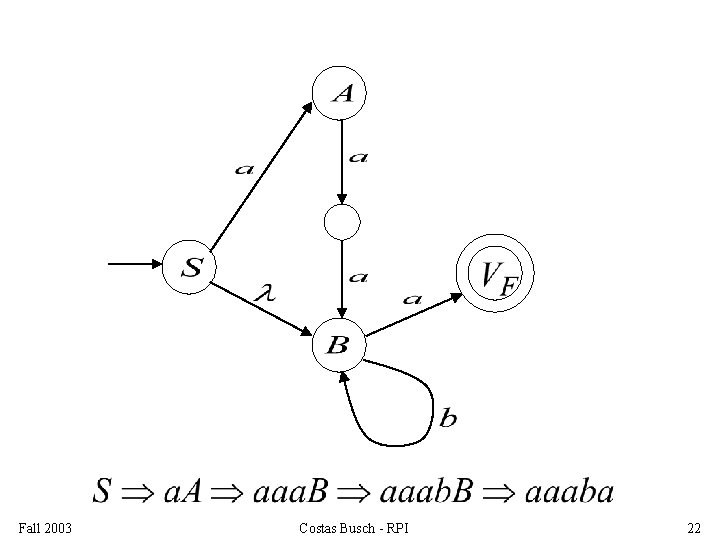
Fall 2003 Costas Busch - RPI 22

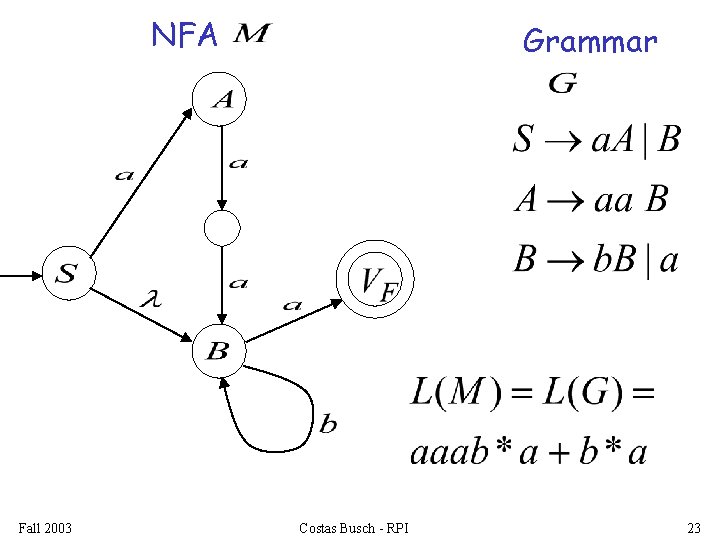
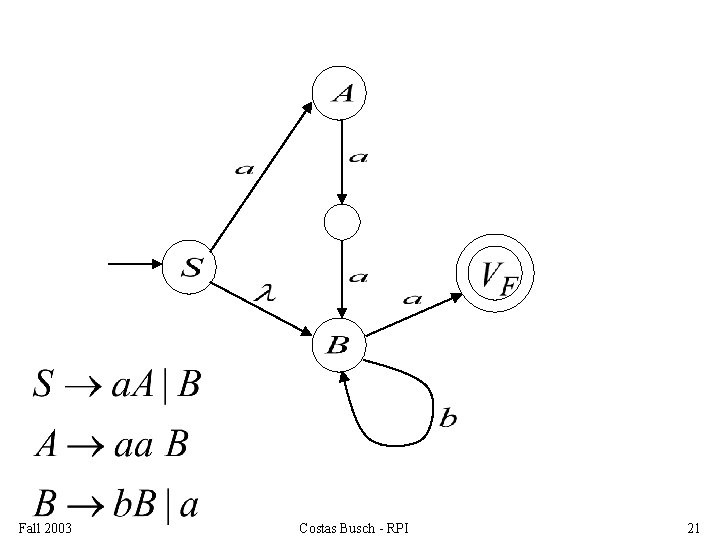
NFA Fall 2003 Grammar Costas Busch - RPI 23

In General A right-linear grammar has variables: and productions: or Fall 2003 Costas Busch - RPI 24

We construct the NFA each variable such that: corresponds to a node: special final state Fall 2003 Costas Busch - RPI 25

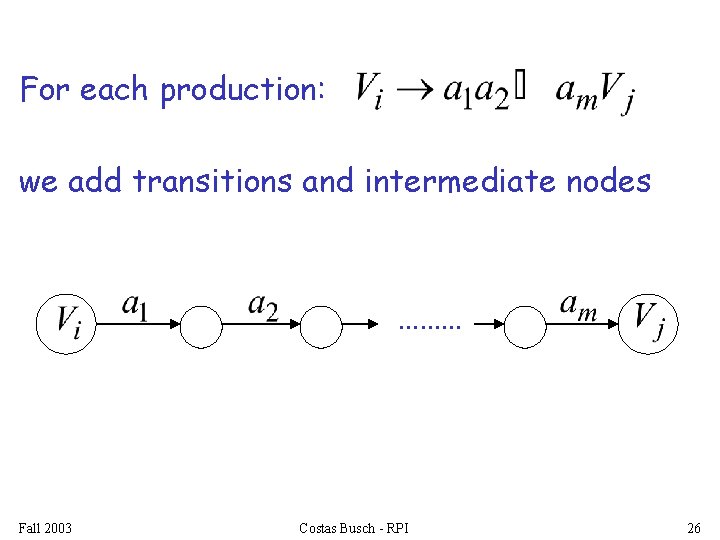
For each production: we add transitions and intermediate nodes ……… Fall 2003 Costas Busch - RPI 26

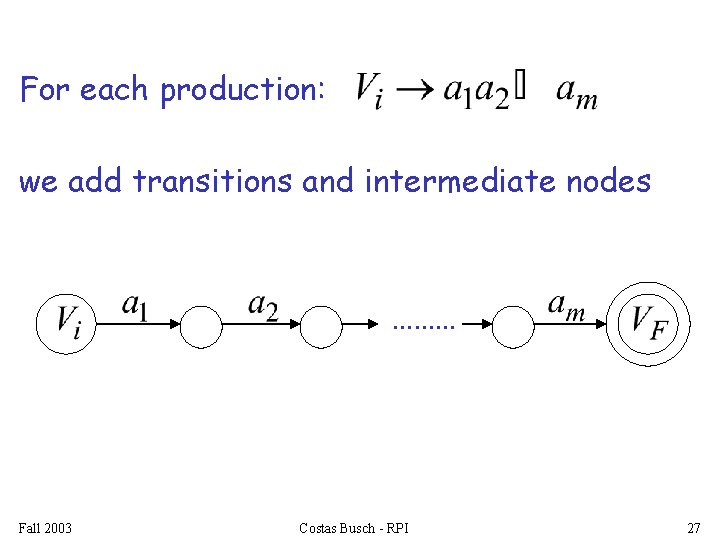
For each production: we add transitions and intermediate nodes ……… Fall 2003 Costas Busch - RPI 27

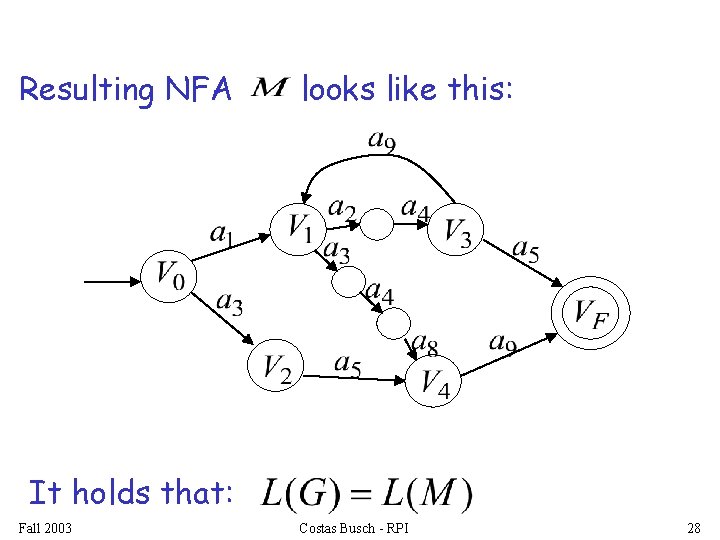
Resulting NFA looks like this: It holds that: Fall 2003 Costas Busch - RPI 28

The case of Left-Linear Grammars Let be a left-linear grammar We will prove: is regular Proof idea: We will construct a right-linear grammar with Fall 2003 Costas Busch - RPI 29

Since is left-linear grammar the productions look like: Fall 2003 Costas Busch - RPI 30

Construct right-linear grammar Left linear Right linear Fall 2003 Costas Busch - RPI 31

Construct right-linear grammar Left linear Right linear Fall 2003 Costas Busch - RPI 32

It is easy to see that: Since Regular Language Fall 2003 is right-linear, we have: Regular Language Costas Busch - RPI Regular Language 33

Proof - Part 2 Languages Generated by Regular Grammars Regular Languages Any regular language is generated by some regular grammar Fall 2003 Costas Busch - RPI 34

Any regular language is generated by some regular grammar Proof idea: Let be the NFA with Construct from such that Fall 2003 . a regular grammar Costas Busch - RPI 35

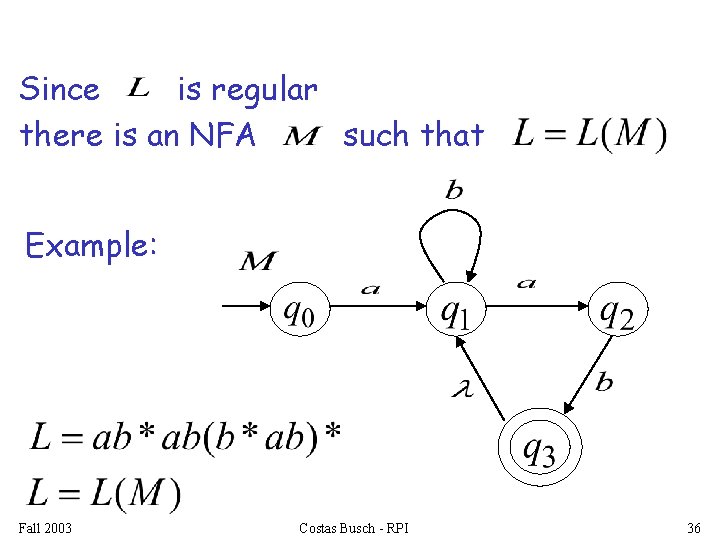
Since is regular there is an NFA such that Example: Fall 2003 Costas Busch - RPI 36

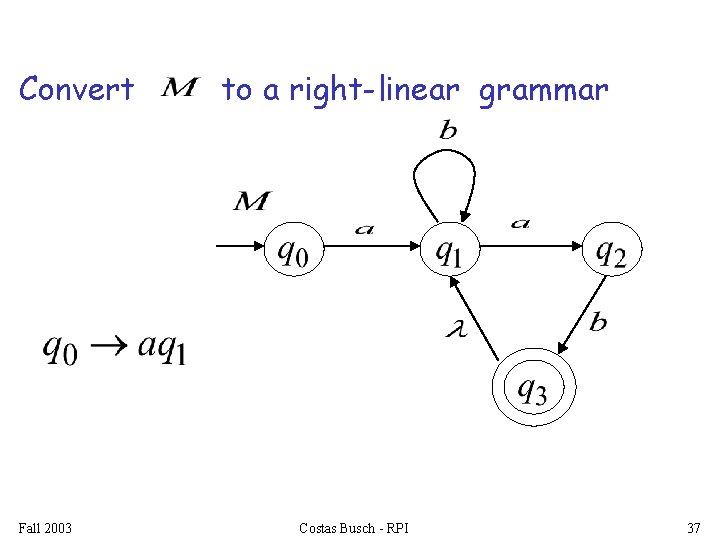
Convert Fall 2003 to a right-linear grammar Costas Busch - RPI 37

Fall 2003 Costas Busch - RPI 38

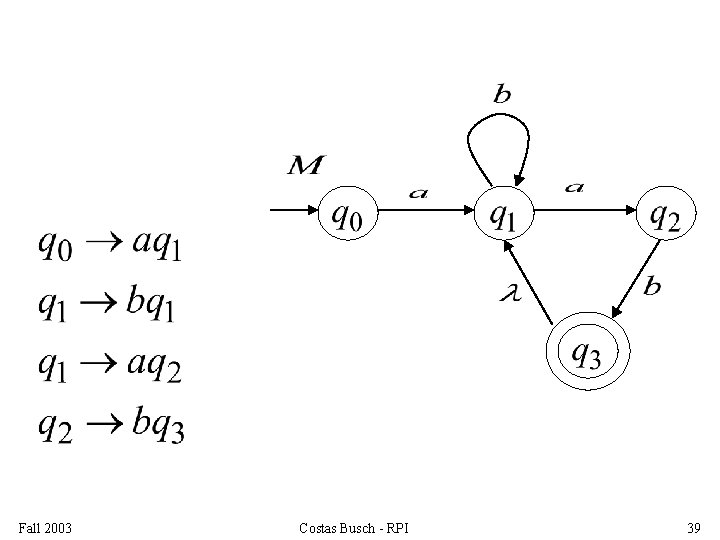
Fall 2003 Costas Busch - RPI 39

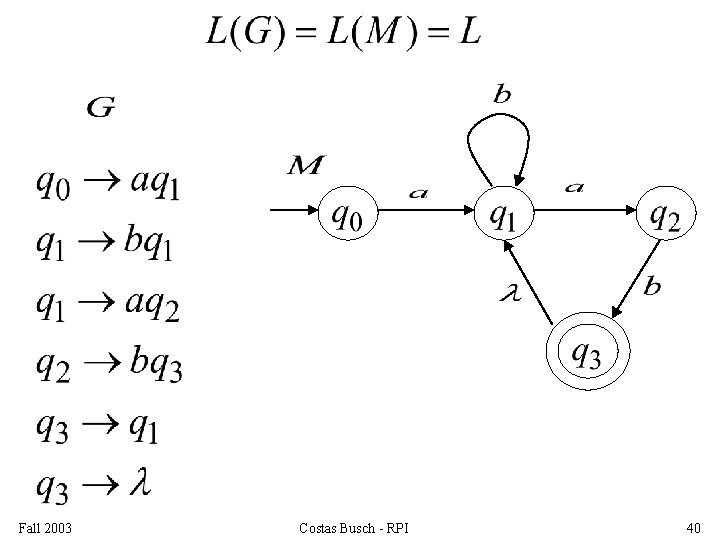
Fall 2003 Costas Busch - RPI 40

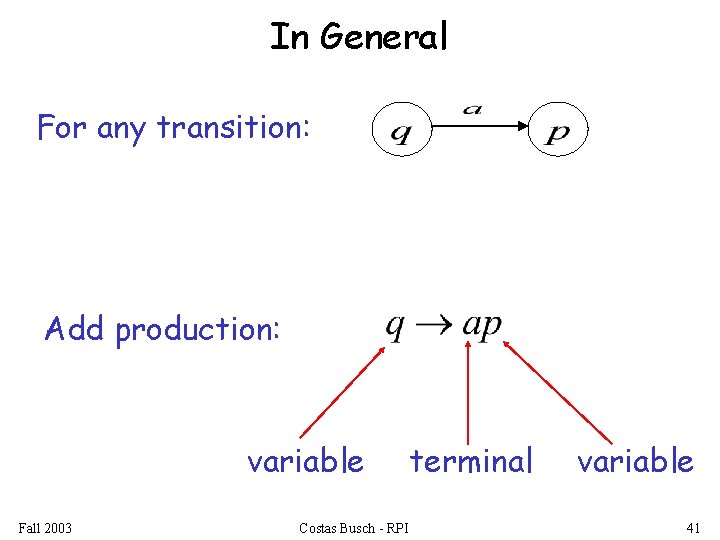
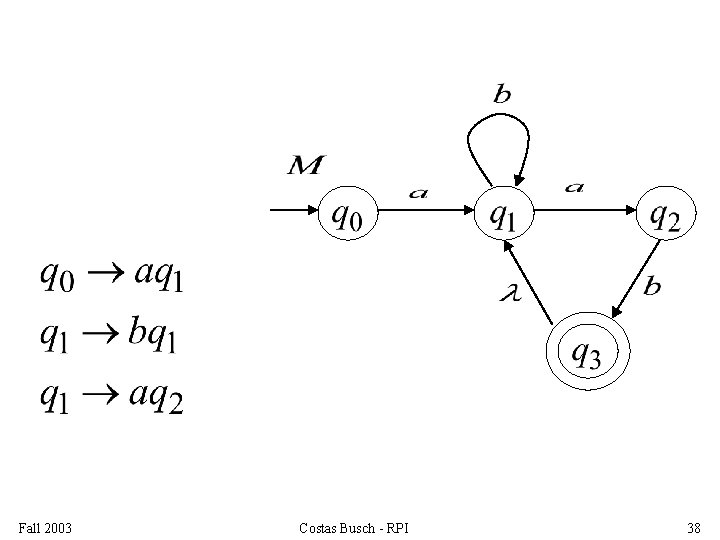
In General For any transition: Add production: variable Fall 2003 Costas Busch - RPI terminal variable 41

For any final state: Add production: Fall 2003 Costas Busch - RPI 42

Since is right-linear grammar is also a regular grammar with Fall 2003 Costas Busch - RPI 43