Linear Functions Review of plotting points Graphing lines

Linear Functions § § § § Review of plotting points Graphing lines by plotting points Interpreting and finding the slope of a line X- and y- intercepts Graphing from slope-intercept form Graphing from point-slope form Finding the equation of a line

Warm-up One morning a Buddhist monk sets out at sunrise to climb a path up the mountain to reach the temple at the summit. He arrives at the temple just before sunset. A few days later he leaves the temple at sunrise to descend the mountain, travelling a little faster. Was the monk ever at the same spot at the same time on both days? Explain.

Homework?

Goals for today 1. Review graphing of linear functions 2. Go over classroom expectations and procedures

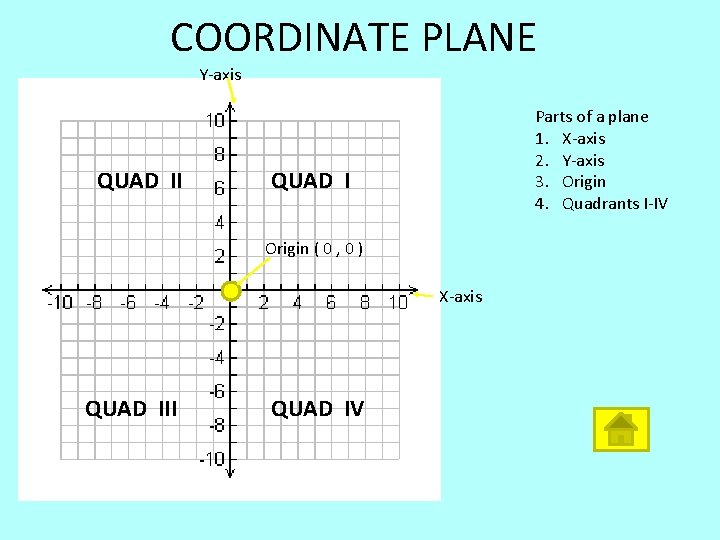
COORDINATE PLANE Y-axis QUAD II Parts of a plane 1. X-axis 2. Y-axis 3. Origin 4. Quadrants I-IV QUAD I Origin ( 0 , 0 ) X-axis QUAD III QUAD IV

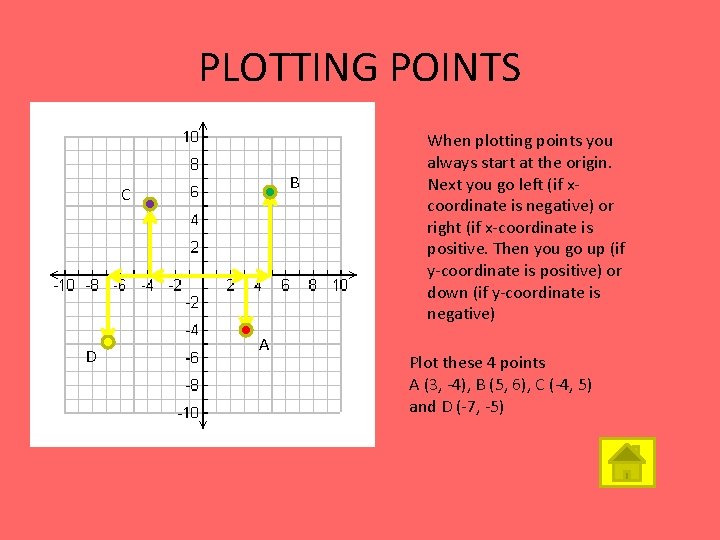
PLOTTING POINTS B C D A When plotting points you always start at the origin. Next you go left (if xcoordinate is negative) or right (if x-coordinate is positive. Then you go up (if y-coordinate is positive) or down (if y-coordinate is negative) Plot these 4 points A (3, -4), B (5, 6), C (-4, 5) and D (-7, -5)

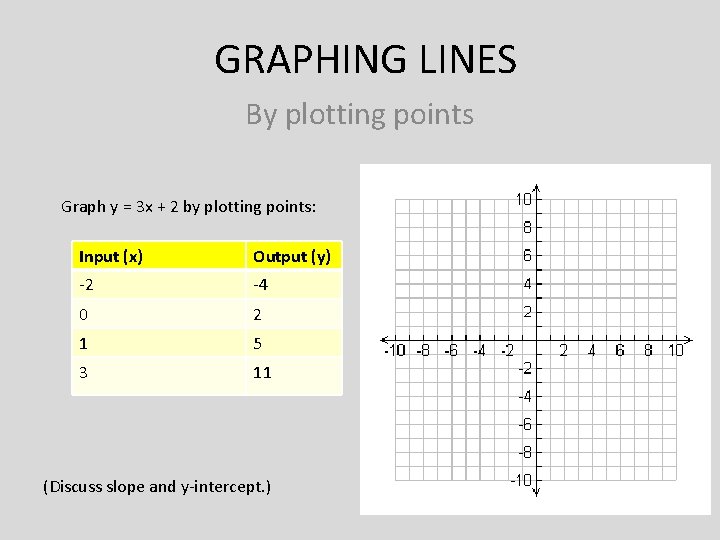
GRAPHING LINES By plotting points Graph y = 3 x + 2 by plotting points: Input (x) Output (y) -2 -4 0 2 1 5 3 11 (Discuss slope and y-intercept. )

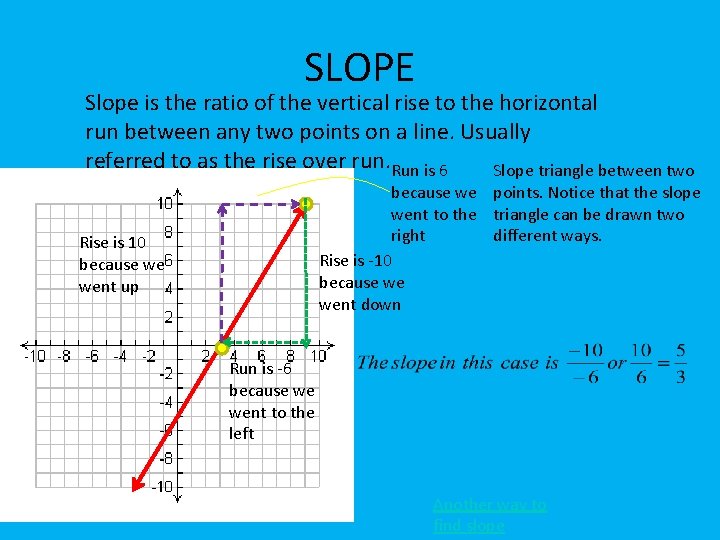
SLOPE Slope is the ratio of the vertical rise to the horizontal run between any two points on a line. Usually referred to as the rise over run. Run is 6 Slope triangle between two because we points. Notice that the slope went to the triangle can be drawn two right different ways. Rise is -10 because we went down Rise is 10 because we went up Run is -6 because we went to the left Another way to find slope

FORMULA FOR FINDING SLOPE

Find the slope of the line between the two points (-3, 8) and (10, -4) If it helps label the points. Then use the formula EXAMPLES Find the slope of the line that passes through the points (2, -4) and (5, 1).

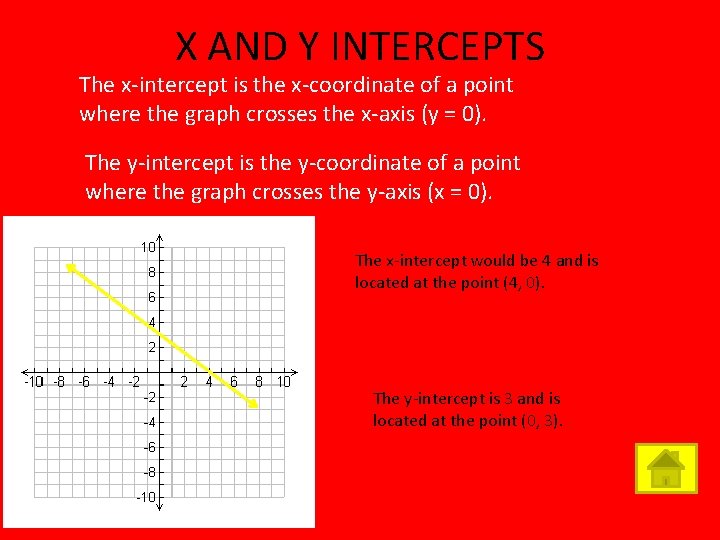
X AND Y INTERCEPTS The x-intercept is the x-coordinate of a point where the graph crosses the x-axis (y = 0). The y-intercept is the y-coordinate of a point where the graph crosses the y-axis (x = 0). The x-intercept would be 4 and is located at the point (4, 0). The y-intercept is 3 and is located at the point (0, 3).

Find the x- and y-intercepts: Y = 2 x – 5 3 x + 4 y = 12 2 x = y + 6 Y = 1/2 x + 4 Y = 3 x - 1 What do you notice about the y-intercept of lines in y = mx + b form?

SLOPE-INTERCEPT FORM OF A LINE Y = mx + b m b slope y - intercept If a line is not in slope-intercept form, then we must solve for “y” to get it there.

IN SLOPE-INTERCEPT NOT IN SLOPE-INTERCEPT y = 3 x – 5 y – x = 10 y = -2 x + 10 2 y – 8 = 6 x y = -. 5 x – 2 y + 4 = 2 x Put y – x = 10 into slope-intercept form Add x to both sides and would get y = x + 10 Put 2 y – 8 = 6 x into slope-intercept form. Add 8 to both sides then divide by 2 and would get y = 3 x + 4 Put y + 4 = 2 x into slope-intercept form. Subtract 4 from both sides and would get y = 2 x – 4. EXAMPLES

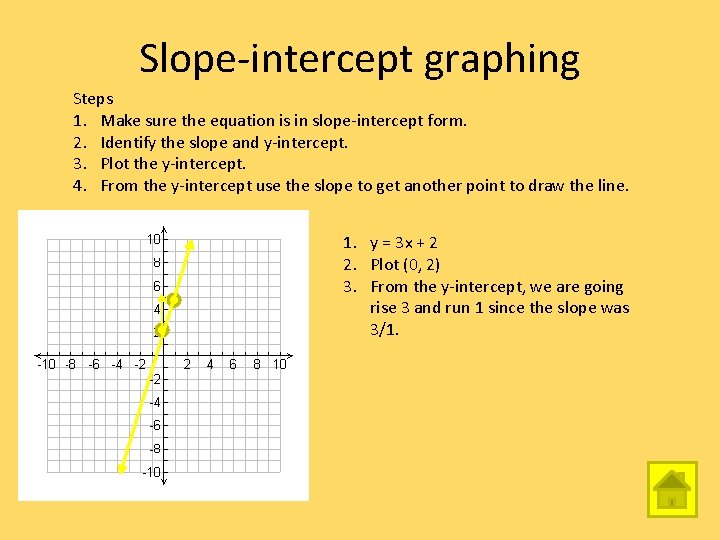
Slope-intercept graphing Steps 1. Make sure the equation is in slope-intercept form. 2. Identify the slope and y-intercept. 3. Plot the y-intercept. 4. From the y-intercept use the slope to get another point to draw the line. 1. y = 3 x + 2 2. Plot (0, 2) 3. From the y-intercept, we are going rise 3 and run 1 since the slope was 3/1.

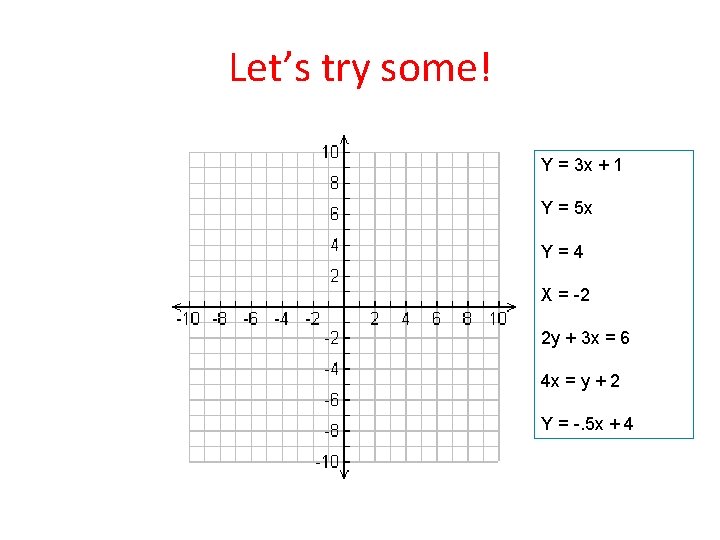
Let’s try some! Y = 3 x + 1 Y = 5 x Y=4 X = -2 2 y + 3 x = 6 4 x = y + 2 Y = -. 5 x + 4

Warm-up: 3 x – 5 y = 15 Find the x-intercept. Find the y-intercept. Find the slope. Write in slope-intercept form. Graph.

desmos

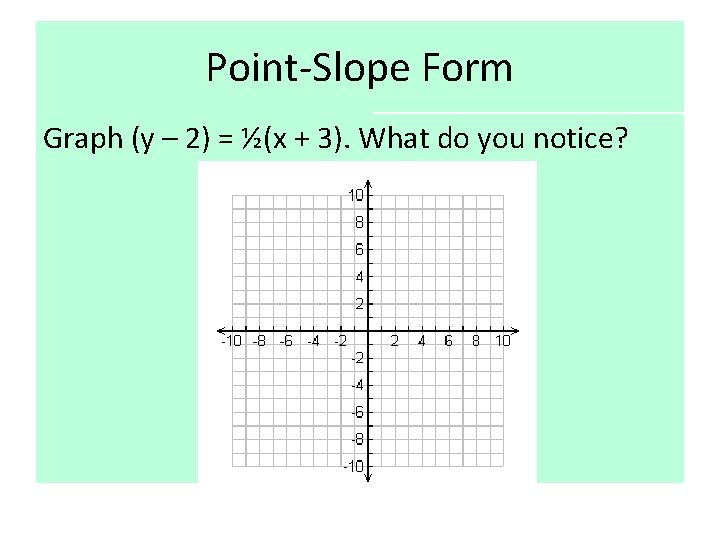
Point-Slope Form Graph 3). What do you notice? Graph (y (y –– 2) 2) == ½ ½(x(x++3). What do you notice?

Point-Slope Form •

Let’s try some.

In Summary

BEFORE: equation NOW: graph equation

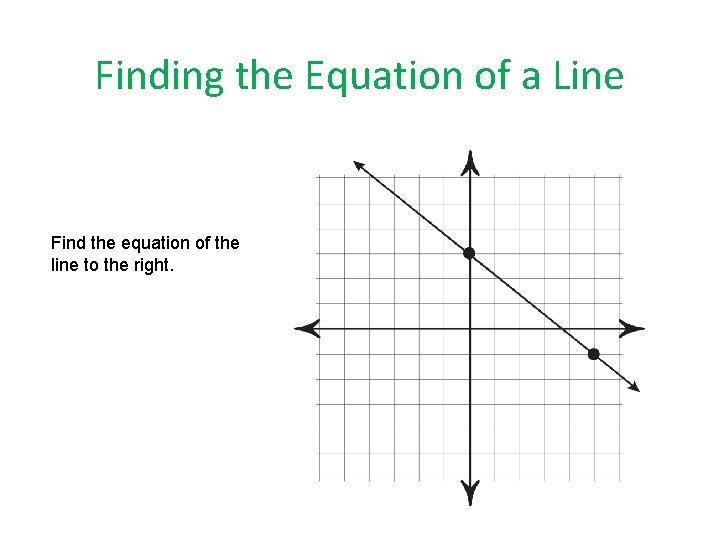
Finding the Equation of a Line Find the equation of the line to the right.

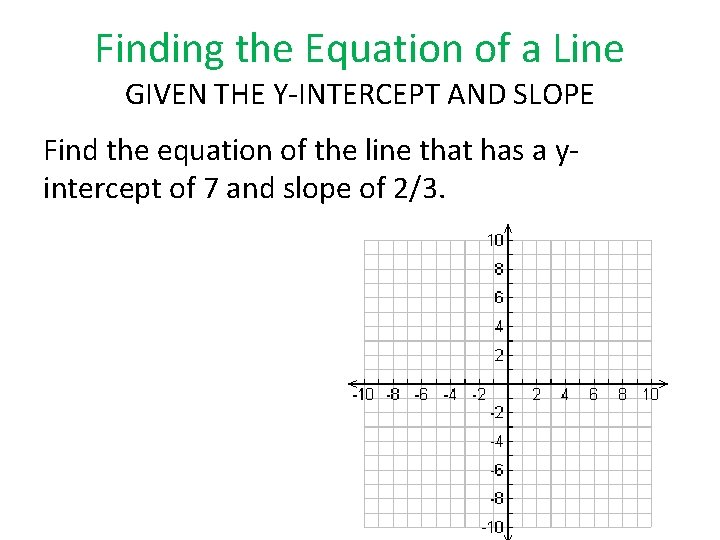
Finding the Equation of a Line GIVEN THE Y-INTERCEPT AND SLOPE Find the equation of the line that has a yintercept of 7 and slope of 2/3.

Finding the Equation of a Line GIVEN THE Y-INTERCEPT AND SLOPE Plug the slope in for m and the y-intercept in for b into slope-intercept form: Y = mx + b Example: Find the equation of the line that has a y-intercept of 7 and slope of 2/3. y = 2/3 x + 7

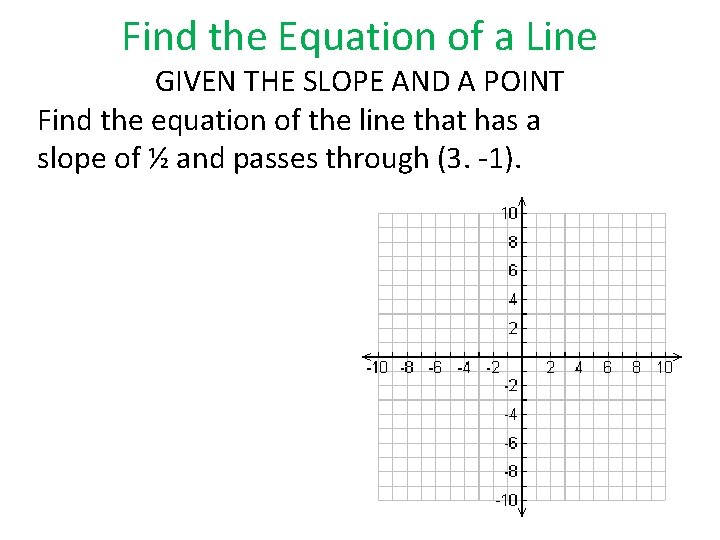
Find the Equation of a Line GIVEN THE SLOPE AND A POINT Find the equation of the line that has a slope of ½ and passes through (3. -1).

Finding the Equation of a Line GIVEN POINT AND SLOPE using point-slope form

Finding the Equation of a Line GIVEN POINT AND SLOPE using slope-intercept form 1. 2. 3. 4. Plug slope in for m in y = mx + b. Plug point in for x and y. Solve for b. Write equation in y = mx + b form. EXAMPLES

Find the Equation of a Line GIVEN TWO POINTS Find the equation of the line that passes through the points (2, -6) and (-3, 1).

Finding the Equation of a Line GIVEN 2 POINTS using point-slope form 1. Find the slope between the two points. 1. Plug the slope and a point into the point-slope form. EXAMPLES

Find the Equation of a Line GIVEN THE GRAPH Can use any of the previous three methods.

Parallel Lines Find the equation of a line that is parallel to 2 x – 3 y = 6 and passes through the point (2, -6). desmos

Parallel Lines Find the equation of a line that is parallel to y = 2 x – 4 and has an x – intercept of 4.

Perpendicular Lines Find the equation of the line that is perpendicular to y = 2 x – 4 and passes through the origin. DESMOS

Perpendicular Lines Find the equation of a line that is perpendicular to y = ¾ x – 1 and has a y-intercept of 8.

Real World Application of Slope We come across many examples of slope in everyday life. For example, a slope is in the pitch of a roof, the grade or incline of a road, or the slant of a ladder leaning on a wall.

Real World Application of Slope PROBLEM: Wheelchair ramps at building entrances must have a slope between 1/16 and 1/20. If the entrance to a new office building is 28 inches off the ground, how long does the wheelchair ramp need to be?